
- •Физика атома, атомного ядра и элементарных частиц
- •Выше (в лекции 7) были рассмотрены орбиталь- ный μl и собственный μs моменты
- •Сумма векторов L и S дает век-
- •На полуклассическом языке можно сказать, что векторы L и S, а вместе с
- •Найдем эту величину, для чего сложим проекции векторов μl и μs
- •Аналогично
- •Умножим числитель и знаменатель последней дро- би на j( j 1) :
- •Итак, эффективный магнитный момент атома равен:
- •Если поместить атом в магнитное поле то он будет вести себя как диполь
- •Сдругой стороны, ту же проекцию можно выра- зить с помощью косинуса угла между
- •Отсюда можно найти потенциальную энер- гию взаимодействия магнитного момента
- •Полученный результат легко обобщить на магнитный момент многоэлектронного атома. Как было отмечено выше,
- •При помощи векторной диаграммы аналогично тому, как это было сделано для одного электро-
- •Во внешнем магнитном поле B вектор μJ мо- жет ориентироваться относительно этого по-
- •Следствием принципа Паули является то, что у любой полностью заполненной (замкнутой) обо- лочки

Физика атома, атомного ядра и элементарных
ядра и элементарных  частиц
частиц
20 (2). Магнитный момент атома.

Выше (в лекции 7) были рассмотрены орбиталь- ный μl и собственный μs моменты электрона. Сумма этих моментов определяет полный маг- нитный момент атома. Найдем этот момент с помощью векторной диаграммы. Изображая на векторной диаграмме магнитные моменты необ- ходимо учесть, что гиромагнитное отношение для собственных моментов электрона вдвое  больше отношения для орбитальных моментов
больше отношения для орбитальных моментов  Вследствие этого направление вектора полного магнитного момента атома μ не совпадает с на- правлением полного механического момента J.
Вследствие этого направление вектора полного магнитного момента атома μ не совпадает с на- правлением полного механического момента J.
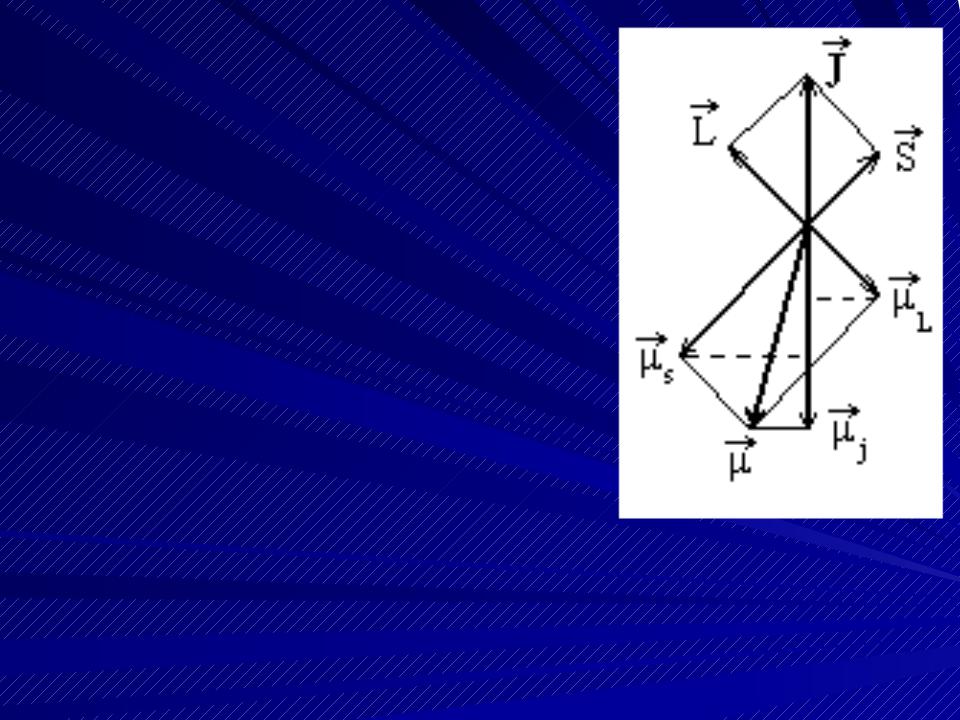
Сумма векторов L и S дает век-
тор J. Кроме механических мо- ментов, электрон имеет и маг- нитные моменты: орбитальный
μl и собственный μs, Направлен- ные противоположно соответст- вующим механическим момен- там. Если вектор μl изобразить
равным по длине вектору L, то в том же масштабе длина вектора
μs должна быть в два раза боль-
ше длины вектора S. Из-за этого, как сказано вы- ше, направление вектора полного магнитного мо- мента μ не совпадает с направлением J.

На полуклассическом языке можно сказать, что векторы L и S, а вместе с ними векто- ры μl и μs, прецессируют (вращаются) во- круг вектора J. Поэтому средние значения проекций, перпендикулярных к J, равны нулю (точнее говоря, эти проекции неоп- ределенны), а определенное значение имеет только одна проекция вектора μ  -проекция μj на направление вектора J.
-проекция μj на направление вектора J.  Эта величина называется эффективным полным магнитным моментом атома.
Эта величина называется эффективным полным магнитным моментом атома.
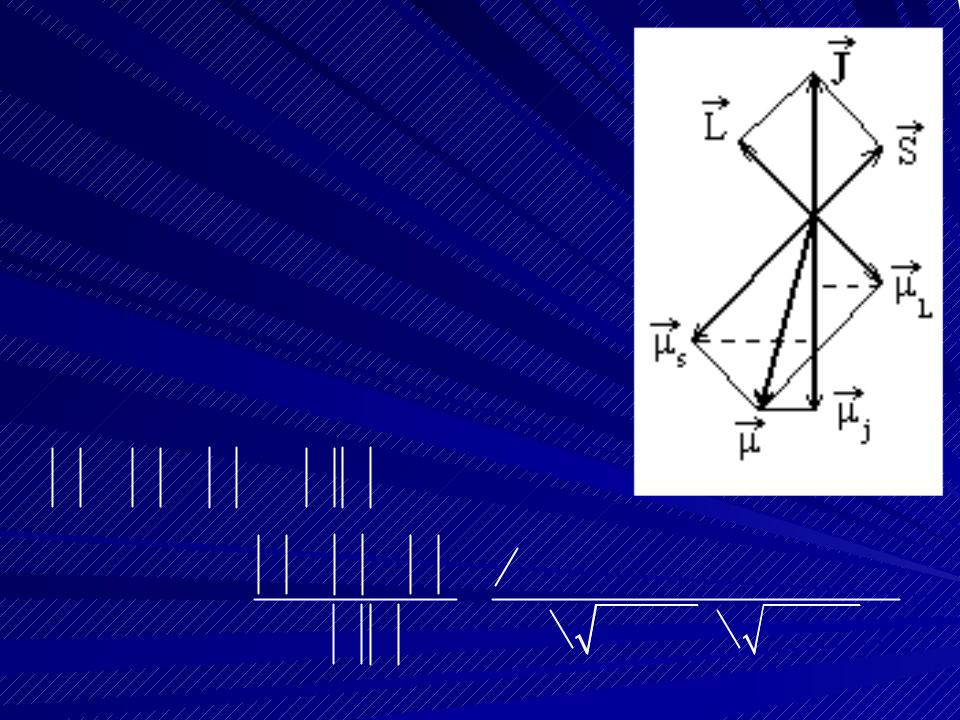
Найдем эту величину, для чего сложим проекции векторов μl и μs
на направление J: |
r |
r |
|
|
r r |
|
|
||
j l cos L, J |
s cos S |
, J |
||
Для определения косинусов вос- пользуемся теоремой косинусов из элементарной геометрии
r |
2 |
|
r 2 |
|
r 2 |
2 |
r |
r |
cos |
r |
r |
|
|
|
|
|
|
|
|||
L |
|
J |
|
S |
J |
S |
S |
, J |
|
|
|
|
|
|
|||||||
|
|
|
|
r r |
|
r 2 |
|
r 2 |
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
S |
L |
|
|
|
2 |
|
|
||||||||
cos |
S, J |
|
|
r |
r |
|
h |
j( j |
|
1) |
|
s(s 1) |
l(l |
1) . |
|||||||
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
J S |
|
|
|
|
2 h j( j 1) h s(s 1) |
||||||||

Аналогично |
|
|
r |
r |
|
|
r r |
|
|
|
|
||||
r 2 |
r 2 |
|
r |
2 |
2 |
|
cos |
|
|
|
|||||
S |
J |
|
L |
|
L |
J |
|
L, J |
|
|
|||||
|
|
r r |
|
|
r 2 |
|
r |
2 |
r 2 |
h 2 |
|
j( j 1) l(l 1) s(s 1) |
. |
||
cos |
|
J |
L |
|
S |
|
|||||||||
L, J |
|
2 |
r |
|
r |
|
|
||||||||
|
|
|
|
|
|
|
J L |
|
|
2 h j( j 1) h l(l 1) |
|
||||
Поэтому |
l(l 1) j( j 1) l(l 1) s(s 1) |
|
j 0 |
||
|
|
2 j( j 1) l(l 1) |
2 0 |
s(s 1) j( j 1) s(s 1) l(l 1) |
|
|
|
2 j( j 1) s(s 1) |
0 |
3 j( j 1) s(s 1) l(l 1) |
|
|
|
2 j( j 1) |

Умножим числитель и знаменатель последней дро- би на j( j 1) :
|
j |
|
0 |
j( j 1) |
1 |
j( j 1) s(s 1) l(l 1) |
|
|
|
|
|
2 j( j 1) |
|
||
|
|
|
|
|
|
|
Обозначим выражение, стоящее в фигурных скоб-
ках: |
|
g 1 j( j 1) s(s 1) l(l 1) |
(20.1) |
2 j( j 1) |
|
Эта величина называется множителем (фактором) Ланде (Lande A.) и определяет гиромагнитное отно- шение для эффективного полного момента атома.

Итак, эффективный магнитный момент атома равен:
j 0 g |
j( j 1) |
(20.2) |
|
|
а гиромагнитное отношение для μj :
j |
0 g |
j( j 1) 0 g |
e g |
(20.3) |
||
J |
h j( j 1) |
h |
2m0 |
|||
|
||||||

Если поместить атом в магнитное поле то он будет вести себя как диполь с моментом μj, причем ори-
ентация этого момента будет определяться проек- |
||
циями вектора J на направление магнитного поля: |
||
|
r |
r |
jB j cos J |
, B |
|
r |
r |
|
Чтобы найти cos J |
, B воспользуемся формулами |
|
(17.5) и (17.6). Согласно формуле (17.5), проекция
момента J на направление B равна
JB mj h ,
где магнитное внутреннее квантовое число прини-
мает значения:
mj j, j 1, j 2, ..., j

Сдругой стороны, ту же проекцию можно выра- зить с помощью косинуса угла между вектора-
r r
1)cos J , BJB j( jми J и B: h
|
r |
r |
mj |
отсюда |
cos J |
, B |
j( j 1) |
|
|
Таким образом, проекция эффективного магнит- ного момента атома на направление внешнего
магнитного поля равна: |
|
mj |
|
||
|
r |
r |
j |
|
|
jB j cos J |
, B |
j( j 1) |
|||
|
|
|
|
|
|
|
|
|
mj |
|
(20.4) |
0 g |
j( j 1) |
j( j 1) |
0 gmj |
||
|
|
|
|
|
|
