
Шпаргалки / Шпаргалки (Бардушкин) / Шпаргалки в Word / шпора1
.doc|
1.Предмет теории вероятностей Теория вероятностей – раздел математики, изучающий закономерности случайных явлений. Разница между закономерными и случайными событиями. Закономерное событие – это событие, которое всегда осуществляется, как только создаются определённые условия. Закономерное явление – это система закономерных событий. Случайные события – это события, которые при одних и тех же условиях иногда происходят, а иногда нет. Однако случайные события подчиняются некоторым закономерностям, которые называются вероятностными закономерностями, при этом надо условится, что мы будем иметь дело не со всякими случайными событиями, а с массовыми, то есть будем предполагать, что в принципе можно создать много раз одни и те же условия, при каждом из которых могут произойти или нет некоторые случайные события. Пусть при осуществлении некоторых условий (N раз), случайное событие A, будет осуществляться N(А) раз. Число
N(А)
– называется частотой событий A,
а отношение
Если N велико, относительная частота для случайных массовых событий обладает свойством устойчивости. Пример.
Относительная частота колеблется около определенного числа, которое характеризует данное случайное событие. Р(А) – вероятность события А. Примеры. 1)Пусть случайное событие A – выпадение герба при одном подбрасывании симметричной однородной монеты. Р(А)
=
1)Статистика рождений показывает, что мальчиков рождается несколько больше, чем девочек. Доля рождения мальчиков 0,51-0,52. Р(А) = 0,51; 0,51 – вероятность рождения мальчиков. События Достоверное
событие
– событие, которое всегда происходит
( Невозможное событие – событие, которое не происходит никогда (). Событие
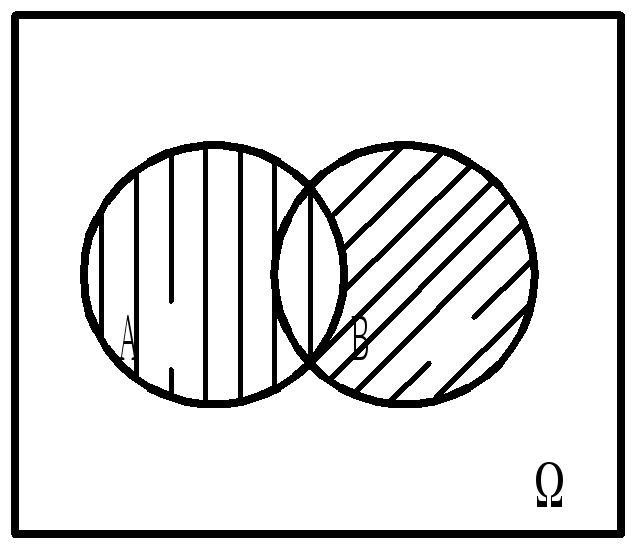
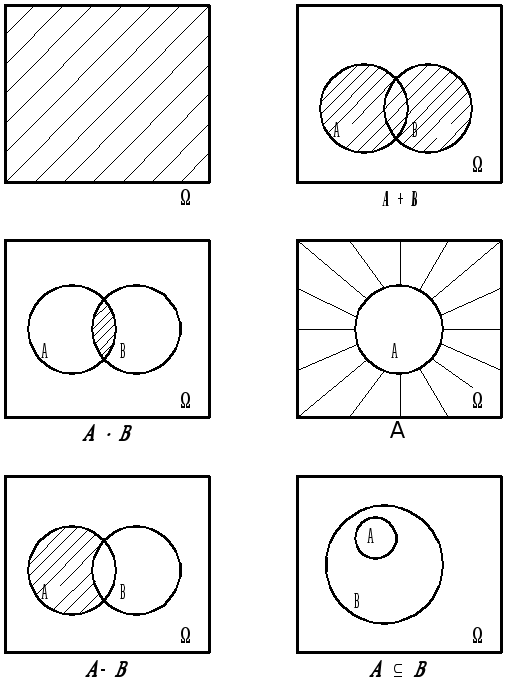
Суммой событий A и B называется событие A+B, которое происходит тогда и только тогда, когда происходит или A, или B, или оба вместе. Произведением событий A и B называется событие AB, которое происходит тогда и только тогда, когда происходят A и B вместе. Разностью событий A и B называется событие A-B, которое происходит тогда и только тогда, когда происходит A и не происходит B. События A и B несовместны, если AB=. Событие A влечет за собой событие B, если из наступления события A следует наступление события B (A B). События A и B называются равносильными A=B, если выполняются одновременно два включения
Пример. Бросается игральная кость. A = {выпадает четное число очков} B = {выпало число очков, не большее трех} Решение. Выпало число очков отличное от 5 (A+B). Выпала 2 (AB). Выпало число очков равное 4 или 6 (A-B). Выпадает нечетное число очков (Ā).
5,6..Размещения и сочетания Набор
элементов xi1,
xi2,
…, xin
из множества
Выборка называется упорядоченной, если порядок следования элементов в ней задан. Замечание Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными. Если порядок следования элементов не является существенным, то выборка называется неупорядоченной. В выборках могут допускаться или не допускаться повторения элементов. Упорядоченная <n, r>-выборка, в которой элементы могут повторяться, называется <n, r>-размещением с повторениями. Упорядоченная <n, r>-выборка элементы, которой попарно различны, называется <n, r>-размещением без повторений (<n, r>-размещением). Замечание <n,
n>-размещения
без повторений называются перестанов-ками
множества
Неупорядоченная <n, r>-выборка, в которой элементы могут повторяться, называется <n, r>-сочетанием с повторениями. Неупорядоченная <n, r>-выборка элементы, которой попарно различны, называется <n, r>-сочетанием без повторений (<n, r>-сочетанием). Замечание Любое <n, r>-сочетание можно рассматривать, как r-элемент-ное подмножество n-элементного множества. Теорема 1
Доказательство: Каждое <n,r>-размещение с повторениями является упорядоченной последовательностью длины r Причем каждый элемент этой последовательности может быть выбран n-способами. По правилу произведения получаем
Теорема 2.
Доказательство: Каждое <n,r>-размещение без повторений является упорядоченной последовательностью длины r. По правилу произведения получаем
Теорема 3.
Доказательство: Каждое <r,r>-сочетание без повторений можно упорядочить r!-способами. Объединение получаемых таким образом попарно непересекающихся множеств <n,r>-размещений без повторений для всевозможных <n,r>-сочетаний без повторений, даст все <n,r>-размещения без повторений.
Теорема 4.
7. Геометрические вероятности Геометрические вероятности – класс моделей вероятностных пространств, дающий геометрические вероятности. Пусть Ω={ω} – ограниченное множество n-мерного евклидова пространства с конечным n-мерным объёмом. Событиями назовём подмножества Ω, для которых можно определить n-мерный объём. Для любого A A положим
, где |V|-n-мерный объем множества V A. Это вероятностное пространство служит моделью задач, в которых частица случайно бросается в область Ω. Предполагается, что положение частицы равномерно распределено на множестве Ω, т. е. вероятность попадания частицы в подмножество A пропорциональна n-мерному объёму этой области. Замечание. В классе конечных вероятностных пространств в систему A входили все подмножества Ω. При геометрическом определении вероятности в качестве A уже нельзя взять все подмножества Ω, так как некоторые из них не имеют n-мерного объёма. Примеры 1. Стержень разламывается на две части в случайной точке, равномерно распределённой по длине стержня. Найти вероятность того, что длина меньшего обломка окажется не больше трети длины всего стержня.
Обозначим за x расстояние от фиксированного конца стержня до точки излома.
2.Задача Бюффона. Плоскость расчерчена па-раллельными прямыми, расстоя-ние между которыми равно a. На плоскость наудачу брошена игла длины l (l<a). Найти вероятность того, что игла пересечет какую-либо прямую. Решение.
Пусть y
– расстояние от центра иглы до
ближайшей прямой
|
2. Вероятностное пространство Тройка (, A, P), где – это пространство элементарных событий; A – -алгебра подмножеств , называемых событиями; P – числовая функция, определенная на событиях и называемая вероятностью. P называется вероятностным пространством, если выполнены следующие аксиомы: A1. P(A) 0, A A. A2. P() = 1 (нормированность P). A3. P(A+B)=P(A) + P(B), если AB= (аддитивность). A4. Для любой убывающей последовательности
событий из A такой, что
имеет место
равенство
Замечания. Аксиомы 3, 4 можно заменить одной аксиомой -адди-тивности. 3*.
Если события An
в последовательности A1,
A2,
… попарно
несовместны,
то
Из этих аксиом вытекают следующие свойства. Свойства вероятностей
Доказательство: Разобьем событие B в сумму несовместных событий B=A+(B-A) A(B-A)= P(B) = P(A+(B-A))=P(A)+P(B-A) (по аксиоме 3) P(B-A)=P(B) - P(A) .
Доказательство: Доказательство следует из 1 свойства и аксиомы 1. P(A) + P(B-A) = P(B) P(B-A) 0, следовательно P(A) P(B) .
Доказательство: A P(A) P() P() = 1 (по аксиоме 2) P(A) 0, A A (по аксиоме 1) .
Доказательство: A+ Ā = A Ā = Тогда по аксиоме 3 и аксиоме 2 получаем P(A+ Ā) = P(), P(A) + P(Ā) = P(), P(A) +P(Ā) = 1 P(Ā) = 1 - P(A) .
Доказательство: + = Тогда по аксиоме 3 и 2 получаем, P() + P() = P() P() + 1 = 1, P() = 0 .
A, B A P(A+B) = P(A) + P(B) – P(AB)
Доказательство:
A + B = A + (B - AB), A(B - AB) = P(A+B) = P(A) + P(B - AB), но AB B следовательно по первому свойству (вероятность от разности равна разности вероятностей). P(A+B) = P(A) + P(B) – P(AB) .
3.Конечное вероятностное пространство. Классическое определение вероятности. Рассмотрим случай конечного вероятностного пространства. В этом случае состоит из конечного числа элементарных событий . = {} A
– алгебра всех подмножеств
(ввиду конечности вероятностного
пространства алгебра автоматически
является -алгеброй),
тогда вероятность
Пусть
заданы неотрицательные числа
Очевидно,
что так определенная вероятность
вместе
Обозначим
через
Частным
случаем определения вероятности по
формуле (*) будет так называемое
классическое определение вероятностей,
когда все
Замечание Модель вероятностного пространства, приводящая к классическому определению вероятностей, когда элементарные события обладают свойствами «симметрии». Пример. Бросается кубик на стол. 1 = {выпадает 1} 2 = {выпадает 2} – свойства симметрии
9.Формула полной вероятности Система
событий
Теорема (Формула полной вероятности) Если
Доказательство:
Пример. В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность события B={второй вынутый шар белый}. A = {первый шар белый}
Решение A A
+
Пример показывает, что при правильно организованной жеребьевке шансы будут равны.
10.Формулы Байеса
Теорема.
Если
Доказательство: По теореме умножения:
Формулы Байеса
можно интерпретировать следующим
образом: назовём
Формулы Байеса позволяют по априорным и условным вероятностям вычислить апостериорные вероятности гипотез. Пример. Детали, изготовленные цехом завода, попадают к одному из двух контролёров для проверки на стандартность. Вероятность того, что деталь попадёт к первому контролёру – 0,6; ко второму контролёру, соответственно, – 0,4. Вероятность того, что годная деталь будет признана стандартной, для первого контролёра – 0,9; для второго – 0,98. Годная деталь была признана стандартной. Найти вероятность того, что её проверил первый контролёр. Решение.
|
4.Основные правила комбиноторики. Комбинаторика – это наука о том, сколько различных комбинаций удовлетворяющих условиям можно составить на элементах конечного множества. Комбинаторные схемы
Правило суммы
Объект
Правило произведения Если
объект
Тогда
выбор упорядоченной пары
Доказательство: Воспользуемся правилом суммы.
Множество
пар
В общем случае правило произведения формируется следующим образом: Если
объект
Доказательство проводится методом математической индукции.
Диаграммы Эйлера
В теории вероятностей очень распространенным является подход, в котором событие определяется через неопределяемые понятия элементарного события. Наиболее употребительная теоретико-вероятностная модель – урновая модель. Пусть
имеется урна с N
одинаковыми шарами. Испытание состоит
в том, что из урны случайно выбирается
один шар.
n – множество шаров в урне. Если мы из урны выбираем шар i A, где A – некоторое подмножество , то мы будем говорить, что произошло событие A. Если i A, где A – некоторое подмножество , то мы будем говорить, что событие A не произошло. = {} – пространство элементарных событий. – элементарные события. Замечания. Операции суммы и произведения событий можно распространить на конечные и бесконечные множества событий.
В общем случае бесконечного пространства , мы будем брать не все подмножества в отличие от конечного, а лишь некоторые классы этих подмножеств, называемые алгебрами и - алгебрами этих подмножеств. Назовем класс A подмножеств пространств алгеброй множеств, если 1) A , A. 2) из A A Ā A. 3) из A,B A A+B A, AB A. Алгебра
событий A
называется -алгеброй
или борелевской алгеброй, если из
того, что
11. Независимость событий
Если события A
и B
таковы, что
Определение.
Событие A
не зависит от события B,
если
Если
потребовать условия
Понятие того, что одно событие зависит от другого, симметрично. Замечание. Из теоремы умножения:
Это приводит к определению.
Определение.
События A
и B
называются
независимыми,
если вероятность произведения событий
равна произведению вероятностей
событий
Независимость событий в совокупности.
События
В противном случае — события зависимы.
Замечание.Из
определения независимости событий
в совокупности следует, что события
любого подмножества
Пример.
Имеются 4 числа: 2, 3, 5, 30. Наудачу
выбирается одно число. Вероятность
этого события – 0,25.
Решение.
Совокупная независимость более сильное свойство, нежели попарная независимость.
Теорема.
Если события
8.Условные вероятности; теорема умножения
N – число испытаний; A, B, AB – события; N(A), N(B), N(AB) – частоты событий;
Если все относительные частоты событий устойчивы, тогда условная относительная частота тоже устойчива. Пусть P(B)>0.
Условной
вероятностью
P(A|B)
события A
при условии, что событие B
произошло, называется отношение
P(A|B) = PB(A) (встречается в литературе). Теорема умножения
Если P(A)>0,
P(B)>0,
а P(A|B),
то вероятность произведения
Доказательство: Доказательство следует из определения. Пример 1 способ. В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность того, что оба шара будут белыми. A = {1 вынутый шар белый} B = {2 вынутый шар белый} AB = {оба шара белых}
2 способ.
Следствие.
Пусть события
Доказательство:Доказательство проводится методом математической индукции.
|

 .
.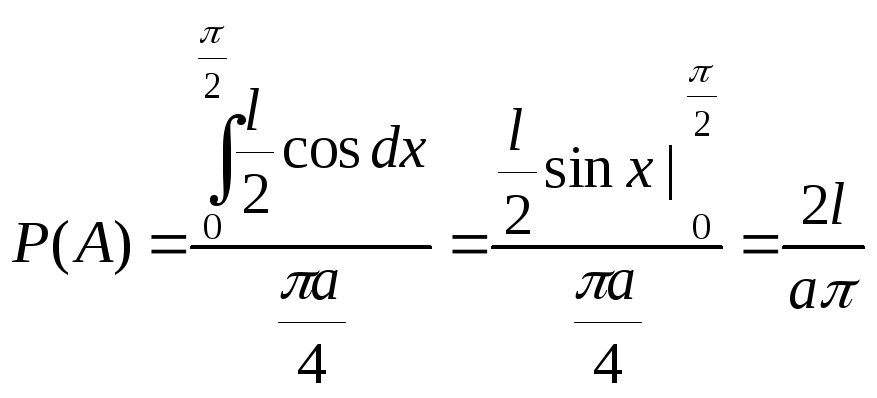 .
.
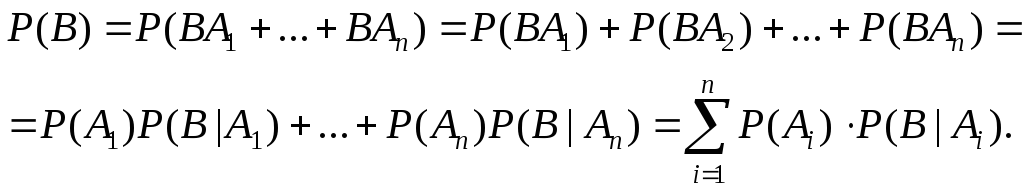
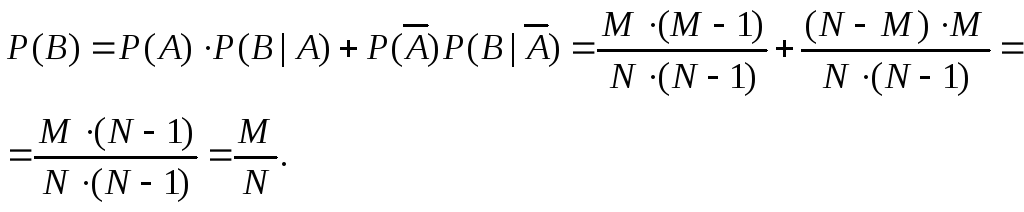
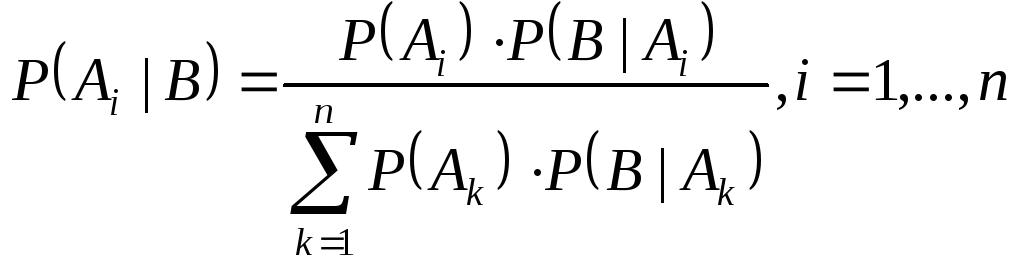
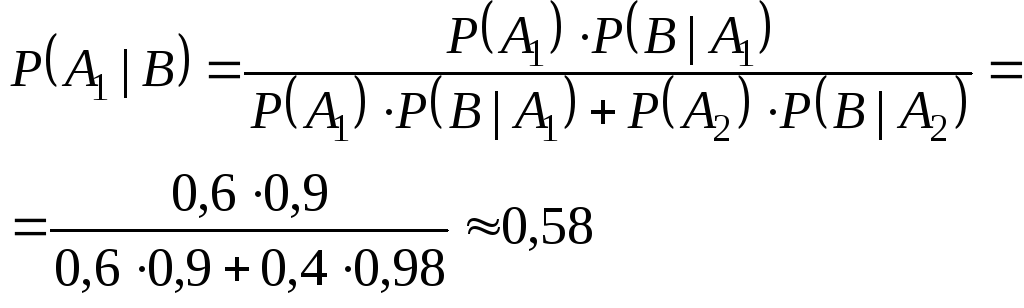

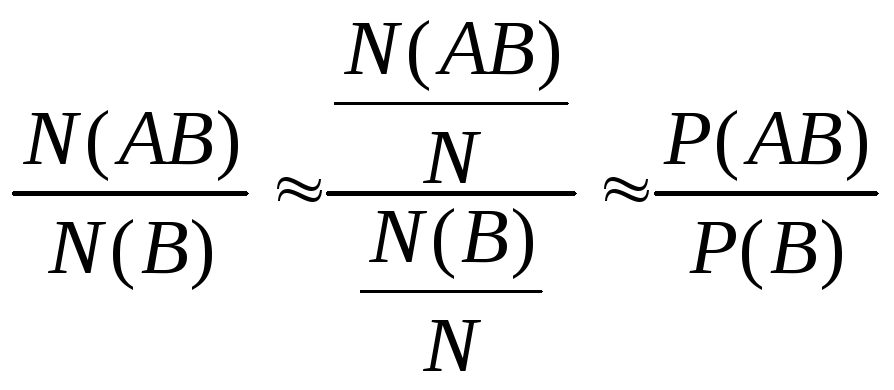 .
.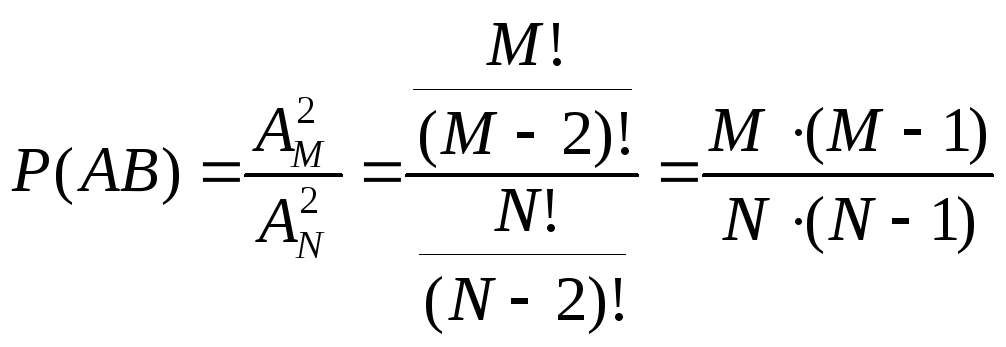 .
.