Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 19,20

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 19

Глава 10

Элементы математической статистики

§ 1. Задачи математической статистики. Установления закономерностей, которым подчинены массовые случайные явления основано на изучении методами теории вероятностей статистических данных (результатов наблюдений

1. Задача математической статистики

Указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально составленных экспериментов.

2. Задача математической статистики

1) Разработать методы анализа статистических данных в зависимости от целей исследования:

• оценка неизвестной вероятности событий;

• оценка неизвестной функции распределения;

• оценка параметров распределения, вид которого известен;

• оценка зависимости СВ от одной или нескольких других СВ.

2) Проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения вид, которого известен.

Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности.

§ 2. Выборка и способы ее представления

Математическая статистика позволяет получить обоснованные выводы о параметрах, видах распределений и других свойствах СВ о конечной совокупности наблюдений над этими величинами.

Выборка понимается следующим образом. Пусть СВ Х наблюдается на каком либо эксперименте, повторим этот эксперимент n раз при одинаковых условиях. Получаем , где каждая – СВ соответствующая j-му эксперименту. Очевидно, что – независимые в совокупности СВ, причем каждая из этих СВ имеет один и тот же закон распределения, что и СВ Х.

Определение.

Закон распределения СВ Х называется распределением генеральной совокупности.

СВ вектор называется выборочным вектором, а конкретные числа , получаемые на практике при n кратном повторении эксперимента в неизменных условиях представляет собой реализацию выборочного вектора и называются выборкой объема n.

Что такое вариационный ряд, размах выборки, статистический ряд, группированный статистический ряд, частоты, относительные частоты, накопленные частоты, относительные накопленные частоты, всевозможные полигоны и гистограммы, а также, что такое эмпирическая функция распределения изучили самостоятельно.

§ 3. Числовые характеристики выборки

Пусть выборка объема n из генеральной совокупности с функцией распределения .

Рассмотрим выборочное распределение, т.е. распределение дискретной СВ, принимающей эти значения с вероятностями, равными . Соответственно числовые характеристики этого выборочного распределения называют выборочными (эмпирическими) числовыми характеристиками.

Замечание.

Выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности.

“~” – при обозначении этих числовых характеристик.

.

.

.

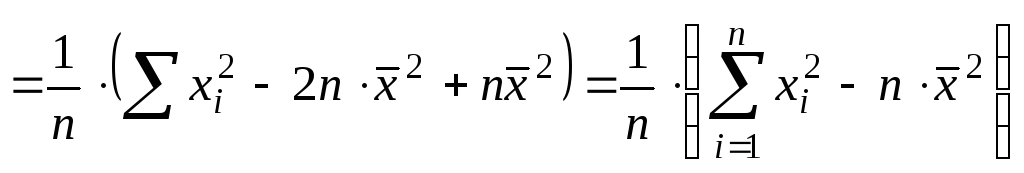– унимодального, т.е. одновершинного распределения называется элемент выборки, встречающийся с наибольшей частотой.

Выборочной медианой называется , которое делит вариационный ряд на две части, содержащие равное число элементов.

Если n – нечетное число, т.е. n = 2l+1, то .

Если n – четное число, т.е. n = 2l, то .

Можно доказать, что выборочные начальные и центральные моменты порядка s для негруппированных выборок объема и определяются по следующим формулам

.

Форма распределения СВ характеризуется выборочными коэффициентами асимметрии и эксцесса.

.

§ 4. Статистическое описание и вычисление оценок параметров распределения системы двух СВ

Пусть исход некоторого эксперимента описывается двумя СВ (X; Y).

Предварительное представление о зависимости между X и Y можно получить, нанося элементы двумерной выборки , в виде точек на плоскость с выбранной системой координат. Такое представление называется диаграммой рассеяния.

Определение.

Распределением двумерной выборки называется распределение двумерного дискретного СВ случайного вектора, принимающего значения с вероятностями .

Выборочные числовые характеристики вычисляются как соответствующие числовые характеристики двумерного дискретного случайного вектора. Если объем выборки небольшой, то тогда вычисления проводятся в следующей последовательности:

1. .

Контроль .

2. Суммы квадратов отклонений от среднего и произведения отклонений от среднего

.

3.

. .

§ 5. Линии регрессии

Для СВ X и Y.

Регрессией Y на X называется условное МО .

используется для предсказания значения СВ Y по фиксированному значению СВ X.

Если , то говорят о линейной регрессии Y на X.

– прямая регрессии.

Оценки параметров линейной регрессии по выборке , где , можно получить, используя МНК из условия минимума суммы

.

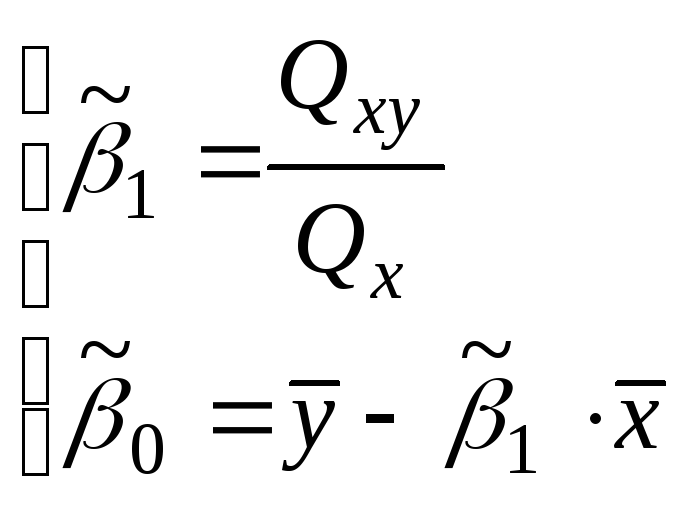– выборочные коэффициенты регрессии.

.

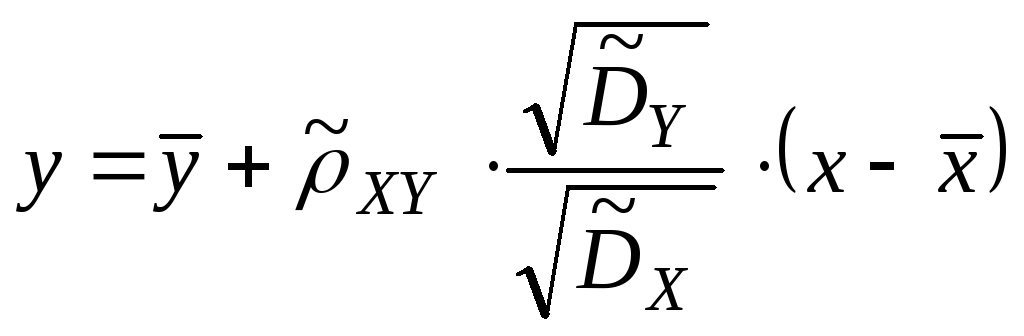Выборочная линейная регрессия Y на X. Аналогично рассматривается X на Y.

.

Обе прямые регрессий пересекаются в точке с координатами .

Угол между этими двумя прямыми уменьшается при увеличении коэффициента корреляции.

При обе прямые совпадают.

Замечание.

Прямые и должны быть различны.

Лекция № 20

§ 6. Оценки параметров распределения

Пусть неизвестная функция генеральной совокупности зависит от некоторого параметра . Нужно по наблюдениям оценить параметр.

Для построения оценок используются статистики – функции от выборочных значений.

Примеры статистик.

.

Эта оценка

.

Будет рассматриваться, как приближенное значение параметра .

Замечание.

Как правило, для оценки параметра можно использовать несколько статистик, получая при этом различные значения параметра .

Как измерить «близость» оценки к истинному значению ? Как определить качество оценки?

Комментарий:

Качество оценки определяется не по одной конкретной выборке, а по всему мыслимому набору конкретных выборок, т.е. по случайному выборочному вектору , поэтому для установления качества полученных оценок моментов , следует во всех этих формулах заменить конкретные выборочные значения на СВ X_i.

.

Качество оценки устанавливают, проверяя, выполняются ли следующие три свойства (требования).

Требования, предъявляемые к точечным оценкам:

1. Несмещенность, т.е. .

Это свойство желательно, но не обязательно. Часто полученная оценка бывает существенной, но ее можно поправить так, что она станет несмещенной.

Иногда оценка бывает смещенной, но асимптотически несмещенной, т.е. .

2. Состоятельность, т.е. .

Это свойство является обязательным. Несостоятельные оценки не используются.

3. Эффективность.

а) Если оценки и – несмещенные, то и .

Если , то оценка более эффективна, чем .

б) Если оценки и – смещенные, тогда и .

Если , то оценка более эффективная, чем .

Где – средний квадрат отклонения оценки.

Рассмотрим использование этих свойств на примерах выбора оценок МО и дисперсии:

1. Выборочное среднее

является несмещенной и состоятельной оценкой МО генеральной совокупности , причем каждое X_i совпадает с m и ².

а) Несмещенность.

По определению выборочного вектора

, причем X_i – независимые в совокупности СВ, тогда вычислим

;

.

.

б) Состоятельность

Воспользуемся неравенством Чебышева:

Применим это неравенство к

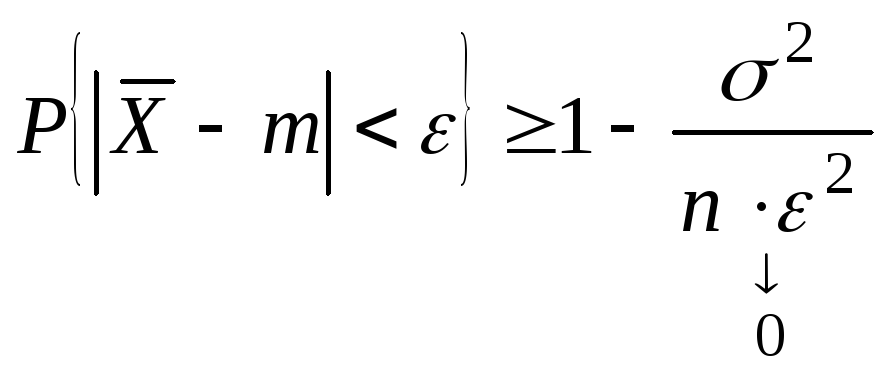
При n

, что и доказывает состоятельность .

2. Выборочная дисперсия

Докажем, что выборочная дисперсия является смещенной оценкой для дисперсии генеральной совокупности.

Выполним следующие преобразования

;

.

Найдем МО для дисперсии:

.

.

МО не совпадает с ², а отличается на – смещение.

Таким образом эта оценка занимает в среднем истинное значение дисперсии на величину , правда это смещение сходит на нет при n  .

Чтобы устранить это смещение надо «исправить» дисперсию.

.

Можно доказать, что статистика S² является и состоятельной оценкой для дисперсии генеральной совокупности.

Замечание.

К сожалению, на практике при оценке параметров не всегда оказывается возможным одновременное выполнение требований: несмещенности, эффективности и состоятельности.

§ 7. Интервальные оценки. Доверительный интервал. Доверительная вероятность

В ряде задач требуется не только найти для параметра подходящую оценку , но и указать к каким ошибкам может привести замена параметра его оценкой , т.е. требуется оценить точность и надежность оценки.

Для определения точности оценки в статистике пользуются доверительными интервалами.

Для определения надежности оценки в статистике пользуются доверительной вероятностью.

Определение.

Доверительным интервалом для параметра называется интервал , содержащий истинное значение параметра с заданной вероятностью .

.

Определение.

Число называется доверительной вероятностью, а значение  – уровнем значимости.

Замечание.

Нижняя и верхняя граница доверительного интервала определяется по результатам наблюдений и следовательно является СВ. Поэтому так и говорят, что доверительный интервал «накрывает» оцениваемый параметр с вероятностью .

Выбор доверительной вероятности каждый раз определяется конкретной постановкой задачи. Обычно р = 0,9; р = 0,95; р = 0,99.

Часто применяют односторонние доверительные интервалы (левосторонний), (правосторонний).