Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци6
.docЛекция 6
§ 2.4. Основные дисперсные распределения и их числовые характеристики.
Ключевым понятием является "момент распределения"
|
Момент распределения |
|
|
Начальный момент S-го порядка
S= pk=P{X=xk}, xk Ex
S=0,1,… 0=1(неинтересно)
|
Центральный момент S-го порядка Ms= pk=p{X=xk}, xk Ex
S=0,1,…M0=1 (неинтересно) |
,
Определение:
mx=1=
называется
математическим ожиданием (mx
- метка
величины). Это среднее значение случайной
величины Х
по распределению
(пример: формула центра тяжести). Часто
mx
называют
"центром распределения".
Определение:
Dx=M2=
называется
дисперсией
- степень разброса случайной величины.
Определение:
Величина
ax=
называется
асимметрией,
где
—
среднеквадратическое
отклонение (
— эталон разброса). Если
=0,
то такое
ожидание называется симметричным.
Определение:
ex=
-3
называется
эксцессом.
Преобразуем формулу (1):
Dx=
=
=
-
+
=
=
-
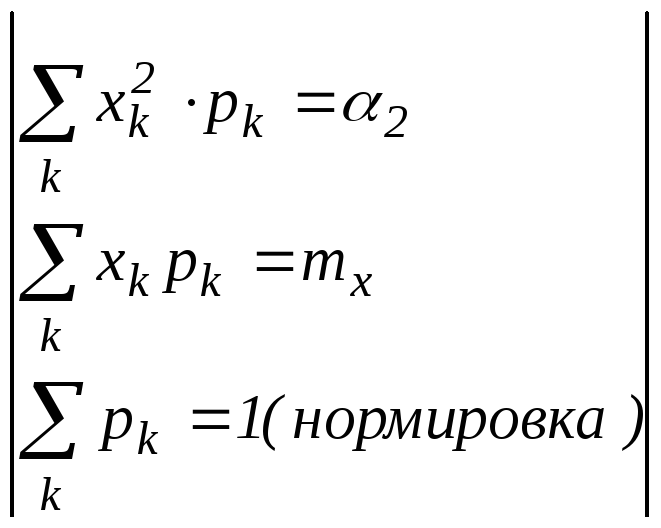Dx=
-
(2)
I. Равномерное распределение (дискретное)
ХR(n), n- число дискретов. Таблица распределения в этом случае имеет вид:
|
Х |
х1 |
х2 |
… |
хn |
|
P |
|
|
… |
|
mx=
-среднее
арифметическое.
Dx=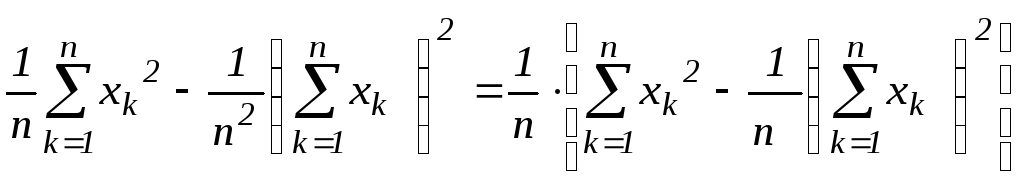
II. Биномиальное распределение
Пусть ХB(n,p), т.е. спектр возможных значений Ex={0,1,2,…,n}
P{X=k}=Pn,k(p)=
,
k
Ex
Найдем mx и Dx
mx=
(*)
Эту сумму можно свернуть двумя способами:
1) С использованием бинома Ньютона
/*Формула бинома Ньютона
(3) (q+p)n=
,
q и p - произвольные действительные
числа.
Если q+p=1, то бином Ньютона дает нормировку и возможность использовать различные операции */
Выражение (*) отличается от (3) на множитель k, поэтому (3) надо продифференцировать по k и умножить на p:
P[(q+p)n]'
=mx=p(n(q+p)n-1)(q+p)=1=np
mx=mp
Для вычисления
дисперсии по формуле (2) находим
:
=
[(q+p)n]'=[n(q+p)n-1]=
p[np(q+p)n-1]'p=
=pn((q+p)n-1+(n-1)p(q+p)n-2)=
(т.к. q+p=1) =np(1+np-p)=np(q+np)=|q=1-p|=n2p2+npq
Dx=
-
=
n2p2+npq-
n2p2=npq
Dx=npq
2) С помощью производящей функции
/* Производящая функция для биномиального распределения:
(x)=(q+px)n=
,
где Pn,k
- биномиальные
вероятности.
mx= '(x)|x=1 =n(q+px)n-1p=np(q+1-q)n-1=np
=[x
'(x)]'x=1=np+xnp(n-1)p(q+px)n-2=np(1+np-p)=np(np+q)
Dx=(np)2+npq-(np)2=npq
Dx=npq
III. Распределение Пуассона
Определение:
Говорят, что Х
подчиняется
распределению Пуассона с параметром
>0
(кратко
пишут: XPu()),
если множество
возможных значений Ex=
={0,1,2,…},
а соответствующие
вероятности вычисляются так:
Pk=P{X=k}=
(4)
Вычислим mx и Dx.
Нормировка:
=
=
=1
mx=
=
=
=
=
=
=
=
=
=
=
=
+
=
+
=
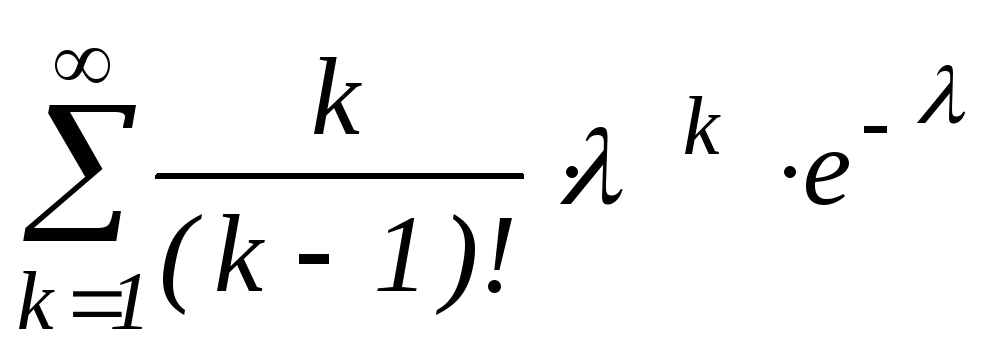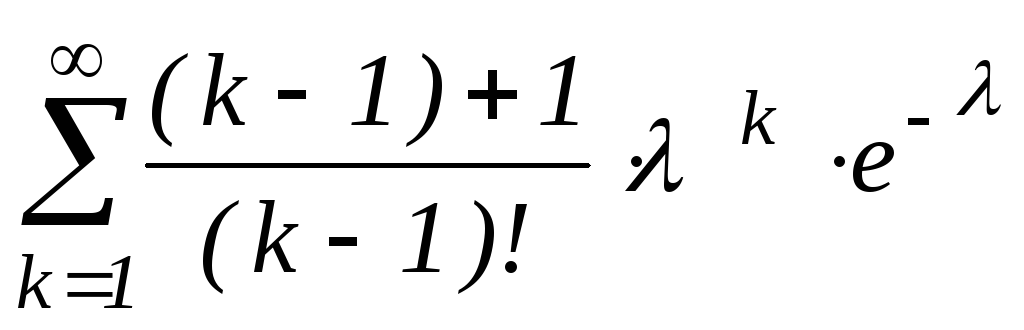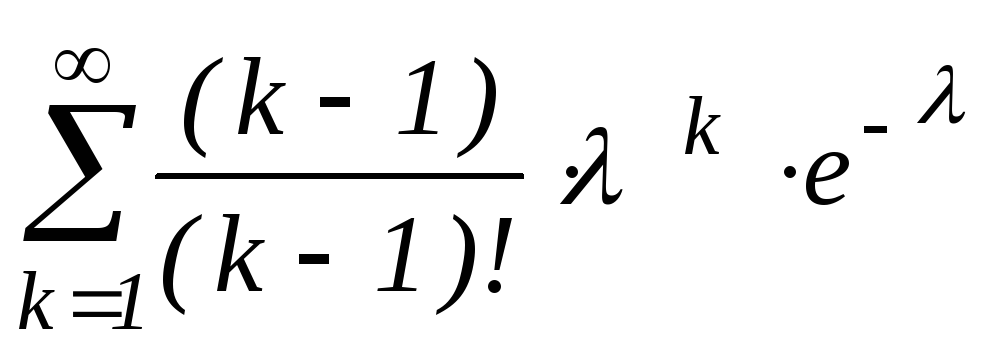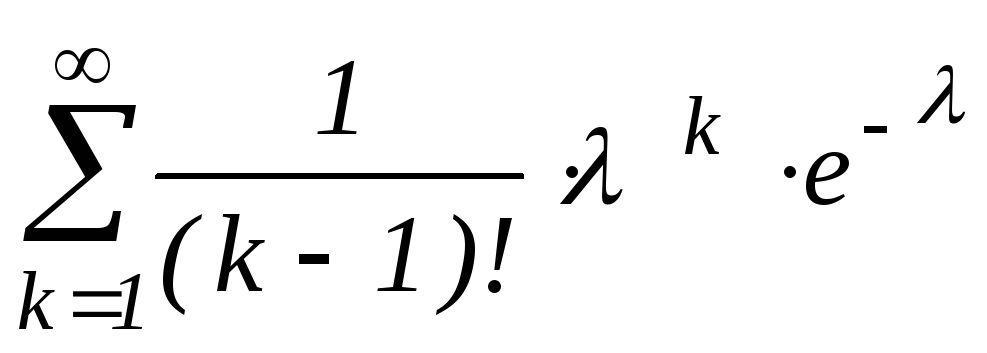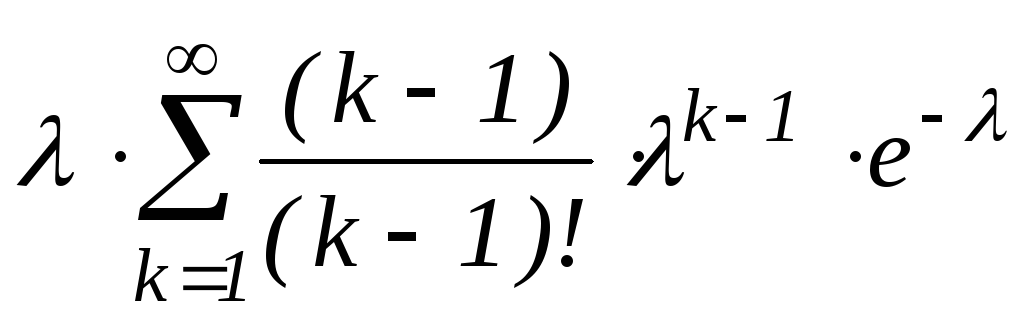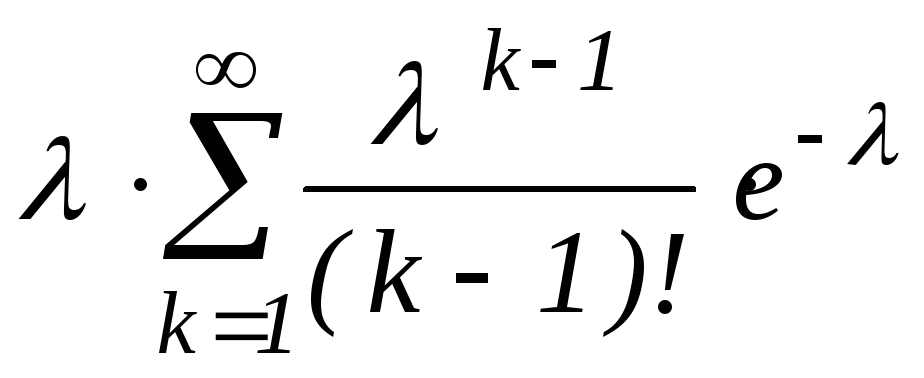Dx=
Dx=mx=
X~Pu() mx=Dx=
X~B(n,p) mx=np, Dx=npq
Распределение Пуассона описывает:
- число атомов, распавшихся в единицу времени (радиоактивный распад)
- число независимых вызовов на АТС в единицу времени
Теорема 6.1. Пусть
X~B(n,p),
причем положим =np,
т.е.
и устремим n
(
- некоторая константа) при этом
= const,
Pn,k(
)=
=
=
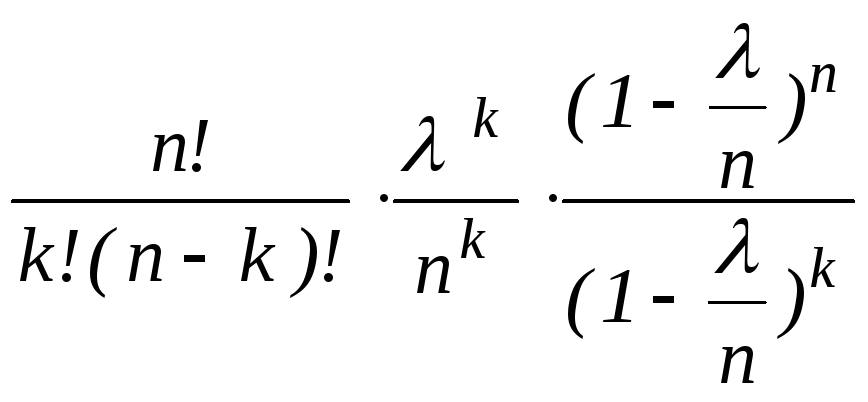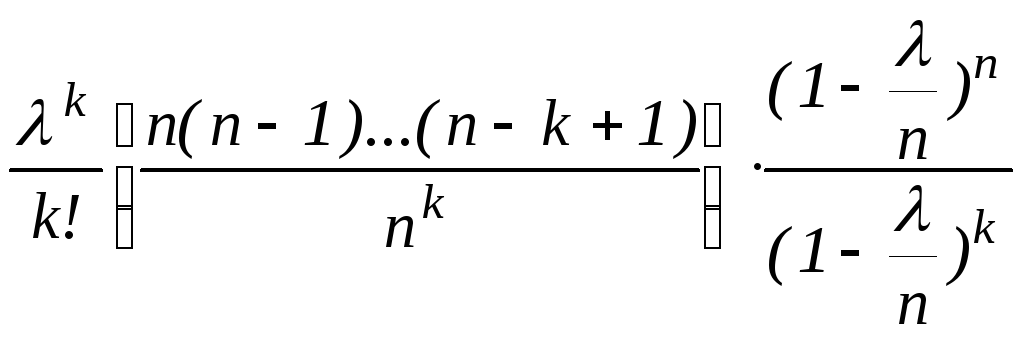
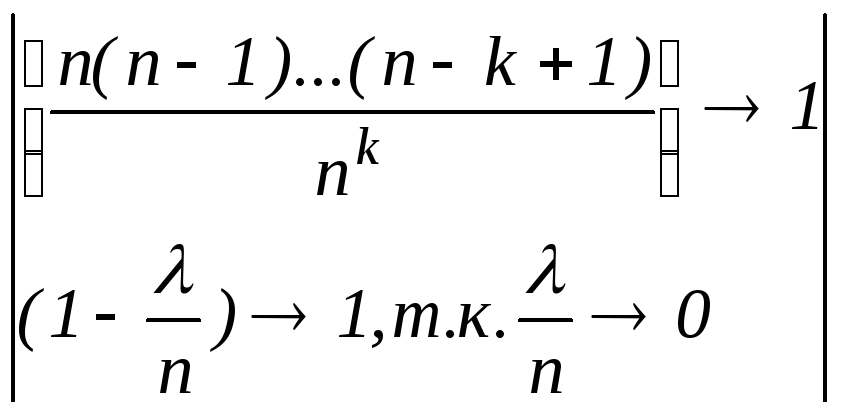
при n
Теорема показывает, что пир выполнении условий : n-велико, p-мало, -фиксированная — биномиальные вероятности хорошо аппроксимируются пуассоновскими.
Более тщательная оценка:
,
для
любых k=0,1,…,n
Интерпретация пуассоновского распределения, приходящая из биномиального, есть закон редких явлений.
Пример 1. Система коммутаций на АТС содержит n=50000 независимо работающих элементов. Вероятность отказа каждого за время Т равна p=210-5
-
Найти среднее (по распределению) число отказавших за время Т элементов и наиболее вероятное число отказавших элементов.
-
Какова вероятность, что за время Т откажет не менее 2-х элементов?
Решение.
Очевидно, что Х-(число отказавших за время Т элементов)~В(50000, p=210-5), но np= = 5104210-5=1.
1) Используем аппроксимацию:
mx=np=1 — среднее число
Наиболее вероятное
число отказавших элементов тоже равно
1 (P{X=k}=
,
P{X=k}=
k=1)
2) Используем аппроксимацию Пуассона:
P{X
2}=1-p{X<2}=1-p0-p1=1-e-1-
e-1=1-2e-1=1-0,7358=0,2642
IV. Геометрическое распределение
Определение: Говорят, что "Х распределена по геометрическому закону с параметром р>0 (Запись: Х~Гео(р)), если Ex=N, P{X=xk}=qk-1p
Это распределение встречается в опытах до 1-го успеха (включительно) по схеме Бернулли, где х-число проведенных опытов до 1-го успеха.
Нормировка:
=
=
=1