12. Общие линейные модели. Регрессионная матрица. Матрица плана. Примеры.

Общая модель линейной (относительно оцениваемых параметров ) может быть записана в виде :, i =1,2…. (1), где - случайные погрешности.

Введём замену: .

Тогда систему (1) можно записать в виде матричного уравнения: .(2)

Параметр оценивается в зависимости от предположений о природе матрицыX и распределения ошибок . Погрешностьможет быть естественной ошибкой, свойственной самому эксперименту, или может быть ошибкой в измерении параметра.

Матрица X, размера называетсярегрессионной матрицей, или матрицей регрессии.

При этом значения выбираются таким образом, чтобы столбцы этой матрицы были линейно- независимыми, т.е., чтобы ранг этой матрицы равнялсяk (число столбцов). Однако в некоторых случаях при планировании эксперимента элементы матрицы X выбираются равными только 0 или 1. Тогда столбцы матрицы X могут оказаться линейно-зависимыми. В этом случае матрица X называется матрицей плана.

Модель (1) является весьма общей.

Например, полагая , получаем так называемуюполиномиальную модель: ,i =1,2….

Модель: - является частным случаем модели (1). Существенная черта модели (1) заключается в том, что она линейна относительно параметра.

Нелинейной моделью является, например, такая модель: ,i =1,2….

13.Линейная регрессия с гауссовыми ошибками. Пример.

Пусть распределение вектора не зависит от Х и нормали, причем выборочное среднее этого вектора нулевое. Это значит, что оно представляет нулевой вектор каждая из компонент которого есть выборочное среднее для соотв. компонента вектора.

. Дисперсия компонент вектораравна. ;

Одним из методов получения оценки векторов явл. метод наименьших квадратов (МНК).

Суть в минимизации суммы по отношению к неизв. пар-ру.

Положим , тогда изполучим, что.

Указанная сумма, т. е. с одной стороны есть длина вектора.

с другой стороны .будет минимальной, когда длина вектора будет минимальной, а это значит, если(1)

Из этих ур-ний вектор определяется однозначно, если к тому же столбцы матрицы Х лин. независимы , то сущ. единственный вектортакое, чторешение (1).

Подставив последнее рав-во в (1) получаем так называемое нормальное ур-ние: (2)

Т. к. ранг матрицы Х равен k, то матрица невырожденная, а зн. ур-ние (2) имеет единственное решение.(3)

Это решение наз. оценкой наим. квадратов вектора . Остатками наз. эл-ты вектора е

Е-единич. матрица порядка п.

Минимальное значение наз. остаточной суммой квадрата, оно равно

(4)

Заметим, что ие единственные.

Пример: Пусть и-это независимые СВ со средними значениямии 2соответственно. Найти оценку наименьших пар-ров для пар-раи остаточную сумму квадрата.

Решение:

, ,,.

Находим оценку для по (3)

По (4) найдем остаточную сумму квадрата

14.Свойства оценок наименьших квадратов.

1. Если распределение -нормальное, то оценкаявляется наилучшей несмещенной оценкой для(в классе всех несмещенных оценок, т. е.и любая другая оценка’) . имеет большую чем дисперсию. Оценка, являющаяся при этом оценкой максимального правдоподобия для, эффективная оценка для.

2. Если ,,i=1,2,… и ковариация , то свойство (1) также будет иметь место и в случае, распределениене является нормальным. Действительно,==

Теорема. Пусть - оценка наименьших квадратов для, тогда в классе всех линейных оценок линейной комбинации, где- это вектор-строка, у которогоj-ый элемент равен 1, а все остальные равны 0. Оценка является единственной оценкой обладающей минимальной дисперсией.

Эта теорема остаётся в силе и тогда, когда ранг матрицы X меньше k. В общем случае МНК оценки теряют оптимальные свойства. Когда общее для всех распределение не является нормальным, оценка наименьших квадратов дляне совпадает с асимптотической эффективной оценкой максимального правдоподобия, но является асимптотически эффективной.

Ортогональные матрицы плана.

Если матрицу Х можно разбить на m совокупность столбцов так, чтобы для всехij столбцы матрицы были ортогональны столбцам матрицы, т. е. матрицу

=0, при ij , то матрицу плана наз. ортогональной.

Разобьем соотв. образом и значение .

Пусть -это ранг матрицы, причем, гдеk-ранг матрицы .

Из равенства с учетом=0, приij получаем

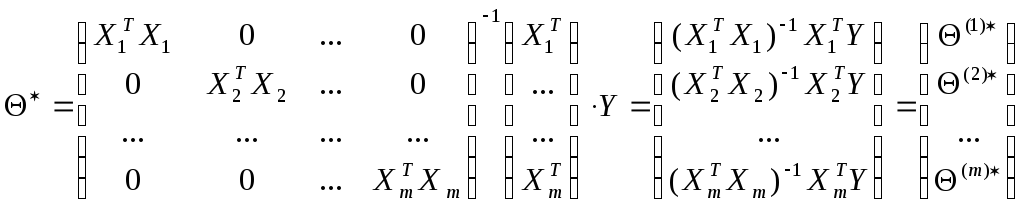
Это означает, что в случае ортогональной матрицы плана МНК (метод наименьших квадратов) оценки каждого столбца не зависимы друг от друга и не изменяются, если какие-либо из них положить =0.

Остаточная сумма квадратов в этом случае имеет вид:

.

Если про какие-то значения известно, что они =0, то величина остаточной суммы квадратов будет больше.

Т. к. эти величины независимые между собой целесообразна независимая проверка гипотез рав-ва 0 каждой из этих оценок.

Это свойство широко используется в дисперсионном анализе.

16. Проверка гипотез в линейной регрессионной модели.

Наблюдаемое значение находится по формуле

, где ,коэф-т матрицыпри

Критическое значение будет для всех одно, нах-ся по таблице Стьюдента по уровню значимости и числу степеней свободы:. Если, то теоритически коэф. регрессиипринимается равным нулю с вероятностью ошибки, т.е. выборочный коэф.оказался не значительным. В этом случаи соответствующий фактор выводится из модели.

Обычно поступают следующим образом: на каждом этапе рассчитывают эмпирические значимости всех коэф. регрессии. Эти значимости ранжируются по значениям их модулей, если тип значения меньше теоретической значимости, то данный фактор вводится из модели. Расчеты повторяются до тех пор, пока не останутся только значимые факторы (т.е. покане будет больше)

П2. доверительный интервал для коэффициентов регресии.

Значение распределений и оценок параметров регресии позволяют построить доверительные интервалы для их теоритических значений который имеет вид: