Лекции / 4

4.Числовые характеристики выборки

Эмпирическая функция распределения дает полное представление о распределении выборки генеральной совокупности. Однако на практике такая полная характеристика, как правило, не нужна. Достаточно знать некоторые особенности этого распределения, которые и дают числовые характеристики.

Опр1. Выборочным среднем наз. сумма произведений значений вариант на соотв-щие им относительные частоты =

Опр2. Выборочной дисперсией наз сумма произведений квадратов отклонений значений вариант от выборочного среднего на соот-щие относительные частоты.

Дисперсия служит для оценки рассеяния вариант около выборочного среднего.

Опр3. Выборочным среднем квадратическим отклонением наз

Опр4. Исправленной выборочной дисперсией наз величина

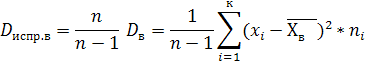
Опр5. Эмпирическим начальным моментом к-ого порядка наз выборочное среднее св

=

Опр6. Эмпирическим центральным моментом к-ого порядка наз выборочное среднее отклонение cв от выборочного среднего к-ого порядка

== =

Из опр-ий получаем:,

Опр7. Модой вариационного ряда наз варианту, имеющуюся наибольшую частоту. Обозн

Опр8. Медианой вариационного ряда наз варианту, делящуу ряд на 2 равные части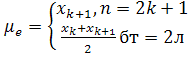

Опр9. Коэфицентом вариации наз процентное соотношение выборочного среднего квадратического отклонения к выборочному среднему

V=*100%

Коэф. вариации служит для сравнения 2 рядов по степеням рассеяния вокруг их выборочного среднего. Тот ряд имеет большее рассеяние у которого коэф. Вариации больше