Лекции / 7

Метод наибольшего правдоподобия (Фишер).

Этот метод исп. в том случае, когда известен вид ф-ии распределения. Он состоит в построении по этой ф-ии так называемой ф-ии наибольшего правдоподобия и нахождению её максимума.

Пусть СВ Х в результате n испытаний принимает знач. . Будем считать, что закон распределения СВ Х известен: для дискретной СВ в виде вероятности, а для непрерывной в виде плоскости распределения вероятности f(x), но известны параметры распределения.

О.: Ф-ей правдоподобия L(x) СВ Х наз. ф-ия - дискр. СВ.

Из опр.что ф-ия. правдоподобия явл. вероятностной мерой выборки чем вероятнее правдоподобие при фиксированном выборка , тем больше значение ф-ии правдоподобия.

О:. Оценкой наибольшего правдоподобия прарам. наз.такое значение , при котором ф-ия правдоподобия достигает своего максимума.

О:. Логарифмической ф-ей правдоподобия наз. логарифм от ф-ии правдоподобия.

Ф-ии L и logL достигают своего max при одном и том же значении приотыскании max L переходят к отысканию max log. При отыскании т. max ф-ии logL можно пользоваться схемой:

1.

2. из урав. правдоподобия: =0 нах. Критические точки ф-ии lnL.

3. находят если это выражение <>0эта т. max.

Пример: найти методом наибольшего правдоподобия по выборке .Оценку неизвестного пар-ра показательного распределения, плотн. Распределения вероятности кот-го ,x0. Восп-ся методом наиб. правдо-я. Для чего составим ф-ю правдоподобия по данной выборке.

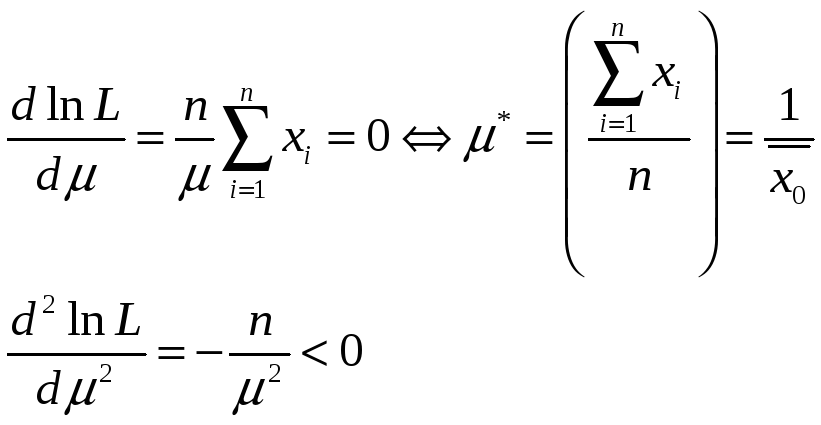
-оценка наибольшего правдоподобия для параметра .

Замечание: метод моментов отлич-ся простотой, однако оценки, получ-е этим методом смещены и мало эффективны. Исключение составляет норм-е распределения. Метод найб-го правдоподобия даёт состоят-ю оценку, если сущ. эффективная оценка, то метод наиб-го правдоподобия даёт её n оценки полученные этим методом асимптотически эффективны.