41. Знакопеременные и знакочередующиеся ряды. Теорема Лейбница о сходимости знакочередующихся рядов

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

яд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:

Теорема Лейбница формулируется следующим образом. Знакочередующийся ряд

сходится, если выполняются оба условия:

1. 

2. 

Следствие

Из теоремы Лейбница вытекает следствие, позволяющее оценить погрешность вычисления неполной суммы ряда:

Остаток сходящегося знакочередующегося ряда будет по модулю меньше первого отброшенного слагаемого:

Билет 11

11.Докозательство формулы Эйлера решением дифференциального уравнения

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями.

Формула Эйлера утверждает, что для любого действительного числа выполнено следующее равенство:

,

где —основание натурального логарифма,

 — мнимая единица.

42. абсолютная сходимость числовых рядов.

Сходящийся ряд называется сходящимся абсолютно, если сходится ряд из модулей , иначе — сходящимся условно.

Аналогично, если несобственный интеграл от функции сходится, то он называется сходящимся абсолютно или условно в зависимости от того, сходится или нет интеграл от ее модуля .

В случае общего нормированного пространства модуль в определении заменяется на норму.

Признаки абсолютной сходимости

Признак сравнения

Если при , то:

если ряд сходится, то ряд сходится абсолютно

если ряд расходится, то ряд расходится

Согласно критерию Коши, . Значит, 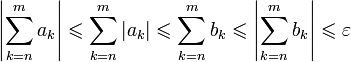, и по критерию Коши ряд сходится. Второе утверждение следует из первого, так как если бы ряд сходился, то и ряд сходился бы.

Признак сходимости рядов с монотонно убывающими членами[править | править исходный текст]

Пусть . Тогда ряд сходится тогда и только тогда, когда сходится ряд 

Билет 12

12 Однородные диф уравнения вида

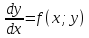
Обыкновенное уравнение первого порядка называетсяоднородным относительно x и y, если функция являетсяоднородной степени 0:

.

Однородную функцию можно представить как функцию от :

.

Используем подстановку , а затем воспользуемсяправилом произведения: . Тогда дифференциальное уравнениесводится к уравнению с разделяющимися переменными:

.

43. Знакопеременные ряды. Теорема Римана для знакопеременных рядов (формулировка)

Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.

Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.

Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов.

Определение 6. Числовой ряд вида u₁-u₂+u₃-u₄+…+     +(-1)^n-1.u_n+…, где u_n – модуль члена ряда, называется знакочередующимся числовым рядом.

Теорема.

Пусть ряд сходится условно, тогда для любого числа S можно так поменять порядок суммирования, что сумма нового ряда будет равна S.

Составим ряд из положительных элементов ряда и обозначим его , а элементы ряда обозначим . Соответственно ряд из модулей отрицательных элементов обозначим Следовательно ряд можно представить как: . Исходя из свойств условно сходящихся рядов и — расходятся, а исходя из свойств остатка ряда все остатки и — расходятся в каждом из этих рядов начиная с любого места можно набрать столько членов, чтобы их сумма превзошла любое число. Пользуясь этим произведем перестановку членов ряда : Сначала возьмем столько положительных членов ряда (не меняя их порядок), чтобы их сумма превзошла S: S За ними запишем столько отрицательных членов ряда (не меняя их порядок), чтобы общая сумма была меньше S: S Этот процесс мысленно продолжаем до бесконечности. Таким образом все члены ряда встретятся в новом ряду. Если всякий раз, выписывая члены и , набирать их не больше, чем требуется для неравенства, то разница между частичной суммой нового ряда и S по модулю не превзойдет последнего написаного члена. Поскольку из свойств условно сходящихся рядов: и , то новый ряд сходится к S. ■

Билет 13

13.Линейные диф уравнения вида 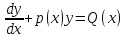.Решение способом подстановки.

Линейным дифференциальным уравнением 1-го порядка называется уравнение вида: или . Методы решения:

Метод вариации произвольных постоянных:

Приравнять правую часть к нулю: и решить уравнение с разделяющимися переменными.

Подставить вместо С некую функцию от x и найти решение уравнения.

Применение подстановки y = uv, где u и v - функции от x, 1) получим уравнение: [u' + p (x) u] v + v' u = q (x). 2) Приравнять выражение в квадратных скобках к нулю и найти u (x). 3) Из [u' + p (x) u] v + v' u = q (x) найти v. 4) Из y = uv найти y.

Способ подстановки.

Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.  Дифференциальное уравнение вида

преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:

44. Бином Ньютона формулировка

Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид

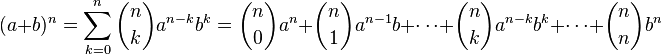
где 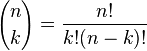—биномиальные коэффициенты, — неотрицательноецелое число.

В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное действительное (или дажекомплексное) число. В этом случае бином представляет собой бесконечный ряд (см. ниже).

Доказать формулу бинома Ньютона  , где(число сочетаний изn элементов по m), , причем полагают 0! = 1.

Решение.

При n = 1 имеем

Остается показать, что из предположения справедливости утверждения для n следует, что

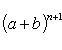
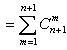
В самом деле,

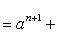
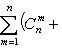
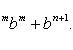
Используя соотношения

окончательно имеем

Билет 14

14. Линейные диф уравнения .Метод Лагранжа.

Линейным дифференциальным уравнением 1-го порядка называется уравнение вида: или . Методы решения:

Метод вариации произвольных постоянных:

Приравнять правую часть к нулю: и решить уравнение с разделяющимися переменными.

Подставить вместо С некую функцию от x и найти решение уравнения.

Применение подстановки y = uv, где u и v - функции от x, 1) получим уравнение: [u' + p (x) u] v + v' u = q (x). 2) Приравнять выражение в квадратных скобках к нулю и найти u (x). 3) Из [u' + p (x) u] v + v' u = q (x) найти v. 4) Из y = uv найти y.

Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения

Метод состоит в замене произвольных постоянных в общем решении

соответствующего однородного уравнения

на вспомогательные функции , производные которых удовлетворяют линейной алгебраической системе

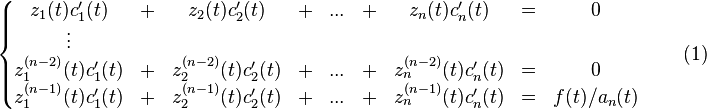
Определителем системы (1) служит вронскиан функций , что обеспечивает её однозначную разрешимость относительно .

Если  — первообразные для , взятые при фиксированных значениях постоянных интегрирования, то функция

является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам.

Метод вариации произвольных постоянных для построения решений системы линейных дифференциальных уравнений в векторной нормальной форме

состоит в построении общего решения (1) в виде

где  — базис решений соответствующего однородного уравнения, записанный в виде матрицы, а векторная функция , заменившая вектор произвольных постоянных, определена соотношением . Искомое частное решение (с нулевыми начальными значениями при имеет вид

Для системы с постоянными коэффициентами последнее выражение упрощается:

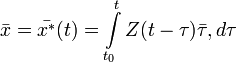
Матрица называется матрицей Коши оператора .

45. Функциональный ряд. Понятие области сходимости.

Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция .

—n-ная частичная сумма.

Сходимость

Ряд называется сходящимся поточечно, если последовательность его частичных сумм сходится поточечно.

Ряд называется сходящимся равномерно, если последовательность его частичных сумм сходится равномерно.

Прошу любить и жаловать степенной ряд .

Переменная  может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»: Если , то  Если , то  Если , то  Если , то 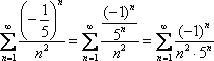 И так далее.

Очевидно, что, подставляя в  то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд  будет сходиться. Такое множество и называется областью сходимости ряда.

Билет 15

15. уравнение Бернулли

равнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде

где a(x) и b(x) − непрерывные функции.  Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когдаm = 1, уравнение преобразуется в уравнение с разделяющимися переменными.  В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки

Новое дифференциальное уравнение для функции z(x) имеет вид

и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка. 

46. Степенной ряд. Теорема Абеля.

Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:

в котором коэффициенты берутся из некоторогокольца .

Утверждение

Пусть — степенной ряд с комплексными коэффициентами и радиусом сходимости .

Если ряд является сходящимся, тогда:

.

Доказательство

Заменой переменных , можно считать . Также (необходимым подбором ) можно предположить . Обозначим частичные суммы ряда . Согласно предположению и нужно доказать, что .

Рассмотрим . Тогда (приняв ):

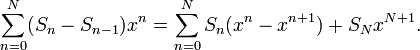
Отсюда получается .

Для произвольного существует натуральное число , что для всех , поэтому:

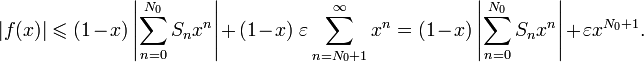
Правая часть стремится к когда стремится к 1, в частности она меньше при следовании к 1.

Билет 16

16. особые решения диф уравнений

Решение дифференциального уравнения

(1)

называется особым, если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точкету же касательную, что и решение, но не совпадающее с ним в сколь угодно малой окрестности. График особого решения будем называть особой интегральной кривой уравнения (1). Если функцияи ее частные производныеинепрерывны по всем аргументам, то любое особое решение уравнения (1) удовлетворяет также уравнению

(2)

Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).

Полученное после исключения из (1) и (2) уравнение

(3)

называется p-дискриминантом уравнения (1), а кривая, определяемая уравнением (3), называется p-дискриминантной кривой (коротко ).

Часто бывает так, что распадается на несколько ветвей. Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.

47. Радиус и интервал сходимости степенного ряда.

Радиус и интервал сходимости степенного ряда

В соответствии с теремой Абеля отметим: при условии, чтоявляется точкой сходимости ряда (30.2) ряд предполагает сходимость абсолютно во всех точках интервалаЕслиесть точка расходимости (30.2), то во всех точках интерваловряд расходится. Тогда заключим: имеется такое число, что наряд (30.2) сходится абсолютно, а нарасходится. В этом случае справедлива нижеобозначенная теорема.

Т: Область сходимости ряда (30.2) — это интервалпредполагается расходимость ряда.

Интервалопределен в качестве его радиуса сходимости. Существуют некоторые ряды, для которых интервал сходимости вырождается в точку, при этом, имеются и такие ряды, для которых интервал охватывает всю ось. Если, то ряд может расходиться и сходиться. Это зависит от конкретного ряда.

Запишем способ нахождения радиуса сходимости ряда (30.2). Исследуем ряд, составленный их абсолютных величин его членов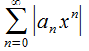и используем по отношению к нему признак Даламбера:

 

 

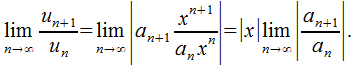
При условии, что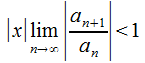(иначе выражаясь,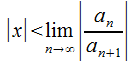) ряд из абсолютных величин членов (30.2) сходится и ряд (30.2) сходится абсолютно. Запишем

 

(30.4)

 

Если, то ряд (30.2) расходится, поскольку общий член рядане стремится кПолучается, что формула (30.4) обеспечивает радиус сходимости.

Пример: Определить радиус и интервал сходимости ряда

 

 

 

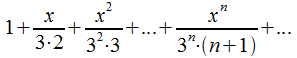
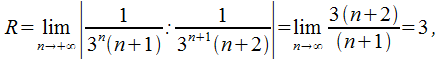
интервал абсолютной сходимостиНа концах интеграла: если, то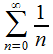представляет собой гармонический расходящийся ряд, в случае же когда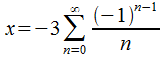— это знакочередующийся ряд, который предполагает условную сходимость. Промежутокесть область сходимости обозначенного ряда.

Ряд (30.1) можно свести к ряду (30.2) посредством осуществления замены переменной

Если ряд, то ряд (30.1) сходится абсолютно для, иначе выражаясь, сходимость имеется на интервале