Билет 1

1.Сложение и вычитание, умножение и деление комплексных чисел в алгебраической, тригонометрической и показательных формах.

Алгебраическая форма

Запись комплексного числа в виде, гдеи, называетсяалгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что ):

Тригонометрическая форма

Если вещественную и мнимуючасти комплексного числа выразить через модульи аргумент,), то всякое комплексное число, кроме нуля, можно записать втригонометрической форме

Показательная форма

Применяя формулу Эйлерак тригонометрической форме, получим показательную форму комплексного числа:

где — расширениеэкспонентыдля случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

Действия над комплексными числами.

Сравнение

 означает, что и(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

Сложение

Вычитание

Умножение

Деление

В частности,

32.Преобразование Лапласа при дифференцировании изображения. L {t sin ῳt}

t sin ῳt = (над ровно точки)

Дифференцирование изображения сводится к умножению на (-t) оригинала

или вообще

.

Билет 2

2. Первый и второй замечательный предел. Вторая модификация второго замечательного предела.

Первый замечательный предел

Доказательство

Рассмотрим односторонние пределы и и докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности ().

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке . Точка H — проекция точки K на ось OX.

Очевидно, что:

 (1)

(где  — площадь сектора )

(из : )

Подставляя в (1), получим:

Так как при :

Умножаем на :

Перейдём к пределу:

Найдём левый односторонний предел:

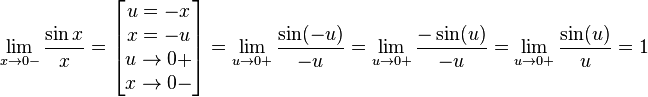
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

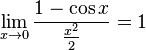
Второй замечательный предел

 или 

Модификации второго замечательного предела

, 

могут быть обоснованы.

Заметим, что второй замечательный предел раскрывает неопределенность вида , т.е. для степенно показательной функции   может быть применен, если основание  и показатель  при  (одновременно).

33. Преобразование Лапласа при дифференцировании изображения. L {t cos ῳt}

t coc ῳt = (над ровно точки)

Дифференцирование изображения сводится к умножению на (-t) оригинала

или вообще

.

Билет 3

3. Понятие производной . Её геометрический и физический смысл.

Определение: Производной функции f(x) (f'(x₀)) в точке x₀  называется число, к которому стремится разностное отношение , стремящемся к нулю.

Производные элементарных функций.

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции  y=f(x) в этой точке

Уравнение касательной к графику функции y=f(x) в точке x₀ :

Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону  x(t), то мгновенная скорость точки:

34. сумма бесконечного числа членов убывающей геометрической прогрессии

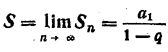
Итак, сумма бесконечно убывающей геометрической прогрессии равна первому члену этой прогрести, деленному на единицу минус знаменатель этой прогрессии

Билет 4

4. правила дифференцирования

35. Необходимый признак сходимости числового ряда

Теорема (необходимый признак сходимости числового ряда). Если ряд (1) сходится, то его общий член стремится к нулю, то есть . Если не выполняется, то расходится. Достаточное условие расходимости ряда: если предел или этот предел не существует, то ряд расходится. Необходимый признак сходимости ряда недостаточен для сходимости, поскольку существуют ряды, которые расходятся, но необходимый признак сходимости для них выполняется. 

Билет 5

5. метод неопределенных коэффициентов.

Разложение знаменателя на множители.

Разложение дроби в виде суммы простейших дробей с неопределенными коэффициентами.

Группировка числителя с одинаковыми степенями x.

Получение системы линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных.

Решение СЛАУ: методом Крамера, методом Гаусса, методом обратной матрицы или методом исключения неизвестных.

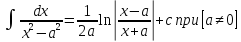
36. признаки сравнения числовых рядов

Необходимый признак сходимости, вообще говоря, не гарантирует сходимости ряда. Сходимость или расходимость ряда устанавливается с помощьюдостаточных признаков. Признаки сравнения, которые мы рассмотрим ниже, как раз и представляют собой достаточные признаки сходимости или расходимости рядов.

Признаки сравнения рядов

Даны два ряда и− такие, чтодля всехn. Тогда справедливы следующие признаки:

 Если сходится, тотакже сходится;

 Если расходится, тотакже расходится.

Предельные признаки сравнения рядов

Пусть даны два ряда и, у которых членыa_n и b_n положительны для всех n. Тогда справедливы следующие предельные признаки:

Если 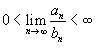, то оба рядаилибо сходятся, либо расходятся;

Если , то рядсходится, если сходится ряд;

Если 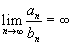, то рядрасходится, если расходится ряд.

Так называемый обобщенный гармонический ряд сходится приp > 1 и расходится при 0 < p ≤ 1. 

Билет 6.

6. Интегрирование по частям

1. Интегри́рование по частя́м — один из способовнахожденияинтеграла. Суть метода в следующем: если подынтегральнаяфункцияможет быть представлена в виде произведения двухнепрерывныхигладкихфункций (каждая из которых может быть какэлементарнойфункцией, так икомпозицией), то справедливы следующие формулы

для неопределённого интеграла:

или

для определённого:

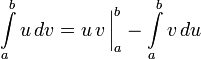
Предполагается, что нахождение интеграла проще, чем. В противном случае применение метода неоправданно.

2.

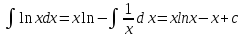
37. Признак Д”Аламбера Сходимости числовых рядов.

При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.

Если для числового ряда

существует такое число , , что начиная с некоторого номера выполняется неравенство

то данный ряд абсолютно сходится; если же, начиная с некоторого номера

то ряд расходится.

Признак сходимости д’Аламбера в предельной форме

Если существует предел

то рассматриваемый ряд абсолютно сходится если , а если  — расходится.

Замечание. 

Если , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.

Доказательство

, тогда существует , существует , для любого . Ряд из сходится (как геометрическая прогрессия). Значит, ряд из сходится (по признаку сравнения).

, тогда существует . для любого . Тогда не стремится к нулю и ряд расходится.

Билет 7

7. Универсальная тригонометрическая подстановка.

Универсальная тригонометрическая подстановка, в англоязычной литературе называемая в честь Карла Вейерштрасса подстановкой Вейерштрасса, применяется винтегрировании для нахожденияпервообразных, определённых и неопределённых интегралов от рациональных функций от тригонометрических функций. Без потери общности можно считать в данном случае такие функции рациональными функциями от синуса и косинуса. Подстановка использует тангенс половинного угла.

Подстановка

Рассмотрим задачу нахождения первообразной рациональной функции от синуса и косинуса. Заменим sin x, cos x и дифференциал dx рациональными функциями от переменной t, и их произведением дифференциал dt, следующим образом:^[1]

для значений x, лежащих в интервале

Введение обозначений[править | править исходный текст]

Примем, что переменная t равна тангенсу половинного угла:

В интервале −π < x < π, это даёт

и после дифференцирования получаем

Формула тангенса половинного угла даёт для синуса

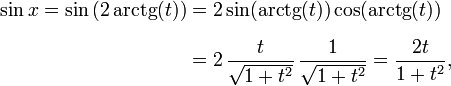
и для косинуса формула даёт

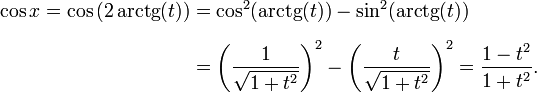
38. Радикальный признак Каши. Сходимости числового рядов.

Радикальный признак Коши — признак сходимости числового ряда:

Если для числового ряда с неотрицательными членами существует такое число ,, что, начиная с некоторого номера, выполняется неравенство, то данный ряд сходится.

Предельная форма

Условие радикального признака равносильно следующему:

То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:

Если для ряда , то если ряд сходится, если ряд расходится, если вопрос о сходимости ряда остается открытым.

Доказательство

1. Пусть . Очевидно, что существует такое , что . Поскольку существует предел , то подставив в определение предела выбранное получим:

Раскрыв модуль, получаем:

Поскольку , то ряд сходится. Следовательно, по признаку сравнения ряд тоже сходится.

2. Пусть . Очевидно, что существует такое , что . Поскольку существует предел , то подставив в определение предела выбранное получим:

Раскрыв модуль, получаем:

Поскольку , то ряд расходится. Следовательно, по признаку сравнения ряд тоже расходится.

Билет 8.

8. Гамма функция и её связь с факториалом

Гамма-функция — математическая функция, которая расширяет понятие факториала на поле комплексных чисел. Обычно обозначается .

Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязанаЛежандру.

Интегральное определение

Если вещественная часть комплексного числа положительна, то Гамма-функция определяется через интеграл

На всю комплексную плоскость функция аналитически продолжается через тождество

Существует непосредственное аналитическое продолжение исходной формулы на всю комплексную плоскость, называемое интегралом Римана-Ханкеля

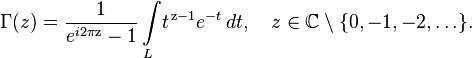
где контур - любой контур на комплексной плоскости, обходящий точку против часовой стрелки, и концы которого уходят на бесконечность вдоль положительной вещественной оси.

Последующие выражения служат альтернативными определениями Гамма-функции.

Определение по

Оно верно для всех комплексных , за исключением 0 и отрицательных целых чисел

Определение по Эйлеру]

Определение по Вейерштрассу

где — постоянная Эйлера — Маскерони.

Замечания

Интеграл выше сходится абсолютно, если вещественная часть комплексного числа положительна.

Применяя интегрирование по частям, можно показать, что тождество

выполняется для подынтегрального выражения.

А поскольку , для всех натуральных чисел 

 является мероморфной на комплексной плоскости и имеющей полюса в точках 

Связанные определенияИногда используется альтернативная запись, так называемая пи-функция, зависящая от гамма-функции следующим образом:

.

В интеграле выше, определяющем гамма-функцию, пределы интегрирования фиксированы. Рассматривают также неполную гамма-функцию, определяемую аналогичным интегралом с переменным верхним либо нижним пределом интегрирования. Различают верхнюю неполную гамма-функцию, часто обозначаемую как гамма-функцию от двух аргументов:

и нижнюю неполную гамма-функцию, аналогично обозначаемую строчной буквой «гамма»:

.

39. Интегральный признак Коши сходимости числовых рядов