3. Анализ и подсчет фактических напряжений

3.1 Определение напряжений в сечениях крыла

Критерием работоспособности конструкции (крыла, фюзеляжа или др.), т.е. близости ее к состоянию разрушения или необратимых деформаций, является величина напряжений, возникающих в силовых элементах конструкции от действия на неё эксплуатационных нагрузок: изгибающего, крутящего моментов и поперечной силы.

Сечение крыла необходимо схематизировать в соответствии с реальным расположением силовых элементов: силовой частью сечения крыла является межлонжеронная часть, длина и высота которой ра вны:

, м (3.1)

, м (3.2)

где - длина межлонжеронной части;

- высота межлонжеронной части;

- текущая хорда крыла;

- относительная толщина крыла.

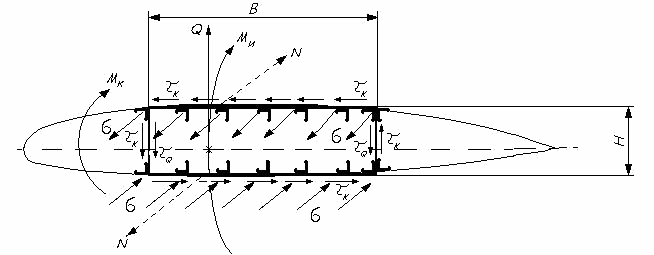
Рис.2.7. Напряжения в силовых элементах сечения крыла, возникающие от внешних сил Q, Ми

Мк.

Крыло является тонкостенной замкнутой конструкцией, основные силовые элементы которой сосредоточены в верхней и нижней панелях (обшивка, стрингеры, полки лонжеронов). При изгибе, например, вверх (от аэродинамических сил) верхняя панель сжимается, нижняя растягивается, то есть обе работают на нормальные напряжения; при этом изгибающий момент трансформируется в пару сил , напряжения от которых будут:

, Па (3.3)

, Па (3.4)

где - площадь верхней панели крыла;

- площадь нижней панели крыла.

Площадь панели определяется площадью обшивки, площадями всех стрингеров и полок лонжеронов (переднего и заднего). Т.е.:

, м² (3.5)

, м² (3.6)

где ,- толщина обшивки верхней и нижней панелей соответственно;

, - число стрингеров верхней и нижней панелей соответственно;

- площади стрингеров верхней и нижней панелей соответственно;

,,,- площади полок переднего верхнего, заднего верхнего, переднего нижнего и заднего нижнего лонжеронов соответственно.

Максимальный изгибающий момент, равный Нм, действует в корневом сечении, т.е. м. Найдем ипо формулам (3.1) и (3.2):

(м), (3.7)

(м). (3.8)

Найдем площади верхней и нижней панелей крыла по формулам (3.5) и (3.6):

(3.9)

(3.10)

Теперь мы можем найти нормальные напряжения, действующие в корневом сечении:

МПа (3.11)

МПа (3.12)

Крутящий момент в тонкостенном однозамкнутом контуре создает касательные напряжения, обратно пропорциональные толщине стенок контура:

Па (3.13)

Па (3.14)

где- площадь, охватываемая контуром, равная;

- толщина обшивки (верхней или нижней) или стенки лонжерона;

- максимальный крутящий момент, равный =13563,9 Нм;

Помимо крутящего момента на стенки лонжеронов действует поперечная сила, равная в этом сечении Н, которая создает также касательные напряжения:

МПа (3.15)

МПа (3.16)

где: - величина максимальной поперечной силы;

и - толщина стенки лонжерона (переднего или заднего).

Тогда: 1) общее напряжения от действия крутящего момента и поперечной силы на стенке переднего лонжерона равно:

МПа (3.17)

2) общие напряжения от действия крутящего момента и поперечной силы на стенке заднего лонжерона равно:

МПа (3.18)

Полученные нами напряжения снесем в таблицу:

Таблица 4

Значения напряжений в наиболее нагруженных точках крыла

Напряжение
Значение, МПа	49	58	2,7	1,03	0,26	0,3	3,02	0,75

МПа, МПа.

Полученные напряжения сравниваем с теми напряжениями, при которых конструкция ещё не испытывает остаточных деформаций, т.е. с напряжениями пропорциональности или. Для дюралевых сплавов, из которых изготовлено большинство силовых элементов современных самолетов эти значения равны: (см. под Таблицей 4).

Сравнив данные таблицы 4 с пределами пропорциональности, можно сделать вывод о том, что при попадании самолета в резкий вертикальный порыв со скоростью ветра W=15 м/с, крыло самолета Як-40 не разрушится и не приобретет остаточных деформаций, т.к. напряжения, действующие на крыло, меньше пределов пропорциональности.