
Ris_DSP / TZOS_red4_ch1_for_Tablet
.pdf
61
Вещественная часть ReF(k) комплексного ДПФ имеет четную симметрию относительно N/2, а мнимая часть ImF(k) имеет нечетную симметрию относительно N/2.
Таким образом, на основе вещественных компонентов ДПФ могут быть сгенерированы отрицательные частотные компоненты комплексного ДПФ.
рис.3 Комплексное ДПФ. а) входные отсчеты х(п), б) вещественная часть ДПФ, в) мнимая часть ДПФ,
г) модуль вещественного ДПФ
2.3.7 СПОСОБЫ УСРЕДНЕНИЯ ОЦЕНОК СПЕКТРА
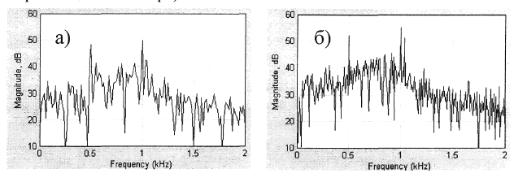
При использовании классических методов оценка спектральной плотности мощности случайного процесса вычисляется по N отсчетам, взятым непосредственно из сигнала. С ростом числа используемых отсчетов значения спектра начинают все быстрее флуктуировать. На рис. 1 приведены оценки спектра (для N=256 и N=512) «тестового» сигнала представляющего собой сумму трех гармоник 500Гц, 1000Гц, 1040Гц и шума. Видно, что с увеличением N спектр становится все более изрезанным (увеличивается дисперсия оценки спектра).
62
рис.1. Оценки спектра трех гармоник с шумом а) число отсчетов N=256, б)
число отсчетов N=512.
Для уменьшения изрезанности спектра необходимо применить какоелибо усреднение. Бартлетт (Bartlett) предложил разделить N выборок анализируемого сигнала x(n) на M N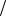 L неперекрывающихся сегментов длиной L каждый, вычислить для каждого сегмента спектр
L неперекрывающихся сегментов длиной L каждый, вычислить для каждого сегмента спектр
L 1 |
j |
2 |
|
nk |
||||
Fi(k) xi (n)e |
|
|
|
|||||
|
L , k 0,L 1 , |
|||||||
n 0 |
|
|
|
|
|
|||
и затем эти спектры усреднить |
|
|
|
|
|
|||
|
|
|
1 |
|
|
M |
||
|
|
|
|
Fi(k). |
||||
|
F(k) |
|||||||
|
|
|
||||||
|
|
|
|
M i 1 |
||||
Этот метод получил название - периодограммный. |
||||||||
На рис.2 «тестовый» сигнал разбит на четыре неперектрывающиеся сегмента по 512 отсчетов (рис.2а). Для каждого i-го сегмента вычисляются частные спектры (рис.2б). Усредненный по четырем временным сегментам спектр приведен на рис.4а.
|
Уэлч (Welch) внес в метод Бартлетта два усовершенствования: |
|||
использование |
весовой функции (окна) (n) и разбиение сигнала на |
|||
M |
|
N |
перекрывающихся на величину Lсегментов. |
|
L L 1 |
|
|||
Для каждого i-го сегмента вычисляются частные спектры
L 1 |
j |
2 |
nk |
Fi(k) xi (n) (n)e |
|
||
|
L , k 0,L 1 , |
||
n 0
которые затем также усредняются
63
1 M
F(k) M i 1 Fi(k).
Применение окна позволяет ослабить растекание спектра (просачивание) ценой ухудшения разрешающей способности. Перекрытие сегментов введено для того, чтобы увеличить их число и уменьшить дисперсию оценки спектра. Этот метод получил название -
модифицированный периодограммный.
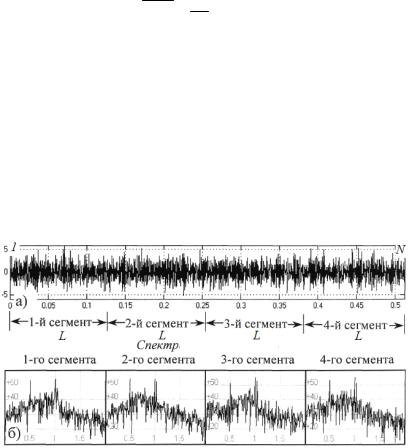
На рис.3 «тестовый» сигнал разбит на 7 перектрывающихся сегментов (рис.3а). В каждом сегменте 512 отсчётов, перекрытие сегментов 50% (256 отсчетов). Для каждого взвешенного окном Ханна сегмента вычисляется спектральная плотность (рис.3б). Усредненный по перектрывающимся сегментам спектр приведен на рис.4б.
рис.2. Оценка спектра методом Бартлетта, а) разбивка входного процесса на сегменты, б) оценки спектра сегментов
64
рис.3. Оценка спектра методом Уэлча, а) разбивка входного процесса на сегменты, б) оценки спектра сегментов взвешенных окном Ханна
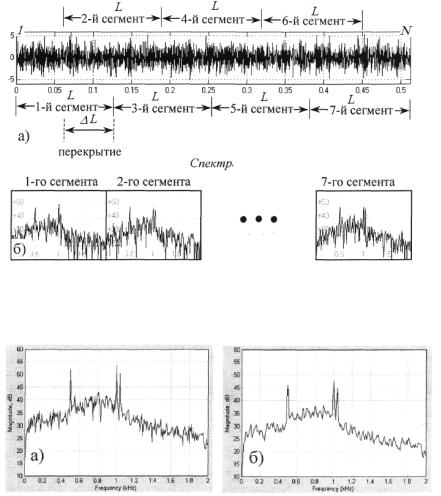
рис.4. Усредненная оценка спектра (N=512) а) по методу Бартлетта, б) по методу Уэлча
При выборе функции окна и параметров усреднения спектра (количество сегментов и величина их перекрытия) необходимо принимать компромиссное решение между снижением уровня боковых лепестков спектра, дисперсией оценки спектра и приемлемым спектральным разрешением.
65
2.4.ЦИФРОВЫЕ СОГЛАСОВАННЫЕ ФИЛЬТРЫ
Ксигналам, используемым в радио - и гидролокации, предъявляются противоречивые требования. С одной стороны желательно иметь сигналы малой длительности, чтобы, например:
снизить влияние реверберационных помех;
повысить точность измерения дистанции до объекта локации и разрешающую способность по дальности,
с другой стороны – большой длительности, чтобы:
снизить влияние широкополосных шумовых помех;
увеличить дальность обнаружения объектов;
повысить точность измерения скорости движения объекта локации;
повысить точность измерения угловых координат объекта локации. Для разрешения этих противоречий наряду с простыми используются
сложные сигналы. К простым сигналам относятся сигналы с гармоническим заполнением и различной формой огибающей. Огибающая может быть: прямоугольной, колокольной, в форме трапеции, экспоненциальной, треугольной и т.д.
Для простых сигналов с прямоугольной огибающей:
Sпр(t) A(t) cos( ct ), t (0,Tc) , где
A(t) – огибающая сигнала; fc= с/2 – несущая частота; - начальная фаза, существует однозначная связь между длительностью сигнала и его полосой: fc=1/Тс. То есть для простых сигналов база сигнала = fc Тс 1.
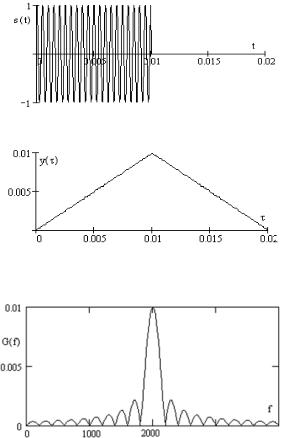
Спектральные и корреляционные характеристики простого сигнала представлены на рисунках: рис.2.56 - простой сигнал с прямоугольной огибающей (Тс=10мс, fc=2кГц, =1); рис.2.57 – модуль АКФ простого сигнала; рис.2.58 – спектральная плотность простого сигнала.
Для сложных сигналов нет однозначной связи между длительностью сигнала и шириной его спектра. Для них база = fc Тс 1, т.к. ширина спектра сложных сигналов определяется не столько длительностью сигнала, сколько характеристиками внутриимпульсной модулирующей функции. Сложные сигналы подразделяются на:
фазомодулированные - ФМ (фаза сигнала внутри импульса меняется по заданному закону);
с частотной модуляцией - ЧМ (частота сигнала внутри импульса меняется по заданному закону);
66
случайные (по случайному закону внутри импульса меняется частота, фаза или амплитуда).
Рис.2.56. Простой сигнал
Рис.2.57. Модуль автокорреляционной функции простого сигнала
Рис.2.58. Спектральная плотность простого сигнала
ФМ сигнал – это последовательность радиоимпульсов, начальные фазы которых меняются по заданному закону. ФМ сигналы подразделяются на бинарные (фаза может принимать только два значения: 0 или ; такие сигналы часто называют - фазоманипулированные) и многофазные. Законы изменения фазы у бинарных сигналов оптимизированы в основном по двум параметрам: максимально возможная сложность сигнала (количество позиций М кода внутри импульса) и минимум бокового поля автокорреляционной функции (АКФ) ФМ сигнала. В основном используются законы Баркера (максимально – 13-позиционные; имеют
67
уровень бокового поля АКФ - =1/M) и М-последовательности (количество позиций кода внутри импульса М=2к-1, где к – целое число;
уровень бокового поля АКФ - 1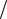

 M ). Для бинарных ФМ сигналов:
M ). Для бинарных ФМ сигналов:
M
S(t) A(t) Em(t) cos( ct m(t) ), t (0,Tc), где
m 1
M – число позиций кода (число дискрет) внутри импульса; m –номер дискреты; д Tc 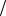 M - длительность дискреты ФМ сигнала;
M - длительность дискреты ФМ сигнала;
|
|
1 |
при д (m 1) t д m |
Em(t) |
- огибающая дискреты; |
||
|
|
0 |
придругих t |
|
m |
(t) 0 |
- начальная фаза несущей частоты внутри дискреты. |
|
|
|
|
|
|
|
|
Ширина спектра ФМ сигнала fс=1/ д.
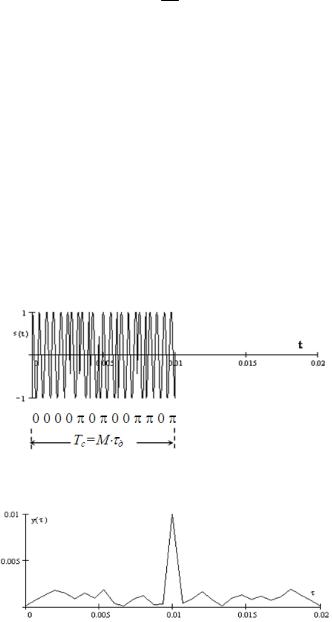
Спектральные и корреляционные характеристики ФМ сигнала представлены на рисунках: рис.2.59 - ФМ сигнал (Тс=10мс, fc=2кГц, М=15,=15); рис.2.60 – модуль АКФ ФМ сигнала; рис.2.61 – спектральная плотность ФМ сигнала.
Рис.2.59. ФМ сигнал, кодированный по закону M-последовательности
(М=15)
Рис.2.60. Модуль автокорреляционной функции ФМ сигнала

68
Рис.2.61. Спектральная плотность ФМ сигнала
К ЧМ сигналам относятся, например, сигналы с линейной частотной модуляцией (ЛЧМ), с дискретной частотной модуляцией (ДЧМ), с гиперболической частотной модуляцией (ГЧМ).
Для ЛЧМ сигналов:
S(t) A(t) cos( |
t |
at2 |
), t (0,T ), где |
|
|||
c |
2 |
c |
|
|
|
||
a [рад/с2]= коэффициент девиации частоты (девиация частоты внутри импульса может быть убывающей или возрастающей); fc= с/2 - начальная частота сигнала. Ширина спектра ЛЧМ сигнала с=a Tc.
Спектральные и корреляционные характеристики ЛЧМ сигнала представлены на рисунках: рис.2.62 - ЛЧМ сигнал (Тс=10мс, fc=2кГц, а=942 103 рад/с2, =15); рис.2.63 – модуль АКФ ЛЧМ сигнала; рис.2.64 – спектральная плотность ЛЧМ сигнала.
Рис.2.62. ЛЧМ сигнал
69
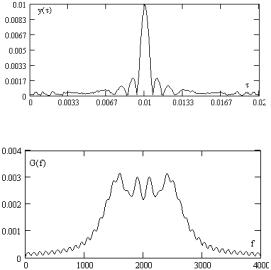
Рис.2.63. Модуль автокорреляционной функции ЛМЧ сигнала
Рис.2.64. Спектральная плотность ЛЧМ сигнала
Универсальной характеристикой, описывающей свойства сигналов, является функции неопределенности (ФН). Она является мерой сходства между комплексной огибающей сигнала S(t) и её копией, сдвинутой по времени на и по частоте - на f.
|
|
H( f , ) |
S(t ) S*(t) ej2 ftdt. |
|
|
Функции неопределенности простого, ФМ и ЛЧМ сигналов представлены на рис.2.65, 2.66, 2.67, соответственно.
Сечение ФН плоскостью, перпендикулярной плоскости ( f, ) и проходящей через f=0, соответствует АКФ сигнала (рис.2.57, 2.60, 2.63) и характеризует разрешающую способность сигнала по задержке (т.е. разрешающую способность по дистанции и точность измерения дистанции до объекта).
Сечение ФН плоскостью, перпендикулярной плоскости ( f, ) и проходящей через =0, характеризует разрешающую способность сигнала по частоте f (т.е. точность измерения доплеровского сдвига частоты эхосигнала).
70
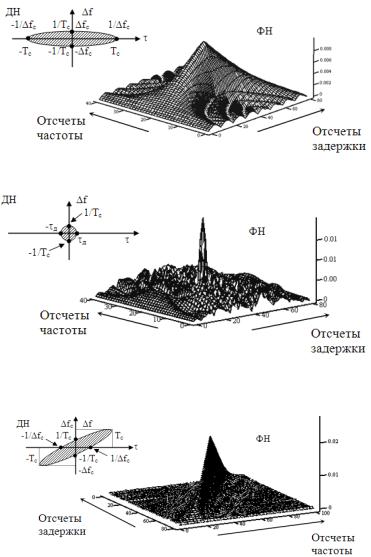
Рис.2.65. Функция и диаграмма неопределенности простого сигнала
Рис.2.66. Функция и диаграмма неопределенности ФМ сигнала
Рис.2.67. Функция и диаграмма неопределенности ЛЧМ сигнала
При анализе свойств сигналов часто используют диаграмму неопределенности (ДН) (рис.2.65, 2.66, 2.67) - проекцию сечения ФН на плоскость ( f, ).
Анализ представленных ДН показывает:
