
Ris_DSP / TZOS_red4_ch1_for_Tablet
.pdf
51
площадь под кривой Gxx(k) также характеризует среднюю мощность процесса x(n). Т.е. Gxx(k) представляет собой функцию плотности (мощности на единицу частоты), которая показывает распределение мощности случайного процесса x(n) по частоте.
Для ограниченного объема |
данных |
(m 0,N 1) |
определятся |
|||||||||||
соответственно: |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
автоспектр |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
N 1 |
|
|
j |
|
mk |
|
|
|
|
|
||
|
|
Gxx(k) rxx(m) e |
|
N |
|
|
|
(2.27) |
|
|||||
|
|
m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
взаиный спектр |
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
N 1 |
|
|
j |
mk |
|
|
|
|
|
|||
|
|
Gxy (k) rxy (m) e |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
N . |
(2.28) |
|
||||||||
|
|
m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3.4. БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ |
|
|||||||||||
Дискретное преобразование |
Фурье |
последовательности |
x(n), где |
|||||||||||
n |
|
|
|
|
|
|
|
|||||||
0,N 1 определяется соотношением: |
|
|
|
|
|
|||||||||
|
|
N 1 |
j |
2 |
nk |
|
|
|
|
|
|
|
|
|
|
|
F(k) x(n) e |
N |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
, |
где |
k 0,N 1. |
|
|||||||
|
|
|
|
|
|
|
||||||||
n 0
Для вычисления F(k) на каждой дискретной частоте требуется N комплексных умножений и N комплексных сложений. А для получения всех N составляющих частот требуется N2 комплексных умножений и сложений. Если, например, длина массива данных N=1000, то требуется 106 комплексных операций. В этом случае использовать алгоритм дискретного спектрального анализа в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств. Эффективный способ вычисления дискретного преобразования Фурье, позволяющий существенно сократить число выполняемых операций, был предложен в 1965 г. Кули и Тьюки. Этот способ получил название - быстрое преобразование Фурье (БПФ) по основанию 2. Т.е. массив входных данных должен быть степенью 2: N=2m (32, 64, 128, 256, 512, 1024 и т.д.).
Идея БПФ состоит в разбиении исходной последовательности x(n) на две более короткие, ДПФ которых могут быть скомбинированы так, чтобы

52
получить ДПФ исходной последовательности. Например, если N является степенью двойки, то разбиения N на две N/2-точечные последовательности
число операций ДПФ |
уменьшится примерно вдвое |
(Например, |
при N=8 |
|||||||
ДПФ требует операций N2=64. После разбиения N на две |
||||||||||
последовательности |
N1=4 и |
N2=4, |
число |
операций |
ДПФ |
равно |
||||
N12 N22 32). Эту процедуру |
можно |
повторить |
над |
N/2-точечной |
||||||
последовательностью, т.е. получить N/4, N/8 и |
т.д. |
- |
точечные |
|||||||
последовательности. |
|
|
|
|
|
|
|
|
|
|
Проиллюстрируем это, переписав выражение для ДПФ в виде: |
|
|
||||||||
N 1 |
|
|
|
j |
2 |
|
|
|
|
|
F(k) x(n) WN nk , |
где |
WN e N |
. (2.25) |
|
|
|||||
n 0 |
|
|
|
|
|
|
|
|
|
|
Поворачивающий множитель WN nk периодичен с периодом N: |
|
|||||||||
WN (n mN)(k lN) WN nk |
(2.26) |
|
|
|
||||||
Если разбить N-точечную последовательность |
x(n) |
на две |
N/2- |
|||||||
точечные последовательности x1(n) и x2(n), где x1(n)=x(2n), (n 0,N /2 1)
- содержит четные члены, а x2(n)=x(2n+1), (n 0,N /2 1) - содержит нечетные члены последовательности x(n), то ДПФ можно записать в виде:
|
N / 2 1 |
|
N / 2 1 |
|
|
|
|||
F(k) |
x(2n) WN |
2nk |
x(2n 1) WN k(2n 1) (2.27) |
||||||
|
n 0 |
|
n 0 |
|
|
|
|
|
|
|
|
|
|
j |
2 |
2 |
j |
2 |
|
|
|
|
|
|
WN /2 |
||||
С учетом того, что |
WN2 e |
|
N |
e N /2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N / 2 1 |
|
|
N / 2 1 |
|
F(k) |
x1(n) WNnk/ 2 |
WNk |
x2(n) WNnk/ 2 , |
(2.28) |
|
|
n 0 |
k |
|
n 0 |
|
т.е. |
F(k) F (k) W |
F (k) , |
(2.29) |
||
|
1 |
N |
2 |
|
|
где F1(k) и F2(k) - N/2-точечные ДПФ последовательностей x1(n) и x2(n).
В выражении (2.29) преобразования F1(k) и F2(k) определены только
в диапазоне отсчетов k=0,N / 2 1, поэтому необходимо это выражение доопредилить до оставшихся N/2 отсчетов частоты.
ДПФ F1(k) и F2(k) являются периодическими с периодом N/2, т.е.:
F1(k) = F1(k + N/2) , а F2(k) = F2(k + N/2)

53
Кроме того, множитель WNk в (2.29), для оставшихся N/2 частотных отсчетов с учетом свойства периодичности равен:
|
j |
2 (k N /2) |
e j |
j |
2 k |
|
|
j |
2 k |
|
WN k , |
|||
|
|
|
|
|
||||||||||
e |
|
N |
|
e N |
|
e N |
||||||||
тогда можно записать: |
|
|
|
|
|
|
|
|
|
N |
|
|||
|
|
F (k) W |
k |
F (k); |
|
0 k |
-1 |
|||||||
|
|
N |
|
|||||||||||
|
|
|
1 |
|
2 |
|
2 |
(2.30) |
||||||
F(k) |
|
|
|
|
|
|||||||||
|
|
F (k) W |
k |
F (k); |
N |
k N 1 |
||||||||
|
|
N |
|
|||||||||||
|
|
|
1 |
|
2 |
|
2 |
|
|
|
|
|
||
Полученное выражение лежит в основе алгоритма БПФ по основанию 2 с прореживанием по времени.
Далее вычисления строятся по иттерационному принципу: последовательности отсчетов с четными и нечетными номерами вновь разбиваются на две части. Процесс продолжается до тех пор, пока не получится последовательность, состоящая из единственного элемента. При этом число операций умножения и сложения, необходимых для вычисления БПФ, соответственно будет равно (N/2) log2N и N log2N, а
количество базовых операций - (N/2) log2N.
Если положить: F1(k)=A, F2(k)= B, F(k)<0,N/2-1>=X, F(k)<N/2,N-1>=Y,
то граф вычисления "базовой операции" БПФ, называемой иногда «бабочка», будет иметь вид, представленный на рис.2.46.
Рис.2.46. Граф базовой операции БПФ по основанию 2 с прореживанием по времени
Рассмотрим пример построения графа 8-точечного БПФ с прореживанием по времени ( N=8=23 ):
I этап: (рис.2.47)
Входная последовательность x(n) разбивается на две последовательности x1(n) и x2(n), где x1(n) - четные, а x2(n) - нечетные члены последовательности, для которых путем двух 4-точечного ДПФ рассчитываются преобразования F1(k) и F2(k). Затем в соответствии с алгоритмом БПФ рассчитывается F(k) .

54
x(0)=x1(0) |
|
|
|
F1(0) |
|
x(2)=x1(1) |
|
|
4-точ. |
F1(1) |
|
|
|
||||
x(4)=x1(2) |
ДПФ |
F1(2) |
x(6)=x1(3) |
|
F1(3) |
x(1)=x2(0) |
|
F2(0) |
x(3)=x2(1) |
4-точ. F2(1) |
|
x(5)=x2(2) |
ДПФ |
F2(2) |
x(7)=x2(3) |
|
F2(3) |
F(0) = F1(0) + WN0 F2(0)  F(1) = F1(1) + WN1 F2(1)
F(1) = F1(1) + WN1 F2(1)  F(2) = F1(2) + WN2 F2(2)
F(2) = F1(2) + WN2 F2(2)  F(3) = F1(3) + WN3 F2(3)
F(3) = F1(3) + WN3 F2(3)
F(4) = F1(0) - WN0 F2(0)
F(5) = F1(1) - WN1 F2(1) F(6) = F1(2) - WN2 F2(2)
 F(7) = F1(3) - WN3 F2(3)
F(7) = F1(3) - WN3 F2(3)
Рис.2.47. Первый этап вычисления БПФ
II этап: (рис.2.48)
Каждая из последовательностей x1(n) и x2(n) также может быть поделена пополам. При этом две 4-точечные ДПФ будут сведены к четырем 2- точечным ДПФ.
|
|
|
|
A(0) |
F1(0)=A(0)+WN/20 B(0)= A(0)+WN0 B(0) |
|||
x(0)=x1(0)=a(0) |
|
|
2-точ. |
|||||
|
|
|
|
|
F1(1)=A(1)+WN/21 B(1)= A(1)+WN2 B(1) |
|||
x(4)=x1(2)=a(1) |
|
ДПФ |
A(1) |
|
||||
|
||||||||
|
|
|
|
B(0) |
F1(2)=A(0) - WN/20 B(0)= A(0) - WN0 B(0) |
|||
|
|
|
|
|||||
x(2)=x1(1)=b(0) |
2-точ. |
|||||||
|
|
|
F1(3)=A(1) - WN/21 B(1)= A(1) - WN2 B(1) |
|||||
x(6)=x1(3)=b(1) |
ДПФ |
B(1) |
||||||
|
|
|
|
|
|
|
|
|
x(1)=x2(0)=c(0) |
|
|
|
2-точ. |
|
|
|||
x(5)=x2(2)=c(1) |
|
ДПФ |
||
|
||||
|
|
|
|
|
x(3)=x2(1)=d(0) 2-точ. x(7)=x2(3)=d(1) ДПФ
ДПФ
C(0) |
F2(0)=C(0)+WN/20 D(0)= C(0)+WN0 D(0) |
C(1) |
F2(1)=C(1)+WN/21 D(1)= C(1)+ WN2 D(1) |
D(0)
 F2(2)=C(0) - WN/20 D(0)= C(0) - WN0 D(0)
F2(2)=C(0) - WN/20 D(0)= C(0) - WN0 D(0)
D(1) |
F2(3)=C(1) - WN/21 D(1)= C(1) - WN2 D(1) |
A, C - четные B , D - нечетные
Рис. 2.48. Второй этап вычисления БПФ
III этап : (рис.2.49)
Двухточечные ДПФ вычисляются с учетом базовой операции БПФ.

|
|
55 |
|
x(0)=a(0) |
A(0) |
= a(0) + WN/20 a(1) = a(0) + WN0 a(1) |
|
x(4)=a(1) |
A(1) = a(0) - WN/20 a(1) = a(0) - WN0 a(1) |
||
x(2)=b(0) |
B(0) |
|
|
x(6)=b(1) |
B(1) |
|
|
x(1)=c(0) |
C(0) |
a(0), b(0), c(0), d(0) - |
четные |
x(5)=c(1) |
C(1) |
a(1), b(1), c(1), d(1) - |
нечетные |
x(3)=d(0) |
D(0) |
|
|
x(7)=d(1) |
D(1) |
|
|
Рис. 2.49. Третий этап вычисления БПФ
Полный граф 8-точечной БПФ по основанию 2 и прореживанием по времени приведен на рис.2.50.
x(0) 
x(4) 
 WN0
WN0
x(2) 
x(6) 
 WN0
WN0
x(1) 
x(5) 
 WN0
WN0
x(3) 
x(7) 
 WN0
WN0
|
F(0) |
|
WN0 |
F(1) |
|
F(2) |
||
WN2 |
||
F(3) |
||
|
||
|
WN0 |
|
|
F(4) |
|
|
WN1 |
|
|
F(5) |
|
WN0 |
WN2 |
|
|
F(6) |
|
WN2 |
WN3 |
|
|
F(7) |
Рис. 2.50. Полный граф 8-точечного БПФ с прореживанием во времени
Для реализации БПФ, как видно из примера, необходимо произвести перестановку последовательности входных данных x(n). Эту перестановку можно реализовать по правилу двоичной инверсии (реверса адресов данных) (рис. 2.51).
БПФ можно реализовать не только по основанию 2, но и по основанию 4, 8, 16, а также по нечетному основанию. При этом граф БПФ будет выглядеть сложнее.

|
56 |
|
|
исх.посл. двоич.предст.адр. |
двоич.инв.адр. преобр. посл. |
||
x(0) |
000 |
000 |
x(0) |
x(1) |
001 |
100 |
x(4) |
x(2) |
010 |
010 |
x(2) |
x(3) |
011 |
110 |
x(6) |
x(4) |
100 |
001 |
x(1) |
x(5) |
101 |
101 |
x(5) |
x(6) |
110 |
011 |
x(3) |
x(7) |
111 |
111 |
x(7) |
Рис. 2.51. Реверс адресов данных перед вычислением БПФ
Если A, B и Wk - комплексные, т.е.:
A = ImA + ReA , B = ImB + ReB , Wk = ImWk + ReWk ,
то алгоритм базовой операции БПФ с прореживанием по времени будет иметь вид:
ReX = ReA + (ReB ReW - ImB ImW);
ImX = ImA + (ReB ImW + ImB ReW);
ReY = ReA - (ReB ReW - ImB ImW); ( 2.31) ImY = ImA - (ReB ImW + ImB ReW);
БПФ можно реализовать с прореживанием по частоте. Граф базовой операции представлен на рис.2.52.
Рис.2.52. Граф базовой операции БПФ с прореживанием по частоте
Сравнительное быстродействие (в мс) некоторых сигнальных процессоров при вычислении комплексного БПФ по основанию 2 с прореживанием по времени приведено в Таблице 2.3
|
|
|
Таблица 2.3 |
N |
C`25 |
C`30 |
C`40 |
128 |
0.7 |
0.37 |
0.21 |
256 |
1.9 |
0.8 |
0.46 |
512 |
4.8 |
1.74 |
1.03 |
1024 |
10.9 |
3.75 |
2.26 |

57
2.3.5. ПРИМЕР МОДЕЛИРОВАНИЯ ЦИФРОВОГО АНАЛИЗАТОРА СПЕКТРА
Модель цифрового анализатора спектра сигнала с генератором входных воздействий, составленная в приложении Simulink (MatLab), приведена на рис.2.53. В состав анализатора спектра входят:
АЦП (состоит из дискретизатора (Zero-Order Hold) и квантователя
(Quantizer));
Блок формирования аналитического сигнала (Analitic Signal);
Блок формирования выборки из N отсчетов (Buffer);
Блок БПФ (FFT);
Блок вычисления модуля спектра.
Параметры модели:
Частота дискретизации: Fs = 4000 Гц
Полоса анализа FFT: Fa = Fs/2 = 2000 Гц
Разрядность АЦП: B=10
Количество точек FFT на полосу Fs: N=512
Точность оценки частоты: F=Fs/N=4000/512=7.8 Гц
Полоса частот полезного сигнала: Fc = (700-1200) Гц.
На вход анализатора спектра подается сумма трёх синусоид (800Гц, 1000Гц и 1100Гц) с нормально распределенной помехой полосой (10-2000) Гц. Перед анализатором спектра частотная полоса ограничивается с помощью аналогового полосового фильтра (Signal Band) до (700-1200) Гц для уменьшения влияния помех. Вид сигнала с помехами в полосе (7001200) Гц показан на рис.2.54, а его спектр - на рис.2.55. В спектре видны три ярко выраженные гармоники на фоне помех.
Рис.2.53. Структурная схема модели цифрового анализатора спектра
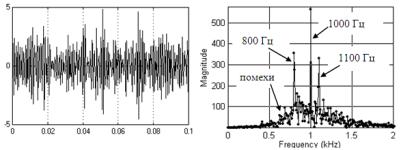
58
Рис.2.54. Сигнал с помехами |
Рис.2.55. Спектр сигнала |
на входе анализатора спектра |
с помехами в полосе анализа |
2.3.6 СООТНОШЕНИЕ МЕЖДУ ВЕЩЕСТВЕННЫМ И КОМПЛЕКСНЫМ ДПФ
Большинство алгоритмов (программ) БПФ составлены в комплексном формате. Однако, если известны отсчеты вещественного ДПФ и требуется использовать программу обратного комплексного БПФ для вычисления отсчетов во временной области х(n), надо знать, как разместить отсчеты вещественного ДПФ в формате комплексного.
В паре комплексных ДПФ
|
1 |
|
N 1 |
|
|
2 |
||
F(k) |
|
x(n) e |
|
|
|
|
|
|
|
|
|
N |
|||||
|
|
|
|
j nk |
||||
|
N |
n 0 |
|
|
|
|
|
|
|
|
N 1 |
|
2 |
||||
|
|
|
|
j |
|
|
nk |
|
x(n) F(k) e N
n 0
|
1 |
N 1 |
|
|
2 |
|
|
|
2 |
|
||||||
|
|
|
x(n) cos |
|
|
nk |
j sin |
|
|
|
nk , |
|||||
|
|
|
N |
|
N |
|||||||||||
|
|
N n 0 |
|
|
|
|
|
|
|
|
||||||
|
N 1 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||
F(k) cos |
|
|
nk |
|
j sin |
|
|
|
nk |
|||||||
N |
N |
|
||||||||||||||
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|||||
входные х(n) и выходные F(k) величины являются комплексными.
Так как реальные входные отсчеты во временной области являются вещественными и не имеют мнимой части, мнимая часть хГ(n) входных отсчетов часто принимается равной нулю или в общем случае вычисляется посредством преобразования Гильберта.
Комплексное ДПФ содержит вещественную и мнимую компоненты
ReF(k)
ImF(k)
|
1 |
|
N 1 |
|
|
|
|
|
|
|
x(n) |
|
|
|
|||
|
|
N n 0 |
|
||
|
1 |
|
N 1 |
|
|
|
|
|
|
|
x(n) |
|
|
|
|||
|
N n 0 |
|
|||
2 |
|
|
|
Г |
2 |
|
|
|
||||
cos |
|
|
nk |
x |
|
(n) sin |
|
|
nk , |
|
||
N |
|
N |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
Г |
2 |
|
|
, |
|||||
sin |
|
|
|
nk |
x |
|
|
(n) cos |
|
|
nk |
|
|
N |
|
|
N |
|
|||||||
|
|
|
|
|
|
|
|
|
||||
которые могут быть преобразованы в амплитудный и фазовый спектры

59
F(k) ReF2 (k) ImF2 (k) , (k) arctg ImF(k) .
ReF(k)
Вещественное ДПФ является упрощением комплексного. Оно использует только вещественные отсчеты х(n), однако результат вычисления вещественного ДПФ является комплексным. Вещественная и мнимая части вещественного ДПФ равны:
2 |
N 1 |
|
2 |
|
2 |
N 1 |
|
2 |
|
,k 0,N |
2 . |
|||
ReF(k) |
|
|
x(n) cos |
|
nk , ImF(k) |
|
|
x(n) sin |
|
nk |
||||
|
N |
|
N |
|||||||||||
|
N n 0 |
|
|
N n 0 |
|
|
|
|
||||||
Обратное вещественное ДПФ вычисляется следующим образом:
N /2 |
|
2 |
|
2 |
|
|||
x(n) |
ReF(k) cos |
|
nk |
ImF(k) sin |
|
nk . |
||
N |
N |
|||||||
n 0 |
|
|
|
|
||||
Примечание:
Перед использованием уравнения для вычисления отсчетов во временной области х(п), значения ReF(0) и ReF(N/2) должны быть поделены на два.
Пусть входные данные представляют собой N 16 вещественных (рис.1) и комплексных (рис.2) отсчетов x(n) .
Вещественное ДПФ дает вещественные и мнимые значения F(k), где k находится в диапазоне от 0 до N/2. При этом мнимые отсчеты ImF(0) и ImF(N/2) всегда равны 0.
Результат вычислений ДПФ F(k) соответствует частотному диапазону, равному половине частоты дискретизации fд (от 0 до N/2). Шаг по частоте (точность оценки частоты) равен fд /N.
Комплексное ДПФ имеет вещественные и мнимые значения и на входе, и на выходе. Заштрихованные области соответствуют отсчетам, которые являются общими и для вещественного, и для комплексного ДПФ.
На рис.3 подробно показано соотношение между комплексным и вещественным ДПФ.
В рассматриваемом примере комплексное ДПФ вычисляется по N=16 вещественным отсчетам х(п). Мнимая часть отсчетов хГ(п) принята равной нулю.

60
рис.1 Исходные данные и результаты вычисления вещественного ДПФ
рис.2 Исходные данные и результаты вычисления комплексного ДПФ
Отсчеты вещественного ДПФ располагаются в диапазоне от 0 до N/2, причем значения ImF(0) и 1mF(N/2) всегда равны 0. Отсчеты между N/2 и (N-1) содержат «отрицательные» частоты в комплексном ДПФ.
