Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный морской технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Аналитиченская_геометрия.pdf

Скачиваний:

Добавлен:

18.04.2015

Размер:

783.04 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2211 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

виде a = x i + y j					где x, y - его координаты в стандартном ортонормированном базисе
	1	,		0	и изображать направленным отрезком OM , начало которого может
i =		,	j =
	0			1
	0			1

быть перенесено в любую точку плоскости (рис.14).

Рис.14.

Расстояние

r между точками M1(x1,

y1) и M2 (x2 , y2 )

определяется по формуле

r =

(x − x )2

+ (y

− y

)2 .

Координаты точки

(x , y

), делящей отрезок

M M

в отношении λ =

M1M0

M0M2

отыскиваются по формулам:

x1 + λx2

1 + λ .

y1 + λy2

1 + λ

2.2.

Линии на плоскости. Прямая на плоскости

Определение

f (x , y )= 0 является уравнением линии Φ на плоскости,

Алгебраическое уравнение

если:

1.Для любой точки M0 (x0 , y0 ) Φ f (x0 , y0 )= 0 .

2.Для любого решения x0 , y0 уравнения f (x , y )= 0 точка M0 (x0 , y0 ) Φ.

ЗАМЕЧАНИЕ 1

Из определения следует, что линия на плоскости задается алгебраическим уравнением, связывающим координаты тех и только тех точек, которые принадлежат этой линии.

Теорема

Линейное уравнение с двумя переменными A x + B y +C = 0 задает на плоскости прямую.

Доказательство

Линейное уравнение с двумя неизвестными имеет бесконечно много решений. Пусть x0 , y0 и x1 , y1 любые два решения этого уравнения. Из определения уравнения линии

следует, что точки M0 (x0 , y0 ) и M1(x1, y1) принадлежат данной линии, то есть, справедливы равенства

A x0 + B y0 +C = 0 и

A x1 + B y1 + C = 0.

Вычитая из первого равенства второе, получим

A(x1 − x0 )+ B ( y1 − y0 )= 0.

x1	− x0	r		A	, то последнее уравнение
Если рассмотреть векторы r =		и n	=		, то последнее уравнение
	− y0
y1	− y0			B
эквивалентно векторному уравнению	(rv, n)= 0.		Это	означает, что любой вектор с

началом и концом на данной линии ортогонален вектору n . Ясно, что такому условию удовлетворяют только точки, лежащие на прямой.

ЗАМЕЧАНИЕ 2

Из доказательства теоремы следует геометрический смысл коэффициентов A и B . Это координаты перпендикулярного ей вектора n .

Вектор nr называется нормальным вектором, а уравнение A x + B y +C = 0 - общим

уравнением прямой.

В зависимости от задания прямой, такое уравнение может быть записано в различных видах.

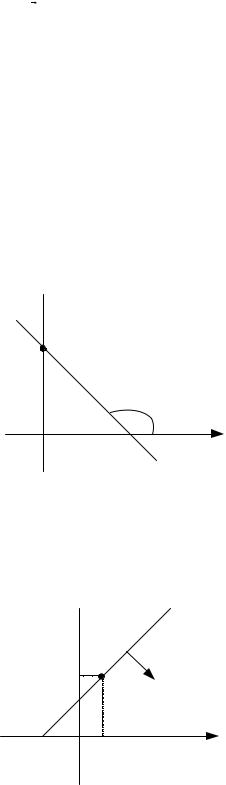
Уравнение прямой с угловым коэффициентом y

Рис. 15

Уравнение y = kx +b , где угловой коэффициент k = tg α, α- угол между прямой и осью Ox , b - ордината точки пересечения прямой с осью Oy (рис.15), называется

уравнением прямой с угловым коэффициентом.

Уравнение прямой с нормальным вектором y

M 0	n
y0
x0	x
Рис. 16

Уравнение A ( x − x0 )+ B ( y − y0 )= 0, где M0 (x0 , y0 ) - точка, принадлежащая

	A	- нормальный вектор прямой (любой вектор,
прямой (рис.16), n =		- нормальный вектор прямой (любой вектор,

	B

перпендикулярный данной прямой), называется уравнением прямой с нормальным вектором.

Каноническое уравнение прямой

M 0
y0
x0	x
	x
Рис. 17.

Уравнение			x − x0		=	y − y0	, где	M 0 (x0 , y0 ) -	точка, принадлежащая прямой
			m			n

(рис.17),		m		-	направляющий			вектор прямой	(любой вектор, параллельный
	s =

		n

прямой), называется каноническим уравнением прямой.

Уравнение прямой в «отрезках»

Рис. 18

Уравнение ax + by =1, где a - абсцисса точки пересечения прямой с осью Ox , b -

ордината точки пересечения прямой с осью Oy (рис.18), называется уравнением прямой в отрезках.

Угол между прямыми

y
α2	ϕ	α1
		x
	Рис. 19

Если	k1 и	k2 -	угловые коэффициенты двух прямых, то угол ϕ между ними
находится по формуле:
		tg ϕ = tg(α1 − α2 )=		tg α1 − tg α2	=	k1 − k2	,
		tg ϕ = tg(α1 − α2 )=			=		,
			1+ tg α1 tg α2			1+ k1k2
где α1 и	α2	- углы,	которые данные прямые составляют с координатной осью Ox
(рис.19).

ЗАМЕЧАНИЕ

Если прямые заданы общими уравнениями A x1 + B1 y +C1 = 0

и A2 x + B2 y + C2 = 0, то угол между ними можно определять как

угол между их нормальными векторами n		A	и n			A
угол между их нормальными векторами n	=	1	и n	2	=		2	.
1	B			2	B		2
		1					2

Точку	пересечения	двух	прямых,	заданных				общими	уравнениями,
A x1 + B1 y + C1 = 0 и A2 x + B2 y + C2 = 0, находят, решая систему:
		A x1 + B1 y + C1 = 0
		A x2 + B2 y + C2 = 0.
Задача 1
Напишите уравнения		высоты	из вершины		A	и	медианы из		вершины	B	в
треугольнике ABC , если заданы его вершины A(−1,−5), B (3,−1) и C (1,−2).
Решение
Для высоты AK используем			уравнение	прямой		с	нормальным		вектором,	где	в
качестве нормального вектора n возьмем вектор					BC .		Для медианы		BM используем
каноническое уравнение прямой,			где в качестве		направляющего вектора s возьмем

вектор BM (рис.20).

B K