
- •7. Интегральное исчисление функций одной переменной (24 часа)
- •1. Неопределённый интеграл
- •1.1. Первообразная и неопределённый интеграл
- •1.2. Основные свойства неопределённого интеграла
- •1.3. Таблица неопределённых интегралов
- •1.4. Интегрирование методом замены переменной
- •1.5. Интегрирование по частям
- •Интегралы, берущиеся "по частям"
- •1.6. Интегрирование простейших рациональных дробей
- •1.7. Интегрирование рациональных дробей
- •1.8. Интегрирование некоторых иррациональных выражений
- •1.9. Интегрирование некоторых классов тригонометрических функций
- •2. Определенный интеграл
- •2.1. Понятие определенного интеграла
- •Геометрический смысл определенного интеграла
- •2.2. Основные свойства определенного интеграла
- •2.3. Определенный интеграл, как функция верхнего предела. Теорема Барроу
- •2.4. Формула Ньютона – Лейбница
- •2.5. Замена переменной в определенном интеграле
- •2.6. Интегрирование по частям в определенном интеграле
- •2.7. Геометрические приложения определенного интеграла
- •2.8. Несобственные интегралы
- •7. Интегральное исчисление функций одной переменной (18 часов)
- •Основная
- •Дополнительная

2.7.Геометрические приложения определенного интеграла
•Вычисление площадей
1. Если f (x) ≥ 0 на [а;b], то площадь криволинейной трапеции, ограниченной
b
кривой y = f (x) , осью Ox и прямыми x = a и x = b (рис. 6), равна: S = ∫ f (x)dx . a
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6 |
|
|
|
|
f (x) ≤ 0 на [а;b] |
|
b |
||||
2. |
Если |
, то определенный интеграл ∫ f (x)dx ≤ 0 и по |
|||||||
|
|
|
|
|
|
|
|
|
a |
абсолютной величине равен площади соответствующей криволинейной трапеции S (рис. |
|||||||||
|
|
b |
|
|
b |
|
|
||
|
|
|
|
|
|||||
7), т.е. S = |
∫ f (x)dx |
|
= −∫ f (x)dx . |
|
|
||||
|
|
a |
|
|
a |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7
3. Если f (x) конечное число раз меняет свой знак на отрезке [а;b], то интеграл по всему отрезку [а;b] разбиваем на сумму интегралов по частичным отрезкам (рис. 8), или
b
S = ∫ f (x) dx .
a
y = f (x)
a |
b |
x |
|
|
Рис. 8.
Пример. Вычислить площадь криволинейной трапеции, ограниченной графиком функции y = sin x , на промежутке x [0; 2π] (рис. 9).
y 
O |
x |
Рис. 9.
25

π |
|
2π |
|
|
|
0π + |
|
|
π2π |
|
|
|
|
|
|
|
|||||||||||||
S = ∫sin x dx + |
|
∫sin x dx |
|
=−cos x |
|
(−cos x) |
|
= 2 + |
|
− 2 |
|
= 4 , или |
||
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||
0 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
π
S = 2∫sin x dx = 4 .
0
4.Если кривая задана уравнениями в параметрической форме (рис.10): х = ϕ(t) и
y = ψ(t) , где α ≤ t ≤ β и ϕ(α) = a; ϕ(β) = b .
Рис. 10 Тогда площадь криволинейной трапеции вычисляется через определенный интеграл, в котором следует провести замену переменных.
b b
S = ∫ f (x)dx = ∫ydx =
a a
y = ψ(t) x = ϕ(t)
dx = ϕ′(t) dt x = a; t = α x = b; t = β
β
= ∫ψ(t)ϕ′(t)dt.
α
β
S = ∫ψ(t)ϕ′(t)dt.
|
α |
5. |
Если кривая задана в полярной системе координат уравнением ρ = ρ(ϕ) , и если |
требуется вычислить площадь сектора, соответствующего центральному углу α ≤ ϕ ≤ β, то можно получить формулу для площади этого сектора.
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
ϕ |
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
θ |
|
|
|||||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||
|
|
|
|
|
|
|
= |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
ϕ |
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
||
|
|
|
|
|
|
ϕ |
|
|
|
|
ϕ |
i |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
ϕ |
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
ϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
ϕ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
= |
ϕ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ = α |
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Рис. 11 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на n частей лучами: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Разобьем |
площадь криволинейного |
|
|
сектора |
|
|||||||||||||||||||
ϕ0 = α, ϕ1, ϕ2 ,...., ϕi−1, ϕi ,..., ϕn = β (рис. 11). В каждом частном угле |
ϕi |
возьмем луч |
|||||||||||||||||||||||
θi и найдем ρ(θi ) . Тогда площадь криволинейного сектора с углом |
ϕi |
будет равна |
|||||||||||||||||||||||
S |
i |
= 1 (ρ(θ ))2 |
ϕ . Следовательно, |
|
площадь всего |
«ступенчатого» |
сектора будет |
||||||||||||||||||
|
2 |
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
||

равна S |
|
= |
1 |
n |
2 |
ϕ |
. Получили интегральную сумму S |
|
. Переходя к пределу при |
|||||
n |
|
∑(ρ(θ )) |
n |
|||||||||||
|
|
2 i=1 |
i |
i |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
max ϕi |
→ 0 , получим Sn → S . Таким образом площадь сектора равна |
|||||||||||||
(n→∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
β |
|
|
|
|
|
|
|
|
|
|
|
|
Sсектора = |
∫ρ2 (ϕ)dϕ |
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
Пример. |
Вычислить |
площадь фигуры, ограниченной |
|
лемнискатой Бернулли |
||||||||||
ρ = a сos 2ϕ (рис. 12). |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S′
x
Рис. 12
S = 4S |
′ = |
4 |
1 |
π4 |
a |
2 |
cos 2ϕdϕ =2a |
2 |
π4 |
cos 2ϕdϕ = 2a |
2 sin 2ϕ |
|
π4 |
== 2a |
2 |
1 |
(1 −0) |
= a |
2 |
. |
||
|
||||||||||||||||||||||
2 |
∫ |
|
|
∫ |
2 |
|
|
0 |
|
2 |
|
|||||||||||
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
• Вычисление объема тела по площадям параллельных сечений |
|
|
|||||||||||||||||||
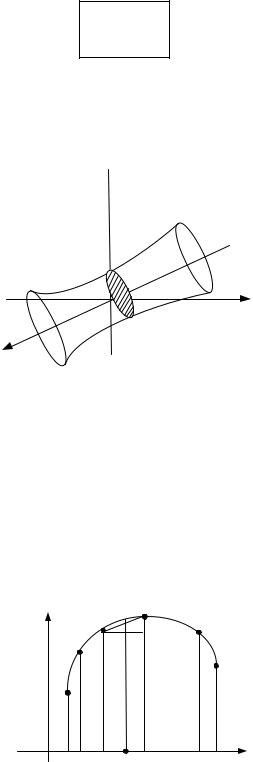
Пусть |
T |
- некоторое тело, |
расположенное вдоль оси |
Ox . |
Предположим, |
что для |
||||||||||||||||
любого х (а; b) известна S = S(x) |
― площадь любого сечения этого тела плоскостью, |
|||||||||||||||||||||
перпендикулярной оси Ox (рис. 13).
S(xi−1 ) S(ξi ) S(xi )
|
a |
xi−1 |
|
ξ |
|
xi |
b |
|
|
||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предположим, что S(x) |
|
|
Рис. 13. |
|
|
x . Проведем |
|
||||
есть непрерывная |
функция от |
плоскости |
|||||||||
x = a, x = x1, ..., x = xn = b . Эти плоскости разобьют тело T на п слоев. |
|
||||||||||
В каждом частичном промежутке [xi−1; xi ] возьмем произвольную точку ξi |
[xi−1; xi ] |
||||||||||
и построим цилиндрическое тело, образующая которого параллельна оси Ox , а направляющая представляет собой контур сечения тела T плоскостью x = ξi .
Объем такого цилиндра равен S(ξi ) xi , где S(ξi ) - площадь поперечного сечения
n
цилиндра, xi - его высота. Сумма объемов всех цилиндров равна Vn = ∑S(ξi ) xi . i=1
27
Vn представляет собой интегральную сумму для непрерывной функции S(x) на отрезке
[a;b]. Следовательно, существует конечный предел этой интегральной суммы, который по определению равен определенному интегралу.
b
V = ∫S(x)dx.
a
• Объем тела вращения
Рассмотрим тело, образованное вращением вокруг оси Ox непрерывной на [a;b] кривой y = f (x) и ограниченное плоскостями x = a и x = b . Такое тело называется телом вращения (рис. 14).
z 
|
|
) |
|
( |
|
f |
x |
|
= |
|
|
y |
|
|
y
x
Рис. 14
В этом случае произвольное сечение тела плоскостью, перпендикулярной оси Ox ,
есть круг, площадь которого равна: S = πy2 = π( f (x))2 . Тогда объем тела вращения равен
b |
b |
b |
|
V = ∫S(x)dx = ∫π(f (x))2 dx |
V = π∫(f (x))2 dx |
. |
|
a |
a |
a |
|
• Длина дуги в декартовых координатах
Определение. Под длиной дуги AB понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной возрастает непрерывно, а длина наибольшего звена ее стремится к нулю.
y
Mi |
si Mi |
M |
|
1 |
yi |
||
− |
n−1 |
||
M1 |
|
||
|
xi |
|
|
|
|
|
B |
A |
|
|
|
|
ξ |
xi....... xn−1b x |
|
a x1...xi−1i |
|||
Рис. 15. n
То есть, если длина ломаной равна Sn = ∑ Si , то длина дуги AB (рис. 15) равна i=1
n
S = lim ∑ Si .
max Si →0 i=1
28

|
Теорема. |
Если y = f (x) |
непрерывна на [a;b] и имеет непрерывную производную |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
lim |
∑ Si |
= S . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
f (x) на [a;b], то существует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
max |
Si →0 i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Доказательство. |
Пусть |
yi - |
|
приращение |
данной |
функции |
y = f (x) |
на |
отрезке |
||||||||||||||||||||
[x |
−1 |
; x ]. По теореме Пифагора имеем |
S |
i |
= |
|
( |
x )2 + |
( y )2 . |
|
|
|
|
|
|
|
|
|
||||||||||||
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
||||
Применяя |
|
теорему |
Лагранжа, |
получим |
|
yi = f (xi ) − f (xi−1) = |
xi f ′(ξi ) где |
|||||||||||||||||||||||
ξi |
[xi−1; xi ]. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Si = ( xi )2 + ( xi )2 (f ′(ξi ))2 = xi 1 + (f ′(ξi ))2 . |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
Т.о. |
длина |
вписанной |
ломаной |
равна |
|
Sn |
= ∑ xi 1 + (f ′(ξi ))2 . |
Так |
|
как |
f ′(x) - |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|||
непрерывна, |
то Sn представляет собой интегральную сумму для непрерывной функции |
|||||||||||||||||||||||||||||
|
|
′ |
2 |
. Следовательно, предел этой интегральной суммы существует и равен |
|
|||||||||||||||||||||||||
1 + (f (x)) |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + (f ′(ξi )) |
|
|
|
|
b |
|
|
′ |
|
|
|
|
|
|
|
|||||
|
|
|
|
S = maxlimx |
|
∑ xi |
|
2 |
|
S |
= ∫ |
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
→0 |
|
|
1 + (f (x)) dx |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
i |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
ЗАМЕЧАНИЯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
а) Если верхний предел интегрирования считать переменным и обозначить через x , то |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
2 |
|
|
|
|
|
|
длина |
|
дуги |
S |
будет |
|
функцией |
от |
x : |
S(x) = ∫ |
|
|
′ |
dx. |
Тогда |
||||||||||||||
|
|
|
|
1 + (f (x)) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
S′(x) = 1 + (f |
|
|
|
|
dS |
|
|
|
dy |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
или |
= |
1 + |
dS = |
|
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||
|
|
′(x)) |
|
|
|
|
|
|
(dx) |
+(dy) . |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Получили формулу для дифференциала дуги dS . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
б) Если кривая задана параметрически, |
|
|
|
x = ϕ(t) |
, где |
α ≤ t ≤ β |
|
|
, |
|||||||||||||||||||
|
|
то есть |
|
|
ϕ(α) = a |
ϕ(β) = b |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ψ(t) |
|
|
|
|||||||||
то в интеграле для длины дуги кривой следует сделать замену переменных.
b
S = ∫ 1 + (y′x )2 dx
1 + (y′x )2 dx
a
β
= ∫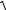 (ϕ′t )2 + (ψ′t
(ϕ′t )2 + (ψ′t
α
y = ψ(t) |
|
|
|
|
|
|
|
|||
x = ϕ(t) |
|
|
|
|
2 |
|
|
|||
dx |
= ϕ′(t) dt |
|
β |
|
′ |
|
|
|||
|
|
′ |
|
|
|
ψ (t) |
|
′ |
||
= y′ |
= |
ψ |
(t) |
= |
∫ |
|
||||
′ |
|
1 + |
′ |
|
ϕ (t)dt = |
|||||
x |
|
|
|
α |
|
|
|
|
||
|
|
ϕ (t) |
|
ϕ (t) |
|
|
||||
x = a; t |
= α |
|
|
|
|
|
|
|
||
x = b; t |
= β |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
)2 dt |
|
β |
|
(ϕ′t )2 + (ψ′t )2 dt |
|
|||||
S = ∫ |
|
. |
||||||||
|
|
|
|
α |
|
|
|
|
|
|
в) Замена переменных проводится и в том случае, когда кривая задана в полярных
координатах, |
то есть |
ρ = ρ(ϕ) , где |
α ≤ ϕ ≤ β. |
Переходя к переменным |
ρ |
|
и |
ϕ по |
||
формулам перехода |
от полярных координат к |
x = ρcos ϕ |
, |
получим |
||||||
декартовым |
ϕ |
|||||||||
|
|
|
|
|
y = ρsin |
|
|
|
|
|
x = ρ(ϕ) cos ϕ |
, при |
α ≤ ϕ ≤β. В |
|
xϕ′ = ρ′cos ϕ−ρsin ϕ |
|
, |
а |
тогда |
||
|
|
этом случае |
|
|
||||||
y = ρ(ϕ) sin ϕ |
|
|
|
yϕ′ = ρ′sin ϕ+ρcos ϕ |
|
|
|
|||
|
|
|
|
29 |
|
|
|
|
|
|

β |
2 |
′ 2 |
|
β |
|
2 |
|
|
2 |
′ |
dϕ = ∫ |
′ |
|
′ |
|||||
S = ∫ (xϕ ) |
+ (yϕ ) |
(ρ cos ϕ−ρsin ϕ) |
+ (ρ sin ϕ+ρcos ϕ) dϕ = |
||||||
α |
|
|
|
α |
|
|
|
|
|
= β∫ (ρ′)2 +ρ2 dϕ |
β |
(ρ′(ϕ))2 + (ρ(ϕ))2 dϕ |
|
|
|||||
S = ∫ |
. |
|
|||||||
α |
|
|
|
α |
|
|
|
|
|
Пример. Найдите длину кардиоиды ρ = a(1 + cos ϕ) (рис. 16).
y 
S′
 x
x
π |
|
|
Рис. 16 |
|
|
π |
|
S = 2S′ = 2∫ |
(−a sin ϕ)2 |
+ a2 |
(1 + cos ϕ)2 dϕ = 2∫ 2a2 + 2a2 cos ϕ dϕ = |
0 |
|
|
0 |
= 2 |
π |
|
π |
ϕ dϕ = 4a 2sin |
|
|
π |
|
2 a ∫ 2 cos2 |
ϕdϕ = 2 2a∫cos |
ϕ |
= 8a . |
|||||
|
0 |
|
2 |
0 |
2 |
2 |
0 |
|
|
|
• |
Поверхность тела вращения |
|
|
|
||
Пусть f (x) |
′ |
|
|
|
|
|
|
|
и f (x) - непрерывны на [a;b]. Определим площадь поверхности, |
||||||||
образованной вращением кривой y = f (x) |
вокруг оси Ox на отрезке [a;b] (рис. 17). |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 17
Каждая хорда длины Si при вращении опишет усеченный конус, поверхность которого Pi равна
Pi |
= 2π |
yi−1 + yi |
Si = 2π |
yi−1 + yi |
xi |
1 + (f ′(ξi ))2 . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
xi → 0 , т.е. |
2 |
|
|
|
|
|
|
|
|
|
|
|||
Перейдем к пределу при max |
|
|
|
|
|
|
|
|
|
|
|
|||||||
P = |
lim |
|
π∑n [f (xi−1) + f (xi )] |
|
xi |
1 + (f ′(ξi ))2 = |
|
|
|
|
||||||||
|
max xi →0 |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
x 1 + (f ′(ξ |
2 |
|
|
P = 2π |
b |
|
′ |
2 |
dx |
|
|||||
= lim 2π∑ f (ξ |
) |
, или |
|
|
|
. |
||||||||||||
)) |
|
∫ |
f (x) 1 + (f (x)) |
|||||||||||||||
max xi →0 |
|
i |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||
30
