
- •7. Интегральное исчисление функций одной переменной (24 часа)
- •1. Неопределённый интеграл
- •1.1. Первообразная и неопределённый интеграл
- •1.2. Основные свойства неопределённого интеграла
- •1.3. Таблица неопределённых интегралов
- •1.4. Интегрирование методом замены переменной
- •1.5. Интегрирование по частям
- •Интегралы, берущиеся "по частям"
- •1.6. Интегрирование простейших рациональных дробей
- •1.7. Интегрирование рациональных дробей
- •1.8. Интегрирование некоторых иррациональных выражений
- •1.9. Интегрирование некоторых классов тригонометрических функций
- •2. Определенный интеграл
- •2.1. Понятие определенного интеграла
- •Геометрический смысл определенного интеграла
- •2.2. Основные свойства определенного интеграла
- •2.3. Определенный интеграл, как функция верхнего предела. Теорема Барроу
- •2.4. Формула Ньютона – Лейбница
- •2.5. Замена переменной в определенном интеграле
- •2.6. Интегрирование по частям в определенном интеграле
- •2.7. Геометрические приложения определенного интеграла
- •2.8. Несобственные интегралы
- •7. Интегральное исчисление функций одной переменной (18 часов)
- •Основная
- •Дополнительная
Можно доказать, что функция является интегрируемой отрезке [а;b], если этот отрезок модно разбить на конечное число отрезков, на которых данная функция непрерывна.
2.2. Основные свойства определенного интеграла
10. Постоянный множитель можно выносить за знак определенного интеграла, т.е.
b |
b |
|
|
|
|
|
|
|
∫Af (x)dx = A∫ f (x)dx , A = const , если эти интегралы существуют. |
||||||||
a |
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
n−1 |
|
|
|
Действительно, ∫Af (x)dx = |
lim |
∑Af (ξi ) xi = |
|
||||
|
|
a |
|
max |
xi |
→0 i=0 |
|
|
|
|
|
n−1 |
|
xi = A lim |
n−1 |
b |
|
|
lim |
|
A ∑ f (ξi ) |
∑ f (ξi ) |
xi = A∫ f (x)dx . |
|||
|
max xi |
→0 |
i=0 |
|
|
max xi |
→0 i=0 |
a |
20. Определенный интеграл от суммы нескольких функций равен сумме интегралов от слагаемых, т.е.
|
|
|
b |
|
|
|
b |
|
b |
|
|
|
|
|
|
∫( f1(x) + f2 (x))dx = ∫ f1(x)dx + ∫ f2 (x)dx |
|
|
|||||||
|
|
|
a |
|
|
|
a |
|
a |
|
|
|
если f1 (х) и |
f2 (х) - интегрируемые на [а;b] |
функции. |
|
|
|
|||||||
|
b |
|
|
|
|
|
n−1 |
|
|
|
|
|
Так как ∫( f1(x) + f2 (x))dx = |
lim |
∑( f1 (ξi ) + f2 (ξi )) |
xi = |
|
|
|||||||
|
a |
|
|
max xi →0 i=0 |
|
|
|
|
|
|||
|
|
|
n−1 |
|
|
|
n−1 |
|
b |
b |
|
|
= |
lim |
∑ f1(ξi ) xi + |
lim |
∑ f2 (ξi ) xi = ∫ f1 (x)dx + ∫ f2 (x)dx . |
|
|||||||
|
max |
xi →0 i=0 |
|
max |
xi |
→0 i=0 |
|
a |
a |
|
|
|
30. Если |
на |
отрезке [а;b], |
где |
а < b , |
интегрируемые |
функции |
f (x) и |
g(x) |
||||
|
|
|
|
|
|
|
b |
|
b |
|
|
|
удовлетворяют условию |
f (x) ≤ g(x) , то ∫ f (x)dx ≤ ∫g(x)dx . |
|
|
|
||||||||
|
|
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
b |
|
b |
b |
|
|
Доказательство. Рассмотрим разность ∫g(x)dx − ∫ f (x)dx = ∫(g(x) − f (x))dx . |
||||||||||||
|
|
|
|
х [а; b], |
a |
|
a |
a |
|
|
||
Так как |
g(х) − f (х) ≥ 0 |
то, по |
геометрическому смыслу |
определенного |
||||||||
|
b |
|
|
|
|
b |
|
b |
|
|
|
|
интеграла, ∫(g(x) − f (x))dx ≥ 0 |
∫ f (x)dx ≤ ∫g(x)dx . |
|
|
|
||||||||
|
a |
|
|
|
|
a |
|
a |
|
|
|
|
40. Если m и M - наименьшее и наибольшее значения непрерывной функции |
f (x) |
|||||||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
на отрезке [а;b] и а ≤ b , то m(b − a) ≤ ∫ f (x)dx ≤ M (b − a) . |
|
|
|
|||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
Доказательство. По условию m ≤ f (x) ≤ M , тогда ∫mdx ≤ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
|
b |
b |
|
|
|
n−1 |
|
|
|
∫Mdx . |
|
Но |
∫mdx = m∫dx = m |
lim |
∑ xi = m(b − a) . |
Аналогично, |
||||||
a |
|
|
|
a |
a |
|
max xi |
→0 i=0 |
|
|
|
|
b
∫Mdx = M (b − a) .
a
19
b
Тогда m(b − a) ≤ ∫ f (x)dx ≤ M (b − a) и теорема доказана.
a
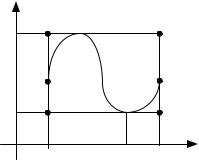
Доказанное свойство определенного интеграла имеет наглядную геометрическую интерпретацию. Если f (x) ≥ 0 , то SaA1B1b ≤ SaABb ≤ SaA2 B2b (рис. 3).
y |
A2 |
B2 |
|
M |
|||
|
|
y = f (x)
|
A |
|
B |
m |
A1 |
|
B1 |
|
|
||
|
a |
b |
x |
Рис. 3
50. Теорема о среднем. Если f (x) - непрерывна на отрезке [а;b], то существует точка ξ [а;b] такая, что справедливо равенство
b
∫ f (x)dx = (b − a) f (ξ) .
a
|
Доказательство. Пусть для определенности |
а < b . |
Непрерывная на отрезке [а;b] |
|||||||||||||||
функция |
f (x) |
ограничена на нем. Пусть m ≤ f (x) ≤ M . Тогда |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(b − a) ≤ ∫ f (x)dx ≤ M (b − a) . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
b |
|
|
Разделив это равенство на (b − a) , |
получим m ≤ |
|
∫ f (x)dx≤ M . Если обозначить |
|||||||||||||||
b − a |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx = μ, то m ≤ μ ≤ M . |
|
|
|
|
|
|
|||||||||||
|
b − a |
|
|
|
|
|
|
|||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Так как |
f (x) |
- непрерывна, то она принимает все значения, заключенные между |
|||||||||||||||
числами |
|
m |
|
и |
M . |
Следовательно, ξ [a;b], |
такое, что f (ξ) = μ, т.е. |
|||||||||||
|
|
|
|
|
1 |
|
|
b |
|
|
|
|
|
|
|
b |
|
|
|
f (ξ) = |
|
|
|
∫ f (x)dx . Из последнего равенства следует ∫ f (x)dx = (b − a) f (ξ) , где |
|||||||||||||
|
b − a |
|||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|||||
|
ξ [a;b]. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
a |
|
|
|
60. Из определения определенного интеграла ∫ f (x)dx = −∫ f (x)dx . |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
b |
|
|
70. |
|
|
Для |
|
любых |
трех |
чисел |
a, b, c |
справедливо |
равенство |
||||||||
|
b |
|
|
|
c |
|
|
b |
|
|
|
|
|
|
|
|||
|
∫ f (x)dx |
= ∫ f (x)dx + ∫ f (x)dx , если только все три интеграла существуют. |
|
|||||||||||||||
|
a |
|
|
|
a |
|
|
c |
|
|
|
|
|
|
|
|||
Доказательство.
20
Разобьем [а;b] на части так, чтобы точка c была точкой деления. Затем, разобьем
|
b |
|
|
|
|
c |
интегральную сумму ∑ , соответствующую отрезку [а;b], на две суммы: |
∑ - сумму, |
|||||
|
a |
|
|
|
|
a |
соответствующую [а;c] |
b |
|
|
|
|
|
и ∑ - сумму, соответствующую [c;b]. Тогда |
|
|||||
|
|
c |
|
|
|
|
|
b |
|
c |
b |
xi . |
|
|
∑ f (ξi ) xi = ∑ f (ξi ) |
xi + ∑ f (ξi ) |
|
|||
|
a |
|
a |
c |
|
|
Переходя к пределу при max xi |
→ 0 , получим |
|
|
|
||
|
|
b |
c |
b |
|
|
|
|
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx . |
|
|
||
|
|
a |
a |
c |
|
|
Если же, например, |
a < b < c , то на основании доказанного свойства определенного |
|||||
|
|
|
|
c |
b |
c |
интеграла |
справедливо |
равенство: |
∫ f (x)dx |
= ∫ f (x)dx + ∫ f (x)dx |
||
|
|
|
|
a |
a |
b |
b |
c |
c |
|
|
|
|
∫ f (x)dx |
= ∫ f (x)dx − ∫ f (x)dx |
. Тогда по свойству 60: |
|
|
||
a |
a |
b |
|
|
|
|
|
|
b |
c |
b |
|
|
|
|
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx . |
|
|
||
|
|
a |
a |
c |
|
|
Аналогично доказывается это свойство при другом расположении точек a,b,c .
2.3. Определенный интеграл, как функция верхнего предела. Теорема Барроу
|
|
|
|
|
[а;b]. |
|
x |
Пусть |
f (x) |
- |
непрерывна |
на |
Рассмотрим |
интеграл ∫ f (t)dt , где |
|
t [a; x] [a;b] |
|
|
|
|
|
a |
|
(во |
избежание |
путаницы, |
переменная интегрирования обозначена |
||||
другой буквой). |
|
a этот интеграл |
|
|
|
||
При постоянном |
будет |
представлять |
собой функцию верхнего |
||||
|
|
|
|
|
|
x |
|
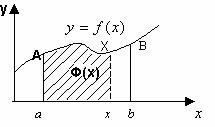
предела x . Эту функцию мы обозначим через Φ(x) = ∫ f (t)dt . |
|||||||
|
|
|
|
|
|
a |
|
Если |
f (x) ≥ 0 , то величина Φ(x) численно равна площади криволинейной трапеции |
||||||
aAXx (рис. 4). Очевидно, что эта площадь изменяется в зависимости от x .
Рис. 4.
x
Теорема Барроу. Если f (x) - непрерывная функция и Φ(x) = ∫ f (t)dt , то Φ(x)
a
дифференцируемая функция и ее производная равна
21

|
x |
′ |
|
|
′ |
|
|
|
|
= ∫ f (t)dt = f (x) . |
|
|||
Φ (x) |
|
|||
|
a |
|
|
|
Доказательство. Дадим x приращение |
x , тогда |
|
|
|
x+ |
x |
x |
x+ x |
|
Φ(x + x) = ∫ f (t)dt = ∫ f (t)dt + ∫ f (t)dt . |
|
|||
a |
|
a |
x |
|
Найдем приращение ΔΦ : |
|
|
|
|
x+ x |
x |
x |
x+ x |
x |
ΔΦ = Φ(x + x) −Φ(x) = ∫ f (t)dt − ∫ f (t)dt = ∫ f (t)dt + ∫ f (t)dt − ∫ f (t)dt . |
||||
a |
a |
a |
x |
a |
x+ x
Таким образом ΔΦ = ∫ f (t)dt . Применим к этому интегралу теорему о среднем (рис.5):
x
x+ x
ΔΦ = ∫ f (t)dt = f (ξ)(x + x − x) =
x
|
′ |
ΔΦ |
= lim |
Найдем Φ (x) = lim |
x |
||
|
x→0 |
x→0 |
|
то lim |
f (ξ) = lim f (ξ) = f (x) |
||
x→0 |
ξ→x |
|
|
f (ξ) x , где ξ [x; x + x]
Рис. 5 |
|
|
|
f (ξ) x |
= |
lim |
f (ξ) . Так как ξ → x при x → 0 , |
|
|||
x |
x→0 |
|
|
вследствие |
непрерывности. Следовательно, |
||
Φ′(x) = f (x) .
2.4. Формула Ньютона – Лейбница
Теорема. Если F(x) есть какая-либо первообразная для функции f (x) , непрерывной на [а;b], то справедлива формула
b
∫ f (x)dx = F(b) − F(a) ,
a
которая называется формулой Ньютона – Лейбница.
|
|
|
|
|
|
x |
Доказательство. |
Пусть y = F(x) - |
первообразная |
для f (x) . Но ∫ f (t)dt - тоже |
|||
|
|
|
|
′ |
|
a |
|
|
x |
|
|
|
|
первообразная для |
f (x) , так как |
|
|
|
= f (x) . |
Эти первообразные отличаются |
∫ f (t)dt |
|
|||||
|
|
a |
|
|
|
|
x
на произвольную постоянную, т.е. ∫ f (t)dt = F(x) +C . a
22
