
- •РАБОЧАЯ ТЕТРАДЬ
- •Задача 1
- •Справочный материал
- •Решение задачи
- •Задача 2
- •Справочный материал
- •Решение задачи
- •Задача 3
- •Справочный материал
- •Решение задачи
- •Задача 4
- •Справочный материал
- •Решение задачи
- •Задача 5
- •Справочный материал
- •Решение задачи
- •Справочный материал
- •Решение задачи
- •Задача 9.1
- •Задача 9.2
- •Справочный материал
- •Решение задачи 9.1
- •Решение задачи 9.2
- •Задача 10
- •Справочный материал
- •Решение задачи 10
- •Задача 11
- •Справочный материал
- •Задача 12.1
- •Задача 12.2
- •Задача 13.1
- •Задача 13.2
- •Справочный материал
- •Наибольшее и наименьшее значения функции двух переменных
- •Условный экстремум функции двух переменных
- •Решение задачи 12.1
- •Решение задачи 12.2
- •Решение задачи 13.1
- •Решение задачи 13.2
- •Приложение
- •Таблица производных основных элементарных функций
- •Правила дифференцирования
- •Формулы Крамера
- •Нормальное уравнение прямой
- •Расстояние от точки до прямой
Справочный материал
Наибольшее и наименьшее значения функции двух переменных
Непрерывная функция z = f (x, y), заданная на ограниченном и
замкнутом множестве D принимает на этом множестве наибольшее и наименьшее значения.
Наибольшее и наименьшее значения могут достигаться в точках экстремума и на границе области, поэтому для их отыскания поступают следующим образом:
определяют стационарные точки функции и вычисляют значения функции в тех стационарных точках, которые содержатся внутри заданного множества;
вычисленные значения функции сравнивают между собой и со значениями функции на границе области. Среди них находят наибольшее и наименьшее.
Условный экстремум функции двух переменных
Если ставится задача найти экстремум функции двух переменных f (x, y) при условии ϕ(x, y)= 0 (условный экстремум), то определяют функцию Лагранжа, которая имеет вид:
L(x, y, λ)= f (x, y)+λϕ(x, y).
Тогда стационарные точки, точки в которых может быть условный экстремум, определяются из системы:
|
∂L = 0 |
|
|
∂x |
|
|
|
|
|
∂L |
= 0 . |
|
∂y |
|
|
|
|
ϕ(x, y)= 0
Если M0 (x0 , y0 ) – стационарная точка, соответствующая значению λ0 (множителю Лагранжа), то функция f (x, y) имеет в точке M0 условный экстремум, если определитель
22
|
0 |
ϕ′x (M 0 ) |
ϕ′y (M 0 ) |
|
|||
= |
ϕ′x (M 0 ) |
∂2 L |
(x0 , y0 ,λ0 ) |
∂2 L |
(x0 , y0 ,λ0 ) |
≠ 0 . |
|
∂x2 |
∂x∂y |
||||||
|
|
|
|
|
|||
|
ϕ′y (M 0 ) |
∂2 L |
(x0 , y0 ,λ0 ) |
∂2 L |
(x0 , y0 ,λ0 ) |
|
|
∂x∂y |
∂y2 |
||||||
|
|
|
|
|
|||
|
|
Функция |
f (x, y) имеет в точке |
M0 условный минимум, если |
|||||||
|
|
< 0 и условный максимум, если |
> 0 . |
|
|
|
|
||||
ЗАМЕЧАНИЕ |
|
|
|
|
|
|
|
||||
|
|
|
|
Если определитель = 0 , то экстремум может быть, а может |
|||||||
|
|
|
|
и не быть. |
|
|
|
|
|
|
|
|
|
|
|
|
Решение задачи 12.1 |
|
|
||||
|
|
Стационарные точки |
функции |
определяются |
из |
системы: |
|||||
∂z |
|
|
|
|
|
|
|
||||
|
|
|
= 2x − y |
−1 = 0 |
|
x =1 |
|
|
|
||
∂x |
|
. Стационарная точка |
|||||||||
|
∂z |
|
. Решение системы |
|
|||||||
|
|
= 2 y − x |
−1 = 0 |
|
y |
=1 |
|
|
|
||
|
|
|
|
|
|
||||||
|
∂y |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
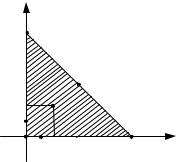
M1(1; 1) находится внутри заданной области (рис.1). Значение |
|||||||||||
функции в этой точке равно z(M1)= −1 . |
|
|
|
|
|||||||
|
|
Граница области задается уравнениями: |
|
|
|
|
|||||
|
|
1. x = 0, |
0 ≤ y ≤ 3 . |
На этой |
части |
границы |
z = y2 − y – |
||||
функция одной переменной. Так как |
z′ = 2y −1 = 0 |
при |
y = 0,5 , то |
||||||||
наименьшее и наибольшее значения функции могут быть в точке |
|||
M 2 (0; 0,5), |
а также в |
граничных |
точках M3(0; 0) и M 4 (0; 3). |
Вычислим |
значения |
во всех |
этих точках: z(M2 )= −0,25 , |
z(M3 )= 0, z(M4 )= 6 . |
|
|
|
23
y |
|
3 |
M 4 |
|
|
|
M7 |
|
|
1 |
M1 |
|
|
|
|
|
|
||
M5 |
|
M6 |
|
|
M3 |
M2 1 |
x |
||
3 |
||||
|
|
Рис. 1. |
|
|
2. y = 0, 0 ≤ x ≤3 . |
На этой части границы z = x2 − x . Так как |
|||
z′ = 2x −1 = 0 при |
x = 0,5 , то наименьшее и наибольшее значения |
|||||
функции могут быть в точке M5 (0,5; 0), а также в граничных точках |
||||||
M3(0; 0) |
и M6 (3; 0). Вычислим |
значения во |
всех этих |
точках: |
||
z(M5 )= −0,25 , z(M6 )= 6 . |
|
|
|
|
||
3. |
y = 3 − x, |
0 ≤ x ≤ 3 . |
На |
этой |
части |
границы |
z = 2x2 +(3 − x)2 −3x −3 . Так как |
z′ = 4x −2(3 − x)−3 = 6x −9 = 0 , |
|||||
при x =1,5 , то наибольшее и наименьшее значения могут быть в
точках M7 (1,5;1,5) и в граничных |
точках M 4 (0; 3) |
и |
M6 (3; 0). |
||||
Вычислим z(M7 )= −0,75 . |
|
|
|
|
|
|
|
Следовательно, наибольшее значение функции равно |
zнаиб = 6 |
||||||
в точках M 4 (0; 3) и M6 (3; 0), |
а |
наименьшее |
zнаим = −1 в |
||||
стационарной точке M1(1;1). |
|
|
|
|
|
|
|
Решение задачи 12.2 |
|
|
|||||
Вычислим частные производные |
|
|
|
|
|||
|
∂z |
|
= y |
= 0 |
|
|
|
|
|
|
|
|
|||
∂x |
|
|
|||||
|
|
|
|
. |
|
|
|
∂z |
|
= x |
|
|
|||
|
|
|
= 0 |
|
|
||
|
|
|
|
||||
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24
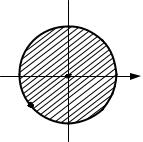
Стационарная точка M1(0; 0) принадлежит области x2 + y2 ≤1
(рис.2). Значение функции в этой точке z(M1 )= 0 . y
M5
 M 2
M 2
M1
x
M3  M4
M4
Рис. 2.
Исследование функции на границе можно проводить двумя способами.
1.Границей области является окружность, заданная уравнением
x2 + y2 =1. Запишем это уравнение в параметрическом виде:
|
|
|
|
|
|
|
x = cost |
, 0 ≤ t ≤ 2π. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
= sin t |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||
Подставляя значения |
x(t) и |
y(t) в функцию |
z = x y , |
получим |
|||||||||||||
функцию z = cost sin t = |
1 sin 2t |
одной переменной |
|
t , заданную на |
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
промежутке |
|
[0; 2π]. Наибольшее и наименьшее |
значения |
эта |
|||||||||||||
функция может принимать на концах промежутка при t = 0 , |
t = 2π, а |
||||||||||||||||
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
также в точках, в которых z (t)= 0 . |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
′ |
1 |
|
|
|
′ |
|
|
|
π |
|
πk |
Вычислим |
|
|
|
|
|
|
при t = 4 + 2 , |
||||||||||
|
z (t)= 2 cos 2t 2 = cos 2t . z (t)= 0 |
||||||||||||||||
где k - целое число. |
|
|
|
|
|
|
|
|
|
|
|||||||
Внутри |
промежутка |
[0; 2π] |
содержатся только |
точки |
|
t |
= π , |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 = |
3π |
, t3 |
= |
|
5π |
|
и t4 = |
7π |
. |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||
25
Вычислим значения функции z = 12 sin 2t во всех этих точках.
z(t1 )= 12 sin π2 = 0,5 , z(t2 )= 12 sin 32π = −0,5 , z(t3 )= 12 sin 52π = 0,5 , z(t4 )= 12 sin 72π = −0,5 .
Вычислим значение функции z = 1 sin 2t на концах промежутка. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
z(0)= 0 , z(2π)= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Следовательно, |
наибольшее |
значение |
функции |
равно |
0,5 , |
||||||||||||||||||||||||||||||||||||||||||
которое достигается в точке |
|
|
(cos |
|
π |
, sin |
|
π |
), |
|
|
|
1 |
|
, |
1 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
и в точке |
||||||||||||||||||||||||||||||||
|
4 |
|
4 |
|
2 |
|
2 |
||||||||||||||||||||||||||||||||||||||||
(cos |
|
|
|
|
|
), или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5π |
, sin |
5π |
|
− |
|
|
1 |
|
, − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Наименьшее |
значение |
|
|
|
|
функции |
|
равно |
|
|
|
−0,5 , |
которое |
||||||||||||||||||||||||||||||||||
достигается |
|
в точке |
|
|
(cos |
3π |
|
, sin |
|
3π |
) |
, |
|
или |
|
− |
1 |
|
, |
|
1 |
|
|
и |
в |
точке |
|||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
(cos |
|
|
|
|
|
), или |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|||||||||||
7π |
, sin |
7 |
π |
|
1 |
|
, |
− |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
4 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2. Исследование функции на границе области – задача условного |
|||||||||||||||||||||||||||||||||||||||||||||||
экстремума |
|
|
функции |
|
|
|
z = xy |
|
|
|
|
при |
|
условии |
x2 + y2 =1 . |
Функция |
|||||||||||||||||||||||||||||||
Лагранжа имеет вид |
|
|
L(x, y, λ)= xy +λ(x2 + y2 −1). |
Стационарные |
|||||||||||||||||||||||||||||||||||||||||||
точки определяются из системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂L |
|
= y |
+2λx = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂L |
= x |
+2λy = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ y |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычитая |
|
|
из |
|
|
первого |
|
|
|
|
уравнения |
|
второе, |
|
получим: |
||||||||||||||||||||||||||||||||
(y − x)−2λ(y − x)= 0 , (y − x)(1−2λ)= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
26
