
pz_grafy_
.pdfМинистерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра математики
ОСНОВЫ ТЕОРИИ ГРАФОВ
Материалы практических занятий Дискретная математика
Санкт-Петербург
2013 г.
1
Оглавление. |
|
.2.1. Виды графов, способы их задания, операции над графами |
3 |
2.1.1. Операции, производимые над графами |
3 |
2.1.2. Изоморфизм графов |
6 |
2.2. Матрицы, связанные с графом |
8 |
2.3. Маршруты, цепи, циклы . Связные графы |
14 |
2.4. Метрические характеристики графа. Взвешенные графы |
15 |
2.6. Нахождение кратчайших маршрутов |
16 |
2.6.1. Алгоритм Форда–Беллмана |
16 |
2.6.2. Алгоритм Дейкстры |
20 |
2.7 .Эйлеровы циклы и графы |
27 |
2.8. Гамильтоновы циклы и графы . Решение задачи |
|
коммивояжера методом ветвей и границ |
28 |
2.9. Упорядоченные и бинарные деревья |
36 |
2.10. Остов минимального веса. Алгоритм Краскала. |
37 |
2.11. Фундаментальные циклы и фундаментальные разрезы |
38 |
2.12. Плоские и планарные графы. Критерии планарности графа. |
42 |
2
Практические занятия
2.Основы теории графов
2.1.Виды графов, способы их задания, операции над графами
2.1.1. Операции над графами
Напомним, что объединением графов |
G1 (V1 , E1 ) |
и G2 (V2 , E2 ) |
||||||||||
называется граф G G1 G2 |
(V , E) , где V V1 V2 , |
E E1 E2 ; пе- |
||||||||||
ресечением графов G1 и G2 |
называется граф G G1 G2 (V , E) , |
где |
||||||||||
V V1 V2 , E E1 E2 ; |
произведением |
двух графов |
G1 |
(V1 , E1 ) и |
||||||||
G2 (V2 , E2 ) называется |
граф G G1 G2 |
(V , E) , где |
V V1 V2 |
– |
||||||||
декартово |
произведение |
множеств |
вершин |
исходных |
графов |
и дуга |
||||||
((u1 , v1 ),(u2 , v2 )) E тогда и только тогда, когда u1 |
u2 |
и |
(v1 , v2 ) E2 |
|||||||||
или v1 v2 |
и (u1 ,u2 ) E1 ; кольцевой суммой графов G1 |
и G2 называется |
||||||||||
граф |
G G1 G2 (V , E) , |
|
где |
|
|
|
V V1 V2 , |
|||||
E E1 E2 (E1 \ E2 ) (E2 \ E1 ) . |
|
|
|
|
|
|
|
|
|
|||
Задача |
2.1. Заданы |
графы |
G1 (V1 , E1 ) , |
где |
V1 {1,2,3,4}, |
|||||||
E1 {{1,2},(1,3),{2,2},(2,4), {3,4}} |
и G2 |
(V2 , E2 ) , |
где |
V2 |
{1,2,3} , |
|||||||
E2 {{1,1}, (1,2), (1,3),{2,3}}. |
Построить |
графы |
G1 |
G2 |
, |
G1 G2 , |
||||||
G1 G2 , G1 G2 . |
|
|
|
|
|
|
|
|
|
|
|
|
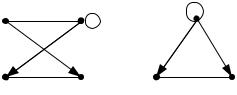
Графы изображены на рис. 2.1
1
G1 :
4
2 |
1 |
|
|
G2 : |
|
3 |
3 |
2 |
Рис. 2.1
3

1) Построим граф G (V , E) , являющийся объединением графов
G1 (V1 , E1 ) |
и G2 (V2 , E2 ) . В этом случае V V1 V2 {1,2,3,4}, |
E E1 E2 |
({1,1},(2,2},{1,2},(1,3),{2,3}, (2,4), {3,4}} |
На рис. 2.2 представлен граф G1 G2
|
1 |
2 |
G3 : |
4 |
3 |
|
|
G1 G2 |
Рис. 2.2 2) Найдем граф, являющийся пересечением заданных графов.
В этом случае V V1 V2 {1,2,3}, E E1 E2 {(1,2), (1,3)}, где (1,2) –
дуга. На рис. 2.3 представлен граф G1 G2 .
1
G4 |
: |
3 |
2 |
|
|
G1 G2
Рис. 2.3
3) Найдем произведение G G1 G2 двух заданных графов. Для этого прежде всего построим V V1 V2 прямое произведение множеств вер-
шин первого и второго графов
V {(1,1), (1,2),(1,3),(2,1),(2,2), (2,3),(3,1),(3,2),(3,3),(4,1), (4,2),(4,3)} и
найдем все дуги прямого произведения графов, учитывая, что дуга
4
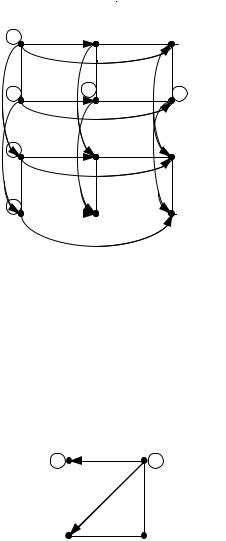
((u1 , v1 ),(u2 , v2 )) E тогда и только тогда, когда u1 u2 и (v1 , v2 ) E2 или v1 v2 и (u1 ,u2 ) E1 . В результате получим граф, изображенный на рис.2.4
(1,1) |
(1,2) |
(1,3) |
|
||
(2,1) |
(2,2) |
(2,3) |
(3,1) |
(3,2) |
(3,3) |
|
|
G5 : |
|
|
|
|
|
|
|
|
|
(4,1) |
(4,2) |
(4,3) |
||
|
|
Рис.2.4 |
|
|
4) Построим кольцевую сумму G G1 G2 |
(V , E) графов G1 и G2 , где |
|||
V V1 V2 , E E1 E2 |
(E1 \ E2 ) (E2 \ E1 ) . В данном случае |
|||
V V1 V2 {1,2,3,4},
EE1 E2 (E1 \ E2 ) (E2 \ E1 )
{({1,1}, (2,2},(2,1),{2,3}, (2,4), {3,4}}
Граф G6 G1 G2 изображен на рис. 2.5
|
1 |
2 |
G6 : |
4 |
3 |
|
|
Рис. 2.5 |
|
|
5 |
|
2.1.2. Изоморфизм графов |
|
|||
Графы, которые получаются один из другого переименованием вершин, |
|||||
не различаются. Два графа G1 (V1 , E1 ) |
и G2 (V2 , E2 ) называются изо- |
||||
морфными, |
если существует биекция |
f :V1 V2 такая, что для любых |
|||
двух вершин u и v графа G1 |
их образы |
f (u) и f (v) |
смежны в G2 тогда и |
||
только тогда, когда u и v смежны в G1 . Для изоморфных графов использу- |
|||||
ется обозначение G1 G2 . |
|
|
|
|
|
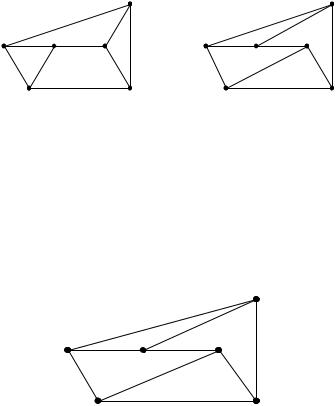
Задача 2.2 Являются ли изоморфными графы G1 |
и G2 , изображенные |
||||
на рис. 2.6 |
|
|
|
|
|
|
|
4 |
|
|
|
|
6 |
|
|
|
|
2 |
5 |
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
G1 |
|
|
G2 |
|
|
|
Рис.2.6 |
|
|
|
Решение. Графы G1 и G2 |
являются изоморфными. Это легко устано- |
||||
вить, если перенумеровать вершины графа G2 так, как это показано на |
|||||
рис.2.7. Тогда при взаимно однозначном отображении |
f : k k' |
||||
( k 1,2,3,4,5,6 ) две вершины k ' и j' |
смежны тогда и только тогда, когда |
||||
смежны k и |
j |
|
|
|
|
|
|
|
|
1' |
|
|
2' |
|
|
5' |
|
|
|
|
|
|
|
|
|
6' |
|
|
|
|
4' |
|
|
|
3' |
|
|
|
|
|
|
|
|
6 |
|
|
|
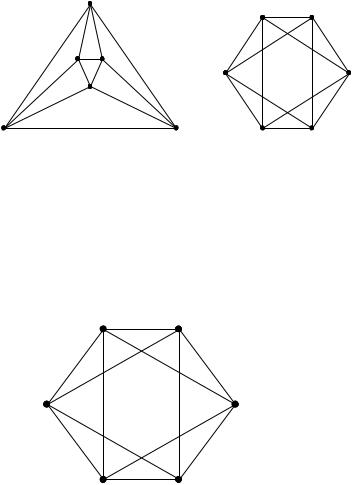
Рис. 2.7
Задача 2.3. Являются ли изоморфными графы G1 и G2 , изображенные на рис. 2.8
3
4 |
5 |
6 |
1 |
G1 |
|
2 |
G2 |
|
Рис. 2.8
Решение. Графы G1 и G2 являются изоморфными. Это можно устано-
вить, если перенумеровать вершины графа G2 так, как это показано на рис.2.9. Тогда при взаимно однозначном отображении f : k k'
( k 1,2,3,4,5,6 ) две вершины k ' и j' смежны тогда и только тогда, когда смежны k и j
6' 5'
2' |
4' |
1' G2 3'
Рис. 2.9
7
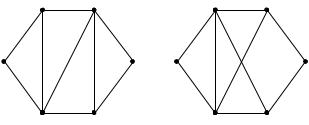
Задача 2.4. Установить, что графы G1 и G2 , изображенные на рис. 2.10, не изоморфны.
5 |
4 |
|
|
5' |
4' |
|
|
|
|
|
|
6 |
|
|
6' |
|
3' |
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
1' |
|
2' |
|
|
|
G2 |
||
|
G1 |
|
|
|
|
|
|
|
|
|
Рис. 2.10
2.2. Матрицы, связанные с графом
Напомним основные определения таких матриц.
Матрицей смежности A(G) графа G называется квадратная матрица
An n (aij ) порядка n с матричными элементами
|
1, если вершины i и j смежны, |
||
aij |
|
0, |
в противном случае |
|
|
||
Матрица, каждый элемент которой равен 0 или 1, называется бинарной. Матрица A(G) является симметрической матрицей с нулями на главной
диагонали. Число единиц в каждой строке равно степени соответствующей вершины. Матрица смежности для мультиграфа определяется как квадрат-
ная матрица с матричными элементами aij k , где k – кратность ребра
{vi , v j } . Матрица смежности для мультиграфа является симметричной мат-
рицей из неотрицательных целых чисел, на главной диагонали которой находятся нули. Аналогично определяется матрица смежности для псевдографа, который содержит петли, т.е. ребра, начинающиеся и кончающиеся в одной и той же вершине. В этом случае на главной диагонали появляются соответствующие петлям положительные числа.
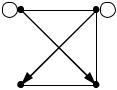
Матрицей смежности для орграфа является квадратная матрица An n (aij ) порядка n с матричными элементами
8
|
1, если вершина i начало ребра,конец которогов вершине j |
||||||
aij |
|
|
|
|
|
|
|
|
0, |
|
|
|
в |
противном случае |
|
Матрица смежности для орграфа – несимметричная матрица из нулей и |
|||||||
единиц, на главной диагонали которой находятся нули. |
|||||||
Матрицей инцидентности (n, m) –неорграфа G (V , E) называется бинар- |
|||||||
ная матрица размерности n m с матричными элементами |
|||||||
|
1, если вершина k и ребро e j |
инцидентны |
|
||||
I kj |
|
|
|
|
|
|
. |
|
0 |
в противном случае |
|
||||
Для ориентированных графов матрица инцидентности B (bij ) , где |
|||||||
i 1,2,..., n , j 1,2,..., m ,: |
|
|
|
|
|
||
I kj |
1, если вершина k является началом дуги e j |
, |
|
||||
I kj |
1, если вершина k является концом дуги e j , |
|
|||||
I kj |
0 , если вершина k и дуга e j |
не инцидентны или если дуга e j являет- |
|||||
ся петлей. |
|
|
|
|
|
|
|
|
Поскольку каждая дуга инцидентна двум различным вершинам, за ис- |
||||||
ключением того случая, когда дуга образует петлю, то каждый столбец мат- |
|||||||
рицы инцидентности либо содержит один элемент, равный 1, и один – рав- |
|||||||
ный –1, либо все элементы столбца равны нулю. |
|
|
|||||
|
Задача 2.5. Для графа G , приведенного на рис.2.11, найти матрицу |
||||||
смежности AG и |
матрицу инцидентности I G |
|
|
||||
|
|
1 |
e1 |
2 |
e7 |
|
|
|
|
e6 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
e4 |
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
e5 |
|
|
|
|
|
|
|
4 |
e3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.11 |
|
|
|
||
Решение. Матрица смежности и матрица инцидентности имеют вид |
|||||||
|
|
|
9 |
|
|
|
|
|
1 |
1 |
1 |
0 |
||
|
|
|
|
|
|
|
AG |
|
1 |
1 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
||||
|
|
|
|
e1 e2 |
e3 e4 |
e5 |
e6 e7 |
|
||||
|
|
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
||
IG |
|
2 |
|
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
||||||||
|
|
3 |
|
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
0 |
0 |
1 |
0 |
1 0 |
0 |
|
||
|
|
4 |
|
|||||||||
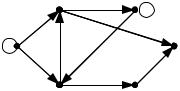
Задача 2.6. Для графа G , приведенного на рис.2.12, |
найти матрицу |
||||
смежности AG и |
матрицу инцидентности I G |
|
|||
|
|
1 |
e1 |
2 e3 |
|
|
|
e9 |
|
|
|
|
|
|
e2 |
|
|
|
e10 |
e8 |
|
|
|
|
e4 |
3 |
|
||
|
|
6 |
|
||
|
|
e7 |
|
e5 |
|
|
|
|
|
|
|
|
|
5 |
e6 |
4 |
|
|
|
|
Рис. 2.12 |
|
|
Решение. Матрица смежности и матрица инцидентности имеют вид |
|||||
|
|
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
0 |
1 |
1 |
0 |
0 |
0 |
||||
|
|
2 |
|
0 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
3 |
|
|
|||||||
AG |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
||
4 |
|
|
|||||||||
|
|
|
0 |
1 |
0 |
0 |
|
||||
|
|
|
0 |
0 |
|||||||
|
|
5 |
|
1 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|||||||
|
|
6 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|||||||
10
