pz_grafy_

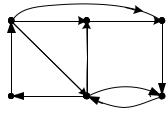
Введем обозначения S {vi } , T V \ S .

2) Для вершин vk T , связанных дугами с вершинами из множества S , метки пересчитываются в соответствии с правилом

m(vk ) min{m(vk ), m(vi ) wik }

vi S

3) Из меток, которые были пересчитаны, выбрать вершину u с наименьшей меткой и образовать множества S' S {u} , T ' V \ S' .

Если S' S , то m(u) – длина кратчайшего пути из вершины vi в вершину u (при этом если m(u) , то не существует пути из вершины vi в верши-

ну u ). Если S' S , то S : S' , T : T ' и перейти к п.2.

В результате получится кратчайший путь от вершины vi до всех вершин графа. При этом если кратчайший путь из вершины vi до вершины v j про-

ходит через вершину vk , то пути от вершины vi до вершины vk и от вер-

шины vk до вершины v j являются минимальными.

Решение задачи таким способом представляют в виде таблицы, содержащей метки вершин.

Задача 2.12 Для взвешенного графа G (V , E) , изображенного на рис.

2.18, с матрицей весов W найти наименьшие взвешенные расстояния от вершины 1 до всех остальных вершин с помощью алгоритма Дейкстры. Указать минимальный взвешенный маршрут от вершины до вершины 5.

Решение. Матрица весов заданного графа имеет вид

21

Составим таблицу, в которой окончательные метки заключены в скобки. Окончательные метки выделим жирным шрифтом.

Отметим, что в результате пересчета меток в каждой строке таблицы появляется одна новая окончательная метка, которая равна соответствующему минимальному взвешенному расстоянию.

Таблица 2.2

Отсюда окончательные метки для вершин 1,2,3,4,5,6 соответственно (0), (1), (4), (3), (6), (5). Эти метки определяют кратчайшие взвешенные расстояния от вершины 1 до вершин 1,2,3,4,5,6 соответственно.

Кратчайший путь между вершинами 1 и 5 найдем, если перемещаться от вершины 5 по вершинам с окончательными метками в направлении против стрелок. На первом шаге выбираем вершину, смежную с 5 и такую, что ее метка плюс расстояние до 5 дает метку вершины 5. Аналогично осуществляются второй и последующий шаги. Таким способом получим последова-

тельность вершин 5 6 3 4 2 1. Отсюда кратчайший путь от вершины 1 до вершины 5 определяется входящими в него вершинами и имеет вид: 1 2 4 3 6 5 .

..

22

2.5.2. Нахождение кратчайших маршрутов в бесконтурном графе

Пусть граф G (V , E) является бесконтурным взвешенным графом с мат-

рицей весов W (wij ) . Напомним, что бесконтурным называется граф, не

содержащий контуров, т.е. в таком графе не существует путей, начинающихся и кончающихся в одной вершине. Кратчайший маршрут в таком графе можно найти с помощью аналога алгоритма Форда-Беллмана, в котором учтена бесконтурность графа.

В конечном бесконтурном графе вершины можно перенумеровать так, что каждая дуга будет иметь вид (vi , v j ) , где i j . Действительно, в таком графе существует вершина, в которую не заходит ни одна дуга. Обозначим эту вершину v1 и рассмотрим граф G1 , полученный из G удалением вер-

шины v1 . Граф G1 также является бесконтурным, поэтому в нем также су-

ществует вершина v2 , в которую не заходит ни одна дуга. Продолжая этот процесс, получим такую нумерацию вершин, что каждая дуга будет иметь вид (vi , v j ) , где i j . При такой нумерации все элементы матрицы весов,

стоящие под главной диагональю, равны .

23

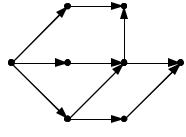
Задача 2.13. Для бесконтурного взвешенного графа, изображенного на рис. 2.18, найти минимальные взвешенные расстояния до всех остальных вершин.

Рис. 2.18

Матрица весов для заданного графа имеет вид

Строка D(1) представляет собой первую строку матрицы весов: D(1) (0,1, ,2, , ,1, ) . Элементами второй строки являются

24

d1(2) d1(1) 0

d2(2) min{d2(1) , d1(1) w12} min{1,0 1} 1,

Для нахождения последующих элементов строки для каждого j и s вначале построим множества вида

C (js 1) {d1(s) w1 j , d2(s) w2 j ,..., dk(s) wkj ,..., d (js)1, j wj 1, j }, в которых по-

ка не выполняется условие (vk , v j ) E . Подчеркнем те элементы этого

25

Минимальные взвешенные расстояния от вершины 1 до остальных вершин графа равны соответственно w (1,1) 0 , w (1,2) 1, w (1,3) 1,

w (1,4) 2 , w (1,5) 3 , w (1,6) 3 , w (1,7) 1, w (1,8) 2 . Соот-

ветствующие минимальные взвешенные маршруты: 1 2 , 1 2 3 ,

1 4 , 1 4 5 , 1 2 3 6 ,1 7 , 1 7 8 .

26

2.6. Эйлеровы циклы и графы.

Путь (цепь) называется эйлеровым, если этот путь содержит все ребра графа только по одному разу. Эйлеровым циклом называется эйлеров путь, являющийся циклом. Мультиграф называется эйлеровым, если он содержит эйлеров цикл. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечетной степени. Связный неориентированный мультиграф является эйлеровым тогда и только тогда, когда степень каждой из его вершин является четным числом.

Алгоритм Флёри построения эйлерова цикла в эйлеровом мультиграфе. 1). Выбрать произвольную вершину v .

2)Выбрать произвольное ребро, инцидентное v , и присвоить ему номер 1. Вычеркнуть это ребро. Перейти в вершину u .

3)Выбрать ребро, инцидентное вершине u , присвоить ему номер 2 и вы-

черкнуть его. При этом, находясь в вершине u , не выбирать ребро (u, v) ,

если есть такая возможность, и не выбирать ребро, после удаления которого граф, образованный невычеркнутыми ребрами, распадается на две компоненты связности, каждая из которых имеет хотя бы по одному ребру (т.е. не выбирать мост).

4) Продолжая этот процесс, получим эйлеров цикл, после того, как в графе будут занумерованы все ребра.

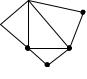
Задача 2.14. Найти эйлеровы циклы для графа изображенного на рис.

2.19

2 3

1

Рис.2.19

Заданный граф имеет два эйлеровых цикла С=(1,2,3,4,5,6,4,2,6,1) и С’=(1,2,6,5,4,3,2,4,6,1). Здесь цикл С’ отличается от цикла С тем, что порядок обхода ребер в подцикле (2,3,4,5,6,4,2) меняется на противоположный. На основании теоремы Коцига таким образом можно получить все эйлеровы циклы из данного цикла

27

2.7. Гамильтоновы графы и циклы. Решение задачи коммивояжера методом ветвей и границ

Простая цепь называется гамильтоновой, если она содержит все вершины данного графа.

Простой цикл называется гамильтоновым, если он содержит все вершины данного графа.

Граф называется гамильтоновым, если в нем имеется простой цикл, содержащий каждую вершину графа.

.

Бродячий торговец должен посетить район, содержащий n городов, расстояния между которыми известны. Требуется найти кратчайший маршрут, проходящий все пункты по одному разу и возвращающийся в исходный город.

Математически задача сводится к нахождению гамильтонова цикла минимального веса. Пусть W (wij ) – матрица весов графа G (V , E) , где

V {1,2,..., n}. Элементы wij 0 . Найдем нижнюю оценку весов гамильто-

новых циклов. Для каждой строки матрицы весов найдем минимальные эле-

Обозначим через (v1, v2 ,..., vk ){u1,u2 ,...,ut } множество гамильтоновых циклов, в которых первые k вершин v1 , v2 ,..., vk , а k 1–я вершина vk 1 не принадлежит множеству {u1,u2 ,...,ut }.

28

Представим множество гамильтоновых циклов в виде объединения множеств (1, k1 ) A и (1){k1}.Первое из этих множеств содержит гамильтоновы циклы с двумя первыми вершинами 1 и k1 . Второе множество содержит гамильтоновы циклы, у которых первая вершина 1, а вторая вершина имеет номер, отличный от k1 .

Рассмотрим вначале множество (1, k1 ) A . Отождествим в графе G вершины

1 и k1 . Обозначим новую вершину через x . Тогда получим граф G' с мно-

Для графа G' найдем нижнюю оценку h' весов гамильтоновых циклов подобно тому, как были найдены оценки h . Тогда нижняя оценка h1 весов га-

мильтоновых циклов множества (1, k1 ) A равна h1 h h' .

Рассмотрим теперь множество (1){k1}. В этом случае в матрице весов W

элемент w1k1 заменяется на . По полученной матрице весов находится нижняя оценка h'' весов гамильтоновых циклов графа с матрицей весов W ''. Тогда нижняя оценка h2 весов гамильтоновых циклов множества

(1){k1}равна h h'' .

Затем каждая из подзадач разбивается на свои подзадачи и производится оценка весов гамильтоновых циклов до тех пор, пока не отыщется самая низкая из оценок, которая является весом некоторого гамильтонова цикла.

При решении этой задачи рекомендуется вести поиск в глубину, при котором на каждом следующем шаге выбирается та подзадача, которая имеет меньшую нижнюю оценку.

29

Задача 2.15. Граф G (V , E) , где V {1,2,3,4},

E {(1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,3), (2,4), (2,5), (3,1), (3,2), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,5), (4,6), (5,2), (5,3), (5,4), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5)

заданный структурой смежности

Найти гамильтонов цикл минимального веса. Решение.

Множество всех гамильтоновых циклов в данном случае имеет вид , представленный таблицей 2.3

Таблица 2.3

30