7.18. Дисперсия дискретной случайной величины

Итак, мы получили меру отклонения по результатам n опытов: среднее арифметическое квадратов отклонений

=

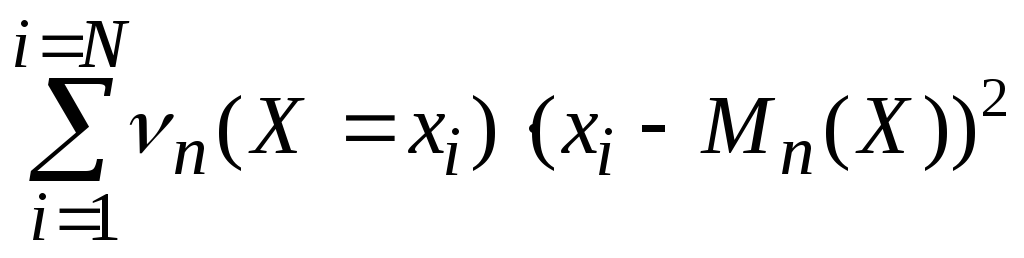
Но полученное значение может отличаться при повторениях серий из n опытов, а желательно иметь стабильное значение величины, описывающей разброс значений случайной величины.

Искомая стабильная величина получается при неограниченном увеличении числа опытов. Название у неё будет: дисперсия – рассеяние.

При возрастании количества опытов n частоты отдельных значений стремятся к их вероятностям, т.е. к значениям закона распределения.

,

среднее арифметическое – к математическому ожиданию

Соответственно, выражение для среднего арифметического квадратов отклонений изменится так

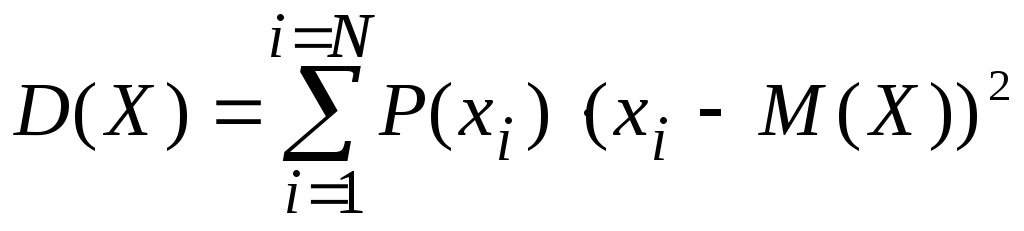
В этом выражении вместо частот стоят значения закона распределения, а возле обозначения дисперсии D опущена буква n.

N (эн большое) – это, по-прежнему, количество возможных значений.

–значения закона распределения дискретной случайной величины (вероятности отдельных возможных значений x_i случайной величины).

В теории вероятности дисперсия дискретной случайной величины вычисляется без проведения каких-либо опытов, если известны значения закона распределения.

Таким образом, дисперсия дискретной случайной величины вычисляется как средний квадрат отклонения значений случайной величины от математического ожидания.

На практике столь же часто пользуются и другой мерой рассеяния, которую находят как квадратный корень из дисперсии:

.

Она носит название среднеквадратическое отклонение (или стандартное отклонение).

Если единицы измерения случайной величины X обозначить «е.и.», то матожидание измеряется также в «е.и.».

Единица измерения дисперсии – квадрат размерности случайной величины, т.е. «е.и.²», а среднеквадратическое отклонение – снова в «е.и.».

7.19. Дисперсия непрерывной случайной величины

Для дискретной случайной величины дисперсия вычисляется по уже известной нам формуле:

.

Для непрерывной случайной величины выражение аналогично, но с использованием интеграла. Запишем его без вывода

.

Интеграл стоит вместо суммы.

Вместо вероятности отдельного значения P(x_i) стоит p(x)  dx , которое по смыслу является вероятностью попадания в бесконечно малый интервал dx.

У равномерно распределённой случайной величины, т.е. у которой плотность распределения отлична от нуля только на отрезке от a до b и имеет в его пределах постоянное значение, дисперсия такова

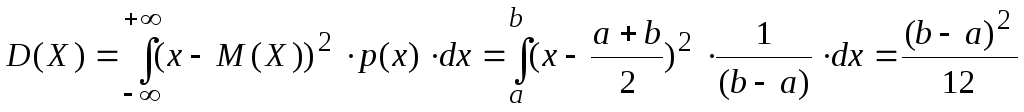
У нормально распределённой случайной величины или у нормального распределения дисперсия равна параметру :

=

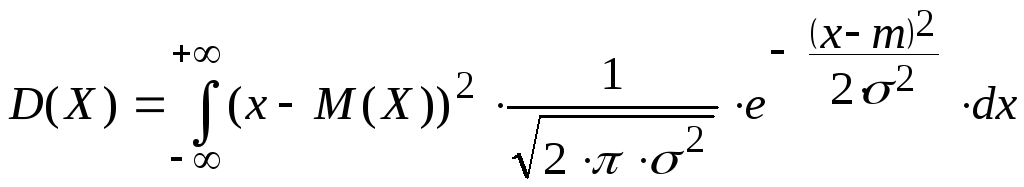То, что у нормального распределения формула в явном виде содержит математическое ожидание и дисперсию – это очень удобно.

Почему удобно, сейчас узнаем.

7.20. СИММЕТРИЧНЫЕ ИНТЕРВАЛЫ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Нормальное распределение, как это можно видеть из математической записи, зависит только от двух параметров: математического ожидания и дисперсии.

Существует даже специальное краткое обозначение плотности вероятности нормального распределения, отражающее этот факт:

Изобразим на рисунке плотность вероятности нормальной случайной величины Хс заданными математическим ожиданиемmи дисперсией.

Н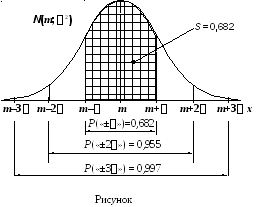а горизонтальной оси отметим точку математического ожидания.

Если дана дисперсия  ², то значит можно вычислить из неё квадратный корень и получить среднеквадратическое отклонение .

Отложим обе стороны от точки математического ожидания расстояния в одну «сигму».

Получим точки m–иm+.

Эта пара точек образует интервал, симметричный относительно плотности нормального распределения.

Вероятность того, что нормальная случайная величина Хпримет значение в пределах интервала отm–доm+равна, как точно вычислили математики, – 0,682.

P(m–Х<m+) = 0,682

Что это за значение 0,682. Это площадь под центральной частью кривой.

А под всей кривой, помним, площадь – единица.

Теперь отложим от математического ожидания уже по две «сигме».

Получим точки m–2иm+2.

Вероятность того, что нормальная случайная величина Хпримет значение в пределах отm–2доm+2, равна – 0,955.

P(m–2Х<m+2) = 0,955

И, наконец, отложим по три «сигмы».

Получим точки m–3иm+3.

Вероятность того, что нормальная случайная величина Хпримет значение в пределах отm–3доm+3, равна – 0,997.

P(m–3Х<m+3) = 0,997

Каждая рассмотренная пара точек образует интервал, симметричный относительно плотности нормального распределения.

0,682; 0,955 и 0,997 – это вероятности попадания в симметричные интервалы, соответствующие однократному, двукратному и трёхкратному отклонениям.

Смыслы интервалов с точки зрения попадания в них случайной величины таковы:

в интервал по однократному отклонению – попадает большинство;

по двукратному – попадает подавляющее большинство;

по трёхкратному – попадают практически все.

Наиболее используемым и поэтому известным является интервал трёхкратного отклонения.

В него в среднем попадают 99,7 % всех значений, т.е. в среднем не попадают только 3 из 1000.

В статистическом обиходе даже имеется так называемое «правило 3-х сигм»:

в интервал плюс минус 3 сигмы от математического ожидания в среднем попадает 99,7 % значений нормальной случайной величины.

Собственного названия рассмотренные интервалы не имеют. Однако в задачах управления качеством выпускаемой продукции эти интервалы именуются интервалами допуска.

Например, автоматическая линия выпускает изделия со средним значением какого-либо показателя (вес изделия, диаметр, концентрация) равным m.

У каждого отдельного изделия этот показатель может быть чуть больше или чуть меньше среднего, но не намного.

Изредка с конвейера сходят изделия с большими отклонениями показателя от среднего значения.

Они должны отбраковываться.

Для отбраковки устанавливается некоторый интервал.

Попадание значения показателя изделия в его пределы означает приёмку этого изделия. Выход же за пределы этого интервала означает недопуск изделия.

Поэтому такой интервал называется интервалом допуска.