1.5. Типы балок

Балка — это стержень или брус, работающий преимущественно на изгиб. Статически определимые балки разделяются на следующие типы (рис. 1.8):

• простые балки — балки на двух опорах по концам;

• консольные — балки на двух опорах со свешивающимися концами или консолями;

• консоли — балки, защемлённые одним концом;

• шарнирно-консольные балки, составленные из двух или нескольких последовательно расположенных балок, концы которых связаны между собой шарнирами.

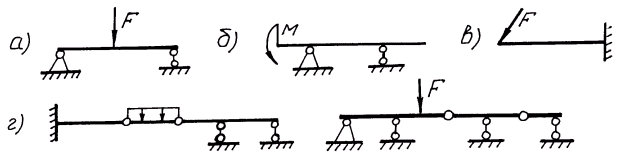
Рис. 1.8. Различные типы балок: а – простая балка; б – консольная балка; в – консоль; г – шарнирно-консольная балка

Расстановка шарниров в многопролётной балке должна быть произведена так, чтобы она была статически определимой и геометрически неизменяемой:

• в каждом пролёте должно быть размещено не более двух шарниров;

• пролёты с двумя шарнирами должны быть размещены не менее чем через пролёт;

• пролёты с одним шарниром могут следовать один за другим, если в системе есть одна неподвижная балка.

Консоль, простая балка и балка с консолями — это геометрически неизменяемые и статически определимые системы.

Длина консоли называется вылетом консоли, а длина простой балки – пролётом.

1.6. Порядок расчёта шарнирно-консольных балок

1. Подсчитывают степень свободы системы.

2. Проводят анализ геометрической неизменяемости системы. Изображают схему взаимодействия элементов шарнирно-консольной балки, то есть поэтажную схему, для чего мысленно разъединяют элементы балки, разделив их на основные или главные, которые могут самостоятельно воспринимать внешнюю нагрузку, и второстепенные или присоединённые, которые не могут работать самостоятельно, а должны опираться на основные балки в соответствии с рисунком 9.

3. Аналитический расчёт шарнирно-консольных балок начинают со второстепенной балки самого верхнего этажа. Построив для верхней балки эпюры изгибающихся моментов и поперечных сил, прикладывают реакцию опоры на нижележащую балку с обратным направлением и рассчитывают её. Последней рассчитывается опорная балка.

Признаки основной и второстепенной частей:

• если разрушается основная часть, то разрушается вся система;

• при разрушении второстепенной части, основная или главная остаётся без изменения.

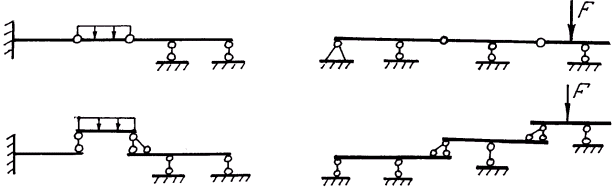
Рис. 1.9. Поэтажные схемы шарнирно-консольных балок

Контрольные вопросы

1. Почему недопустимы системы, близкие к мгновенно изменяемым?

2. Для чего проводится кинематический анализ систем?

3. Как проверить статическую определимость и геометрическую неизменяемость многопролетной статически определимой балки?

2. Расчёт сооружений на подвижную нагрузку

При расчёте сооружения на подвижную нагрузку: движущийся поезд, автомобиль – пользуются линиями влияния (лв).

Линия влияния – это график, показывающий закон изменения того или иного усилия: реакции, момента, поперечной силы – в определённом или фиксированном сечении сооружения при перемещении по его длине груза F=1.

Ордината линии влияния показывает величину усилия, для которого построена ЛВ, когда груз F=1 стоит над этой ординатой на сооружении.

Ординаты линий влияния R и Q безразмерны, а линии влияния М выражаются в метрах.

Сравнение линий влияния и эпюр какого-либо усилия J приведены в табл. 2.1.

Таблица 2.1

Сравнение линии влияния и эпюр

Вид графика	Положение груза	Положение сечения	Вид нагрузки
Эпюра	Постоянное	Переменное	Любая
Линия влияния	Переменное	Постоянное	Единичная