НГиИГ / 32.Пересечение прямой линии с поверхностью многогранника

32.Пересечение прямой линии с поверхностью многогранника.

Прямая с многогранной поверхностью может не иметь точек пересечения, может касаться в одной точке и может пересекать многогранную поверхность в нескольких точках, причем четное количество раз. Если многогранник выпуклый, то существует только две точки пересечения прямой с многогранной поверхностью. Рассмотрим общий алгоритм решения этой задачи на следующем примере (рис. 6.7). Дана трехгранная призма и прямая а — общего положения. Требуется найти точки пересечения M и N.

Алгоритм построения точек пересечения прямой с многогранной поверхностью:

1. Заключаем прямую a во вспомогательную плоскость : a  .

2. Плоскость  пересекает многогранник по ломаной KLP.

3. Ломаная KLP пересекается с прямой a в точках N и M. Точки N и M — искомые точки пересечения прямой a с многогранником.

Выбор положения вспомогательной плоскости  осуществляется, исходя из точности и простоты построений. Теперь рассмотрим на чертеже пример построения точек пересечения прямой а общего положения с трехгранной призмой ABCA'B'C' (рис. 6.8). Для этого через прямую а проведем фронтально проецирующую плоскость : а  .

Алгоритм построения:

1. Через a₂ вводим вспомогающую проецирующую плоскость 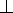  П₂, a₂ = _

2. Отмечаем проекции K₂, P₂, L₂ точек K, P,L, где K 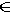 AA', P  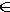BB', L  CC'.

3. Из условия принадлежности определяем их первые проекции K₁, P₁,L₁.

4. При пересечении a₁ с треугольникомK₁P₁L₁ получаем горизонтальные проекции N₁ и M₁ точек пересечения N иM прямой a с поверхностью призмы.

5. Находим точки N₂ и M₂: N₂ 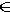 a₂, M₂  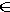a₂ с помощью линий связи. Точки N₂ и M₂ — вторые проекции искомых точек пересечения прямой а с поверхностью призмы.

6. Определяем видимость прямой с помощью метода конкурирующих точек.