§ 4. Описание работы функции осплт и всех ее аргументов.

Возвращает величину платежа в погашение основной суммы по инвестиции за данный период на основе постоянных периодических платежей и постоянной процентной ставки.

Синтаксис функции: осплт(ставка;период;кпер;пс;бс;тип)

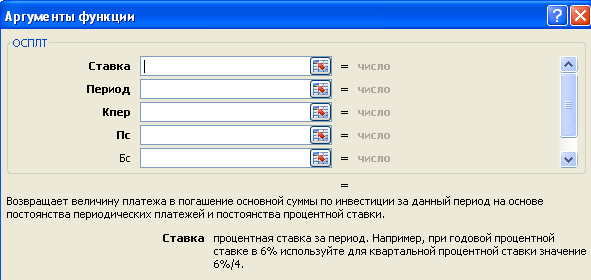
Ставка   — процентная ставка за период.

Период   — период. Значение должно находиться в интервале от 1 до «кпер».

Кпер   — общее число периодов платежей по аннуитету.

Пс   — приведенная к текущему моменту стоимость, т. е. общая сумма, которая на текущий момент равноценна ряду будущих платежей.

Бс   — значение будущей стоимости, т. е. желаемого остатка средств после последней выплаты. Если этот аргумент опущен, то предполагается, что он равен 0 (например, значение «бс» для займа равно 0).

Тип   — число 0 или 1, обозначающее срок выплаты.

Тип	Когда нужно выплатить
0 или опущен	В конце периода
1	В начале периода

При вычислении необходимо убедиться, что для аргументов СТАВКА и КПЕР используются согласованные единицы измерения. Если производятся ежемесячные платежи по четырехгодичному займу из расчета 12% годовых, то ставка должна быть 12%/12 , а кпер должно быть 4*12. Если производятся ежегодные платежи по тому же займу, то ставка должна быть 12%, а кпер должно быть 4.

Пример 1

Ставка	Кпер	ПС	Формула	Описание (Результат)
10%	2	2000	=ОСПЛТ([Ставка]/12, 1, [Кпер]*12, [ПС])	Основной платеж на первый месяц займа равен -75.62

Для получения месячной ставки разделите процентную ставку на 12. Для получения количества платежей умножьте на 12 число лет, в течение которых производятся выплаты.

Пример 2

Ставка	Период	ПС	Формула	Описание (Результат)
8%	10	200,000	=ОСПЛТ([Ставка], [Период], 10, [ПС])	Основной платеж последнего года займа при заданных аргументах равен -27,598.05

§ 5. Набор исходных данных, которые будут использованы для демонстрации работы функции осплт.

Задача 1.

Определить значение основного платежа для первого месяца двухгодичного займа в 60000 руб. под 12% годовых.

Решение задачи:

Данные по задаче представим в виде таблицы:

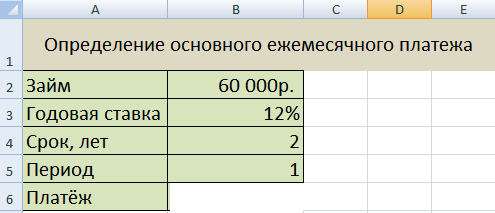
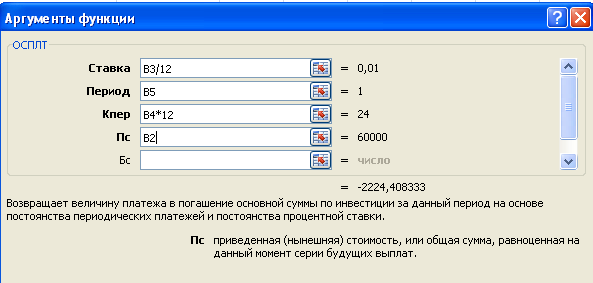
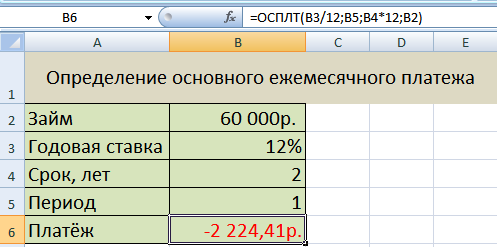
Сумма основного платежа по займу вычисляется с помощью функции ОСПЛТ: = ОСПЛТ (12%/12; 1; 24; 60000) = - -2 224,41руб.

 Знак «минус» в результате означает, что сумму основного долга по займу необходимо внести. Отметим, что сумма выплаты по процентам, вычисляемая с помощью функции ПРПЛТ, и сумма основной выплаты за период, рассчитанная с помощью функции ОСПЛТ, равны полной величине выплаты, вычисляемой с помощью функции ПЛТ.

Готовая таблица имеет вид:

Задача 2

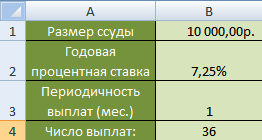
Составить график погашения ссуды, если берётся сумма размером 100000 рублей под 7,25% годовых, с ежемесячной выплатой на три года.

Решение задачи:

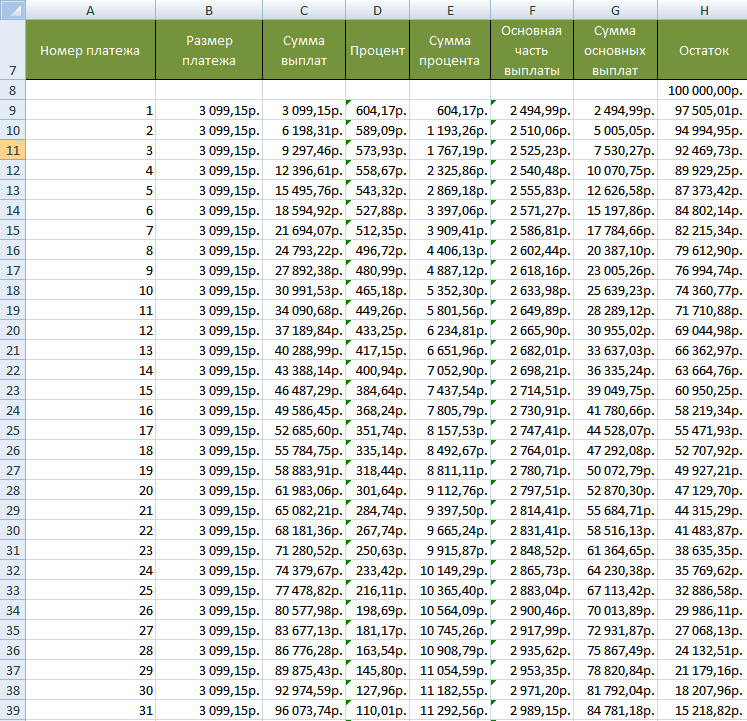
График погашения ссуды представляет собой таблицу, содержащую различную информацию по каждому периоду выплаты.

Начальные данные представим в виде таблицы:

Формулы, используемые для создания графика выплат:

Готовая таблица (график погашения ссуды) имеет вид:

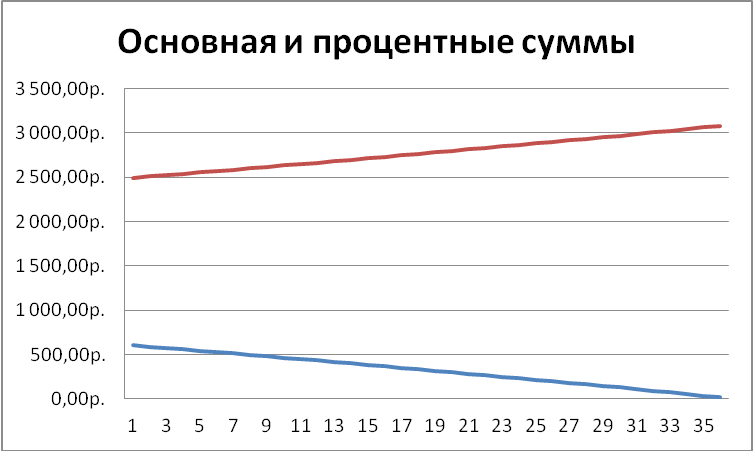
На графике представлены основные и процентные суммы для всего срока платежа:

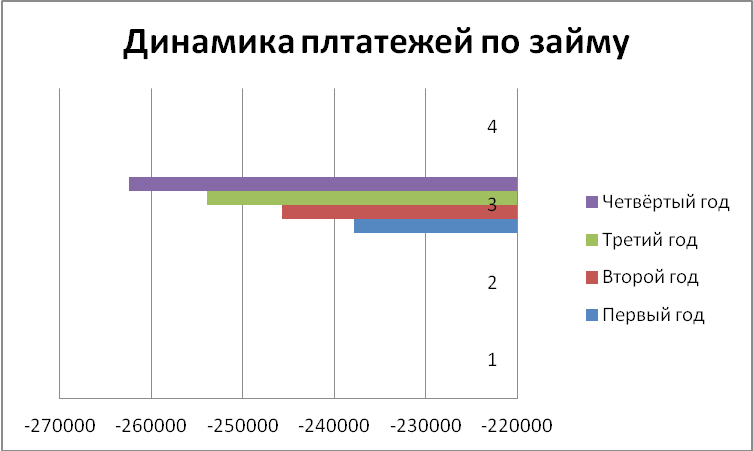
Задача 3

В банке взята в кредит сумма в размере 1000000 руб. Сроком на 4 года при годовой процентной ставке, равной 10 %. Необходимо рассчитать величину платежей по годам за период займа.

Таблица с данными имеет вид:

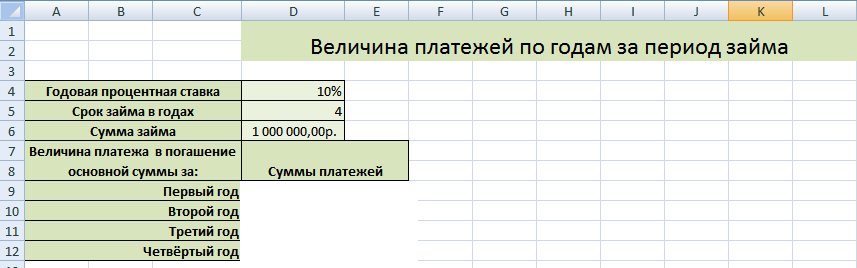
Для расчёта величины платежа за первый год функция ОСПЛТ имеет вид:

ОСПЛТ($D$4*$D$5/12;1;$D$5;$D$6)

Для расчёта величины платежа за второй год функция ОСПЛТ имеет вид:

ОСПЛТ($D$4*$D$5/12;2;$D$5;$D$6)

Готовая таблица имеет вид:

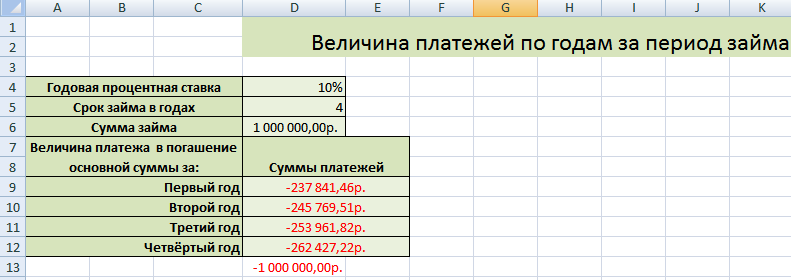
Графическое представление полученных результатов: