
dinamics2
.pdf1
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
РАДИОФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА РАДИОФИЗИКИ
Л.А.Бабенко
ЭЛЕКТРОДИНАМИКА И РАСПРОСТРАНЕНИЕ РАДИОВОЛН
ПОСТАНОВКА ЗАДАЧ ЭЛЕКТРОДИНАМИКИ. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ.
ВОЛНОВЫЕ ЯВЛЕНИЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД
Конспект лекций. Часть II
2006
2
Содержание
1.Постановка задач электродинамики. Теорема единственности для задач электродинамики. Электродинамические потенциалы. Волновое уравнение. Простейшее решение волнового уравнения. Плоские волны. Сферические волны.
Запаздывающие потенциалы……………………………………………………….3 - 12
2.Электромагнитные волны в различных средах. Уравнения электродинамики для гармонических колебаний. Гармонические волны Перестановочная двойственность уравнений Максвелла. Магнитные токи. Плоские волны в среде без потерь. Скорость переноса энергии. Групповая скорость. Плоские волны в среде с потерями (диэлектрик с малыми потерями, хороший проводник).
Поляризация плоских волн…………………………………………………………13 - 27
3. Волновые явления на границе раздела двух сред. Законы Снеллиуса.
Приближенные граничные условия Леонтовича - Щукина. Формулы Френеля. Наклонное падение волны на проводящую поверхность. Плоский полый волновод. Волны вдоль плоской границы диэлектриков. Плоский диэлектрический волновод
……………………………………………………………. ………………………... 27 - 42
3
Теорема единственности для задач электродинамики.
Система основных уравнений Максвелла является полной, т.е. электромагнитное поле в каждой точке пространства и в каждый момент времени однозначно определяется этой системой, если только для момента t=t0 заданы начальные значения векторов E иH во всех точках пространства. Однако определить напряженность во всем бесконечном пространстве невозможно, т.к. наблюдению доступна лишь его ограниченная часть. Поэтому теорема единственности становится необходимой, если ограничиться некоторым конечным объемом пространства и дополнить условия, определяющие решение уравнений Максвелла, граничными условиями на границах раздела этого объема.
В качестве первичной причины существования электромагнитного поля естественно видеть превращение неэлектромагнитной энергии в энергию поля. Поэтому будем исследовать решения при заданных источниках, т.е. такие, которые должны представлять вынужденные поля.
Теорема единственности утверждает, что электромагнитное поле в любой момент времени t>t0 в любой точке объема V, ограниченного поверхностью S, определяется уравнениями Максвелла однозначно, если в каждой точке объема V заданы начальные значения векторов E(r , t0 ) = E0 , H(r , t0 ) = H0 и если известны граничные значения проекций, касательных к S, одного из векторов E или H в
точках поверхности S для любого момента времени t>t0.
Для доказательства теоремы предположим, что для области V, содержащей источники поля j s , существуют два решения уравнений Максвелла,
удовлетворяющие одинаковым начальным и граничным условиям. Обозначим поля,
соответствующие этим решениям, через E1, H1 и E2 , H2 . Очевидно, что разность указанных решений E ′ = E1 − E2 , H ′ = H1 − H2 удовлетворяет уравнениям Максвелла, не содержащим источники, а также нулевым начальным и граничным условиям
E ′(r , t0 ) = 0, |
H ′(r , t0 ) = 0, |
E ′ × n0 |
S |
= 0, H ′ × n0 |
S |
= 0 |
|
|
|
|
|
Применим к полю E ′, H ′теорему Пойнтинга:

4
|
2 |
|
|
d |
|
ε |
0 |
εE ′2 |
|
µ |
0 |
µH ′2 |
|
∫σE ′ |
dv + ∫ |
E ′ × H ′ ds + |
|
|
|
|
+ |
|
|
|
|||
|
dt |
∫ |
|
|
2 |
|
|
2 |
dv = 0 |
||||
V |
|
S |
|
V |
|
|
|
|
|
|
Так как ds = n0ds, то, учитывая граничные условия для полей E ′, H ′, получаем, что
интеграл по поверхности S равен нулю. Очевидно, что интеграл ∫σE ′2 dv всегда
V
больше или равен нулю. Следовательно, уравнение баланса энергии будет удовлетворено лишь в том случае, когда функция
W(t) = 1 ∫(ε0εE ′2 + µ0µH ′2 )dv
2 V
монотонно убывает во времени (только при этом предположении |
∂W |
≤ 0). Но при |
|
∂t |
|||
|
|
t=t0 энергия поля W(t0) = 0 . Так как энергия электромагнитного поля не может принимать отрицательные значения, то уравнение баланса будет справедливо лишь при условии, что функция W(t) = 0 для любого t ≥ t0. Последнее возможно, если E ′
и H ′равны |
нулю в каждой точке области V при t ≥ t0. Следовательно, |
E1 = E2 = E, |
H1 = H2 = H, что доказывает единственность решения. |
Исследованная задача о нахождении поля внутри объема V называется внутренней задачей электродинамики. Все рассуждения можно повторить и для внешней задачи, когда вынужденное поле существует в бесконечном пространстве вне некоторой области V ′. Теперь V – область, ограниченная изнутри поверхностью S, а из вне – поверхностью сферы бесконечно большого радиуса S r. В этом случае теорема Пойнтинга для поля E ′и H ′ запишется в виде
∫σE ′2dv + ∫ E ′ × H ′ ds + ∫ E ′ × H ′ ds + |
d |
|
ε |
0 |
εE ′2 |
|
µ |
0 |
µH ′2 |
|
||
|
∫ |
|
2 |
+ |
|
2 |
dv = 0. |
|||||
V |
S |
S |
dt V |
|
|
|
|
|
|
|||
|
|
r |
|
|
|
|
|
|
|
|
|
|
Проведенные выше рассуждения полностью применимы и к последнему равенству
при условии, что 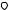 ∫ E ′ × H ′ n0ds → 0 при r→∞.
∫ E ′ × H ′ n0ds → 0 при r→∞.
Sr
Но, если с момента возникновения поля прошел конечный промежуток времени, можно утверждать, что поверхность Sr лежит вне той области, которую заняло поле

5
к моменту t > t0, распространяясь в пространстве с конечной скоростью. В этом случае последнее условие, безусловно, удовлетворяется.
Итак, рассмотрен вопрос о необходимых и достаточных условиях для единственности решения уравнений Максвелла в общем случае произвольной зависимости векторов E, H от времени. В эти условия входят как условия на границе, так и начальные условия, требующие задания поля во всем пространстве для момента t = 0. Однако необходимость в задании начальных значений поля отпадает, если речь идет о решении для так называемого установившегося режима, когда составляющие поля меняются со временем по периодическому закону.
Электродинамические потенциалы. Волновое уравнение.
Рассмотрим некоторые методы подхода к решению прямых задач электродинамики. В этих задачах требуется найти векторы электромагнитного поля по заданным источникам.
Прежде всего, получим уравнения для каждого из векторов E и H по отдельности.
Умножим все члены первого уравнения Максвелла на εr-1, а второе – на µr -1 и
применим к векторам операцию rot (т.е. ×g ):
× (εr −1 × H )= ε0 ∂∂t ( × E)+ × εr −1 j,× (µr −1 × E)= −µ0 ∂∂t ( × H )
Заменим × E и × H в правых частях уравнений выражениями, вытекающими из первых двух уравнений Максвелла. В результате получим
µ |
|
2 |
|
|
|
|||
× (εr −1 × H )+ |
|
r |
|
∂∂tH2 = × εr −1 j , |
||||
c2 |
||||||||
× (µr −1 × E)+ |
ε |
|
∂2 E |
|
∂ j |
|
||
r |
|
∂t 2 |
= −µ0 |
|
, |
|||
c 2 |
|
∂t |
||||||
6
где обозначено εо µо = с –2. Правые части этих уравнений в общем случае нельзя рассматривать как известные. Для идеального диэлектрика, когда σ = 0, j = j s и
правые части определяются заданными источниками. Если среда однородна
(εr = const , µr = const), уравнения могу быть записаны в виде
|
|
|
|
2 H − |
εr µr |
∂2 H |
= − × j |
|
|
|||||||
|
|
|
|
c2 |
|
|
||||||||||
|
|
|
|
|
|
|
∂t 2 |
|
|
|
|
|
||||
|
|
2 |
E − |
|
εr µr |
∂2 E |
= − |
|
1 |
|
ρ + µ0µr |
∂ j |
|
|||
|
|
|
c2 |
∂t 2 |
ε |
|
|
∂t |
||||||||
|
|
|
|
|
|
|
0εr |
|
||||||||
Здесь использовано тождество × ( × a) = ( a) − 2a |
|
|
||||||||||||||
и учтено также, что |
H = 0, E = ρ (ε0εr ) . Если |
j = j s , то ρ = ρs , причем эти |
||||||||||||||
величины связаны законом сохранения заряда. |
|
|
|
|
|
|||||||||||
Таким образом, для |
каждого из векторов |
E и H |
получено уравнение второго |
|||||||||||||
порядка. Уравнения с левыми частями такого вида называются уравнениями Даламбера. Уравнения позволяют найти векторы электромагнитного поля по заданным источникам. Однако из-за сложности правых частей эти уравнения оказываются неудобными для решения задачи. Обычно их используют в тех случаях, когда в рассматриваемой области нет сторонних источников, т.е. когда они являются однородными. Такие уравнения называются волновыми.
В общем случае решение задачи существенно упрощается, если предварительно определить некоторые вспомогательные функции, которые принято называть электродинамическими потенциалами. Их можно ввести различным образом в зависимости от специфических особенностей анализируемой задачи, однако, принцип их построения один и тот же.
Уже был введен векторный потенциал B = × A, A- векторный потенциал. При
известном векторе A вектор B определяется однозначно. Вектор A определен с точностью до градиента произвольной скалярной функции. Вектор напряженности магнитного поля
H = |
1 |
× A. |
|
||
|
µ0µr |
|
7
Подстановка этого выражения H во второе уравнение Максвелла приводит к равенству × (E + ∂∂At ) = 0 . Векторная функция, стоящая в скобках, является
потенциальной. Приравняв эту функцию величине - ϕ, получаем
E = − ϕ − ∂∂At
Таким образом, векторы, характеризующие электромагнитное поле, выражаются через две функции: векторный потенциал A и скалярный потенциал ϕ. Остается найти уравнения, которым они удовлетворяют.
Заменим в первом уравнении Максвелла напряженности поля их выражениями через потенциалы. Для однородной среды получаем
|
|
|
× ( × A) + |
εµ ∂2 A |
= − |
εµ |
|
∂ϕ |
+ µ0µ j |
|
|
|||||||||||||
|
|
|
c2 ∂t 2 |
c |
2 |
∂t |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Заменим |
первое |
|
слагаемое |
при |
|
|
помощи |
векторного |
тождества |
|||||||||||||||
× ( × a) = ( a) − 2a , введем оператор Лапласа. Это дает |
|
|
||||||||||||||||||||||
|
|
2 |
|
ε |
r |
µ |
r |
∂ |
2 |
A |
ε |
r |
µ |
r |
∂ϕ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
A − |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
+ A − µ0µr |
j |
|
|||
|
|
|
c2 ∂t |
2 |
|
|
|
|
∂t |
|
|
|||||||||||||
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|||||||||||
Упростим это уравнение. Уже отмечалось, что вектор |
A определен с точностью до |
|||||||||||||||||||||||
градиента произвольной скалярной функции. Следовательно, можно потребовать,
чтобы вектор |
удовлетворял |
добавочному |
условию. |
Потребуем, |
чтобы |
||||||||
A + |
εr µr |
∂ϕ |
= 0 . Это уравнение |
называют |
условием |
калибровки |
(или |
||||||
c2 |
∂t |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
калибровкой Лоренца). При этом для потенциала A получаем векторное уравнение |
|||||||||||||
Даламбера |
|
|
2 |
A − |
|
εr µr |
∂2 A |
= −µ0µr j |
|
|
|||
|
|
|
c2 |
∂t 2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогичное уравнение получаем для скалярного потенциала ϕ. Подставив в третье уравнение Максвелла выражение вектора E через потенциалы и, используя условие калибровки, приходим к уравнению
8
2ϕ − εµ ∂2ϕ |
= − |
ρ |
|
ε0ε |
|||
c2 ∂t 2 |
|
Таким образом, векторный и скалярный потенциалы, как и векторы E и H , удовлетворяют неоднородным уравнениям Даламбера. Однако правые части уравнений для потенциалов имеют более простой вид. Скалярный потенциал ϕ зависит лишь от распределения зарядов, а векторный потенциал A - от распределения токов проводимости.
Простейшее решение волнового уравнения. Плоские волны.
Предположим, что в рассматриваемой области пространства сторонние силы не действуют. Если при этом найдено физически осмысленное решение уравнений поля, то оно выражает свободное электромагнитное поле, т.е. поле, не обязанное своим происхождением процессу преобразования какого либо вида энергии в электромагнитную. В отсутствии сторонних источников любая декартова компонента векторов E и H удовлетворяет однородному волновому уравнению
2u − |
1 |
∂2u |
= 0. |
|
|||
|
v 2 ∂t 2 |
|
|
Рассмотрим его решение, зависящее только от одной координаты z и времени t. Для u = u (z,t) справедливо уравнение
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∂ u |
|
1 |
∂ u |
|
∂ |
|
1 ∂ |
∂ |
|
1 ∂ |
|||||||||||
− |
= 0, |
или |
− |
|
+ |
u(z, t) = 0, |
|||||||||||||||
|
2 |
|
2 |
|
2 |
∂z |
|
|
|
∂z |
|
|
|
||||||||
∂z |
|
v |
∂t |
|
|
|
v ∂t |
|
v ∂t |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в котором оператор Даламбера записан в виде произведения двух сомножителей.
Введем новые переменные ξ == z − vt; η = z + vt, так, |
что обратное преобразование |
|||||||||||||||||||||||||||||||
даст z = |
ξ + η |
, |
t = |
η − ξ |
. Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
2v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
∂ |
= |
∂z ∂ |
+ |
∂t |
|
∂ |
|
= |
1 ∂ |
− |
1 ∂ |
, |
∂ |
= |
1 ∂ |
+ |
1 ∂ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
∂ξ ∂z |
∂ξ ∂t |
2 ∂z |
2v ∂t |
∂η |
2 ∂z |
2v ∂t |
||||||||||||||||||||||
|
|
|
∂ξ |
|
|
|
|
|
|
|||||||||||||||||||||||

|
|
|
|
|
|
|
|
|
9 |
В результате волновое уравнение в новых переменных принимает вид |
∂2u(ξ, η) |
= 0. |
|||||||
|
∂ξ∂η |
||||||||
|
|
|
|
|
|
|
|
|
|
Проинтегрируем уравнение по переменной ξ: |
|
∂u(ξ, η) |
|
= F(η) . Интегрируя еще раз |
|||||
|
∂η |
||||||||
|
|
|
|
|
|
|
|
||
по переменной η, находим u(ξ, η) = g(η) + h(ξ). Здесь |
|
∂g(η) |
= F(η), |
|
h(ξ) играет |
||||
|
∂η |
|
|||||||
|
|
|
|
|
|
|
|
|
|
роль постоянной интегрирования по η, |
которая может |
зависеть |
от второй |
||||||
переменной как от параметра. Вид функций g и h не определяется из решения уравнения, а устанавливается путем задания начальных условий.
Возвратившись к исходным переменным, получим u(z, t) = g(z + vt) + h(z − vt),
т.е. решение уравнения представляет собой наложение двух возмущений, каждое из которых распространяется вдоль z в сторону возрастания или убывания z со
скоростью v u(z, t) = u+ (t − z v) + u− (t + z v),
u±- произвольные дважды дифференцируемые функции.
Это математическое описание некоторого волнового процесса. При распространении волны среда вовлекается в физический процесс, в результате чего происходит передача энергии в пространстве. Пусть физический процесс в точке
M (r1) характеризует функция u(r1, t) = f (t). В другой точке |
P(r2 ) процесс не |
наблюдается, т.е. u = 0, пока он не передан средой. Потом |
u(r2 , t) = f1(t). В |
простейшем случае в точке Р обнаружится лишь запаздывание, т.е. f1(t) = f (t − τ),
где τ - время прохождения пути r2 − r1 = l со скоростью v.
Если изменения в пространстве происходят только в направлении z, то процесс
характеризуется волной u(z, t) = f (t − z v). |
При z = 0 |
u(0, t) = f (t) , при |
z = l |
u(l, t) = f (t − l v) = u(0, t − l v) - временная |
зависимость, |
отличающаяся |
только |
сдвигом. Рассмотренный волновой процесс – бегущая плоская однородная волна в среде, которая ее не деформирует (в любой точке плоскости z=const процесс описывается этой функций). Считая v положительной величиной, для волны, движущейся в направлении, противоположном z, надо заменить аргумент

10 u(z, t) = f (t + z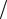 v). Итак, общее решение волнового уравнения можно представить в виде наложения прямой и обратной волн.
v). Итак, общее решение волнового уравнения можно представить в виде наложения прямой и обратной волн.
Определим взаимную ориентацию векторов E, H в плоской волне. Для векторного
потенциала A справедливо волновое уравнение. Для описания поля в отсутствии
зарядов можно выбрать такую |
калибровку потенциалов, при которой |
ϕ = 0 |
||||
тождественно, а также A = 0. При этом, полагая A = A(z, t), получаем |
∂Az |
= 0 . |
||||
|
||||||
|
|
|
|
|
∂z |
|
Поскольку z входит в аргумент |
A в линейных комбинациях (z ± vt) , последнее |
|||||
равенство дает Az = const (z,t). Следовательно |
|
|
|
|||
Ez = − |
∂Az |
= 0,H z = |
1 |
( × A)z = 0 . |
|
|
∂t |
|
|
|
|||
|
|
µ0µr |
|
|
||
Проекции напряженностей поля на направление распространения отсутствуют – плоские электромагнитные волны поперечны.
Далее предположим, что волна бежит в одну сторону A(z, t) = A(z − vt) . При этом
|
∂A |
|
c ∂A |
|
|
|
|
1 |
|
|
1 |
|
|
|
∂Ay |
|
|
|
∂A |
x |
|
|
||
E = − |
|
= |
|
, |
|
H = |
|
|
× A = |
|
|
|
− x |
0 |
|
|
+ y |
0 |
|
|
|
= |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂t |
|
εr µr ∂z |
|
|
|
|
µ0µr |
|
|
|
|
|
∂z |
|
|
∂z |
|
|
|||||
|
|
|
|
|
|
|
|
µ0µr |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
= |
|
1 |
z0 × |
∂A = |
ε0εr |
z0 × E |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
µ0µr |
∂z |
µ0µ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
В плоской волне |
векторы |
E |
и |
H |
взаимно ортогональны |
и |
|
ортогональны |
||||||||||||||||
направлению распространения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Сферические волны.
При наличии сферической симметрии решение волнового уравнения можно получить в виде сферических волн. Предположим, что поле создается точечным зарядом, расположенным в начале координат. Величина этого заряда меняется со временем q=q (t). В любой точке, кроме начала координат, потенциал ϕ удовлетворяет однородному уравнению Даламбера. Вне области, занятой источником, волновое уравнение принимает вид
