3. Упругое рассеяние на твердом шаре.

Найдем полное сечение рассеяния на твердом шаре радиусом , используя выражение (15.8).

Воспользовавшись рисунком, получаем связь между параметрами и :

.

Теперь вычисляем производную:

и, подставляя в выражение (15.8), получаем

дифференциальное сечение рассеяния:

,

или через телесный угол с вершиной в центре шара:

. (15.13)

Из (15.13) следует, что рассеяние в системе изотропно.

Полное сечение рассеяния на твердом шаре равно

. (15.14)

Т.о., прицельная площадь, куда должна попасть частица, чтобы рассеяться, равна площади сечения шара.

4. Кулоновское рассеяние.

Рассеяние заряженных частиц на кулоновском центре описывается формулой Резерфорда. Получим эту формулу, принимая в расчет, что связь между параметрами столкновения (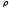, 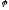и ) дается формулой (15.4). Используя (15.4), запишем квадрат прицельного параметра, продифференцируем полученное выражение и подставим результат в формулу (15.7), выражающую сечение рассеяния через прицельное расстояние:

,

.

Для эффективного сечения имеем (15.7)

.

И окончательно для эффективного сечения рассеяния получаем выражение вида:

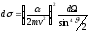. (15.15)

Для рассеяния частиц на ядрах элементов с порядковым номером , подставляя в (15.15) , приходим к знаменитой формуле Резерфорда:

. (15.16)

Для сравнения расчетного значения с экспериментом необходимо еще просуммировать по числу ядер в единице объема (1 см³) образца (фольги), и, если ядра не перекрывают друг друга, то измеряемое сечение будет равно

(15.17)

В эксперименте Резерфордом проверялась следующая величина:

. (15.18)

Условия эксперимента не менялись, поэтому правая часть уравнения (15.18) остается постоянной и число рассеянных под углом частиц должно быть пропорционально .

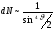Т.о., путем сравнения результатов, полученных в опытах Резерфорда, и их сравнением с формулой Резерфорда удалось установить, что частицы рассеиваются в поле, создаваемом точечным центром с положительным зарядом ядро атома.