46

Непрерывность функции. Классификация точек разрыва.

Определение 1. Функция f(x) называется непрерывной в точке х₀, если

(1)

Это означает, что функция f(x) удовлетворяет следующим условиям:

1. определена в точке х₀ (т.е. существует f(x₀));

2. имеет конечный предел функции при х→х₀;

3. этот предел равен значению функции в точке х₀, т.е.

Т.к. =x₀, то равенство (1) можно придать следующую форму:

- т.е. предел функции равен значению функции от предела аргумента. Т.о. для непрерывной функции возможна перестановка символов предела и функции.

Определение 2. Функция f(x) называется непрерывной в точке х₀, если любому, сколь угодно малому, >0 можно указать такое число δ>0 (зависящее от , δ=δ()), что для всех хХ таких, что |x-x₀|<δ выполняется неравенство |f(х)- f(x₀)|<.

>0 δ=δ() x: |x-x₀|<δ |f(х)- f(x₀)|<

(Здесь нет запрета х≠х₀).

Определение 3 (в терминах окрестности). Функция f(x) называется непрерывной в точке х₀, если для любого сколь угодно малого числа >0 найдется такое число δ=δ(Е), что для всех х, попадающих в -окрестность точки х₀, соответствующие значения функции попадают в -окрестность величины f(x₀) (здесь окрестность не выколотая):

W(f(x₀)) V(x₀): x V(x₀)f(х)W(f(x₀)) (рисунок)

Определение 4 (в терминах последовательности). Функция f(x) называется непрерывной в точке х₀, если для любой последовательности {x_n}, сходящейся к х₀, последовательность {f(x_n)} соответствующих значений функции сходится к f(x₀). (Здесь нет запрета x_n≠x₀).

Пример.

а) у=в точке х=0 не определена.

б) у=не существует предела в точке х=0 (существуют только односторонние пределы: слеваи справа).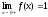

в) у==1.

г) у=х² – непрерывная функция в точке х=0, т.к. выполнены все 3 условия непрерывности.

Примеры разрывных функций.

1) f(x)=sign x, f(x)=

Не существует . В точке х₀=0 функция разрывна.

Замечание. Пусть х₀Х и хХ и пусть х=х₀+∆х, следовательно ∆х=х-х₀.

Величина ∆х называется приращением аргумента (∆х может быть как положительной, так и отрицательной).

Пусть у₀=f(x₀), y=f(x)=f(x₀+∆x).

Величина ∆y=f(x)-f(x₀)=f(x₀+∆x)-f(x₀) называется приращением функции f(x) в точке х₀, соответствующим приращению аргумента х (∆у может быть как положительной, так и отрицательной).

Предположим, что функция f(x) – непрерывна в точке х₀. Это означает, что

или =0, или.

Следовательно, можно сказать, что

Теорема. Функция у=f(x) будет непрерывной в точке х₀ тогда и только тогда, когда бесконечно малому приращению аргумента х соответствует бесконечно малое приращение функции у, т.е. =0.

Эта теорема дает эквивалентное определение непрерывности.

Аналогично определению правостороннего и левостороннего пределов функции f(x), можно определить правостороннюю и левостороннюю непрерывность функции f(x) в точке х₀.

Определение. Функция f(x) называется непрерывной справа в точке х₀, если

.

Функция f(x) называется непрерывной слева в точке х₀, если .

Утверждения. 1) Если функция f(x) непрерывна в точке х₀ в обычном смысле, то она непрерывна в этой точке одновременно и справа, и слева.

2) Если функция f(x) непрерывна в точке х₀ одновременно и справа, и слева, то она непрерывна в этой точке и в обычном смысле.

Определение. Функция f(x) непрерывна на множестве Х, если она непрерывна в каждой точке этого множества.

Определение. Пусть функция f(x) определена на отрезке [a,b]. Функция f(x) непрерывна на [a,b], если она непрерывна в обычном смысле в каждой внутренней точке этого промежутка и если она непрерывна справа в точке а и непрерывна слева в точке b.