67

Основные теоремы дифференциального исчисления.

Локальные экстремумы.

Определение. Точка х₀ называется точкой локального максимума (минимума) функции f(x), если существует такая окрестность точки х₀, что для всех точек х из этой окрестности справедливо неравенство:

V(x₀): xV(x₀)\{x₀} f(x)≤f(x₀) (f(x)≥f(x₀))

Или f(x₀+∆х)≤f(x₀) (f(x₀+∆х)≥f(x₀))

Если выполняется неравенство f(x₀+∆х)<f(x₀) (f(x₀+∆х)>f(x₀)),

То говорят, о строгом локальном максимуме (минимуме).

Значение функции в точке х₀ называют максимумом (минимумом) функции.

Максимум и минимум функции называют экстремумом, х₀ – точка локального экстремума.

Теорема Ферма. (Необходимое условие экстремальных точек) Пусть функция f(x) определена на интервале (a;b) и в некоторой точке х₀ этого интервала имеет наибольшее или наименьшее значение (локальный экстремум). Тогда, если в точке х₀ существует производная, то она равна нулю =0

Доказательство. Пусть для определенности в точке х₀ функция имеет наибольшее значение, т.е. f(x)≤f(x₀) .

Это значит, что ∆у=f(x₀+∆х)-f(x₀)≤0 для любой точки x₀+∆х.

Поэтому, если ∆x>0 (x>x₀),то .

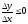Следовательно,

Если же ∆x<0 (x<x₀),то .

Поэтому,

Т.е. правая производная в точке х₀ неположительная, а левая неотрицательна. По условию существует. Значит, ===0. Ч.т.д.

Геометрическая интерпретация теоремы Ферма состоит в том, если в точке x₀.функция f(x) принимает наибольшее или наименьшее значение, то касательная к графику функции у=f(x) в точке (х₀,f(x₀)) параллельна оси Ох. (Рисунок).

Теорема Ролля. Пусть функция y=f(x) определена и непрерывна на отрезке [a;b], дифференцируема хотя бы в интервале (a;b).

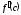Если f(a)=f(b), то найдется, по крайней мере, одна такая точка с(a;b), что =0.

Доказательство.

Т.к. функция y=f(x) непрерывна на отрезке [a;b], то по теореме Вейерштрасса, функция f(x) на отрезке [a;b] достигает как своего наибольшего М, так и своего наименьшего m значения. Значит х[a,b] mf(x)M (1)

Возможны 2 случая

1. Если m=M, то из неравенства (1) следует, что все значения функции f(x) в промежутке [a;b] равны между собой, т.е. f(x)=const, тогда с – любая точка интервала (a;b).

2. m<M, т.е. f(x)≠const. В этом случае хотя бы одно из двух значений m или M функция f(х) принимает во внутренней точке с(a;b) (иначе, ввиду того, что f(a)=f(b), мы получили бы m=M, а это не так).

Т.о. выполнены все условия теоремы Ферма. Значит =0. Ч.т.д.

Геометрический смысл теоремы Ролля.

Если крайние ординаты графика функции у=f(x) равны, то на кривой найдется хотя бы одна точка, в которой касательная к графику функции у=f(x) будет параллельна оси абсцисс. В этой точке производная и будет равна нулю.

Рисунок.

Пример. 1) Пусть f(x)=х²-4х.

f(0)=f(4)=0 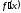=2x-4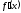=0 в точке х=2. Здесь a=0, b=4, c=2.

2) Пусть f(x)=х³-6х²+11х-6.

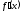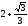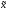f(1)=f(2)=f(3)=0 =3x²-12х+11=0 в точках ₁=, ₂=.

Здесь точка ₁= лежит между точками х₂=2 и х₃=3,

Точка ₂=. лежит между точками х₁=1 и х₂=2.

Теорема Лагранжа о конечных приращениях.

Пусть 1) функция y=f(x) определена и непрерывна на отрезке [a;b], 2) существует конечная производная 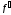(х), по крайней мере, на интервале (a;b), тогда найдется по крайней мере одна точка с(a;b) такая, что

с(a;b): что f(b)-f(a)=(c)(b-a)

или

Доказательство.

1. При f(a)=f(b) утверждение вытекает из теоремы Ролля. (0=0(b-a))

2. При f(a)≠f(b). Введем вспомогательную функцию.

Вычтем из функции f(x) линейную функцию φ(х) такую, чтобы значение разности f(x)-φ(х) на концах отрезка совпадали.

Проведем прямую L׀׀AB, тогда

φ(х)=

Тогда f(а)-φ(а)= f(а)-0= f(а)

f(b)-φ(b)=f(b)-f(b)+f(a)=f(a)

Введем функцию g(x)=f(x)-,

g(a)=f(a)=g(b)

Функция g(x) удовлетворяет условиям теоремы Роля: непрерывна в [a;b], т.к. представляет собой разность между непрерывной функцией f(x) и линейной функцией. В промежутке (a;b) имеет конечную производную, равную (х)=(х)-. Следовательно, модно применить теорему Роля, т.е.

с(a;b): что (c)=0

(c)=(с)- =0, т.е. ч.т.д.

- формула Лагранжа или формула конечных приращений.

Геометрический смысл теоремы Лагранжа. Пусть A(a,f(a)) и B(b,f(b)) – концы графика функции y=f(x), АВ – хорда, соединяющая точки А и В. Тогда правая часть формулы 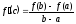представляет собой tg , т.е. тангенс угла, образованного хордой АВ с положительным направлением оси Ох.

Поэтому равенство можно переписать в виде tg =tg . Значит, на кривой АВ имеется, по крайней мере, одна точка (c,f(c)) такая, в которой касательная к АВ параллельна хорде АВ.

Следствие 1.

Пусть функция у=f(x) дифференцируема в каждой точке промежутка (a;b). Если (х)=0 х(a;b), то функция тождественно постоянна на этом промежутке (f(x)=const).

Доказательство.

Зафиксируем точку х₀(a;b) и возьмем точку х правее х₀. Тогда, по теореме Лагранжа, f(x)-f(x₀)=(c )(x-x₀). Т.к. (с)=0, то f(x)-f(x₀)=0. Т.е. для всех х правее х₀ f(x)=f(x₀).

Аналогично, если х левее х₀, то f(x₀)-f(x)=0, т.е. f(x₀)=f(x). Ч.т.д.

Следствие 2.

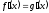
Пусть функции f(x) и g(x) такие, что х(a;b).

Тогда функция f(x)-g(x)=const)

Теорема Коши. (б.д.)Пусть имеются две функции f(x) и g(x), удовлетворяющие условиям:

1) f(x) и g(x) определены и непрерывны на отрезке [a;b];

2) f(x) и g(x) имеют конечные производные и хотя бы в интервале (a;b);

3) .

Тогда между точками a и b найдется по крайней мере одна точка с такая, в которой имеет место равенство: - формула Коши.

Доказательство. Установим сначала, что знаменатель не равен нулю, т.е. g(a)≠g(b). Действительно, если предположить, что g(a)=g(b), то функция g(x) будет удовлетворять условиям теоремы Ролля. Тогда найдется хотя бы одна точка такая, что =0. А это невозможно, т.к. по условию .

Рассмотрим вспомогательную функцию

F(x)=f(x)-f(a)-, которая удовлетворяет условиям теоремы Ролля, а именно 1) определена и непрерывна на отрезке [a;b], т.к. f(x) и g(x) определены и непрерывны на отрезке [a;b];

2) имеет конечную производную хотя бы в интервале (a;b), .т.к. в (a;b) существуют конечные производные и ;

3) F(а)=f(а)-f(a)-=0=F(b)=f(b)-f(a)-=0

Следовательно, обязательно найдется хотя бы одна точка с(a;b): , т.е.

 ч.т.д.

Замечание 1. Формула конечных приращений Лагранжа является частным случаем формулы Коши при g(x)=x, x[a,b].

Замечание 2. Как формула Коши, так и формула Лагранжа, имеет место не только когда a<b, но и в случае, когда a>b