-
Морфологическая реконструкция
Суть
ее в применении операции расширения.
Она базируется на двух изображениях,
называемых маркером и маской. Под маской
можно понимать исходное изображение,
а под маркером связанное с ним изображение,
основанное на параметрах исходного.
Например, маркер может быть получен из
исходной маски вычитанием некоторого
постоянного числа
.
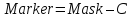10
10 10 10 10 10 10 10 10 10
10
14 14 14 10 10 11 10 11 11
10
14 14 14 10 10 10 11 10 10
10
14 14 14 10 10 11 10 11 10
10
10 10 10 10 10 10 10 10 10
10
11 10 10 10 18 18 18 10 10
10
10 10 11 10 18 18 18 10 10
10
10 11 10 10 18 18 18 10 10
10
10 10 10 10 10 10 10 10 10
10
10 10 10 10 10 11 10 10 10
8
8 8 8 8 8 8 8 8 8
8
12 12 12 8 8 9 8 9 8
8
12 12 12 8 8 8 9 8 8
8
12 12 12 8 8 9 8 9 8
8
8 8 8 8 8 8 8 8 8
8
9 8 8 8 16 16 16 8 8
8
8 8 9 8 16 16 16 8 8
8
8 9 8 8 16 16 16 8 8
8
9 8 9 8 8 8 8 8 8
8
8 8 8 8 8 9 8 8 8
10
10 10 10 10 10
11
10 10 10
10
12 12 12 10
10
10
10
10
10
10
12 12 12
10
10
10
10
10
10
10
12 12 12
10
10
10
10
10
10
10
10 10 10 10 10 10
10 10 10
10
10
10
10 10
16
16 16
10
10
10
10
10
10 10
16
16 16
10
10
10
10
10
10 10
16
16 16
10 10
10
10
10
10 10 10 10
10 10 10
10
10 10 10 10 10 10
10 10 10
Реконструкцию
можно использовать для заполнения
внутренних областей объектов. При этом
считаем, что эти внутренние области
принадлежат фону. Таким образом можно
залить внутренние «дырки» объектов:
Исходное изображение преобразуется в маску помощью инверсии Mask = 255 – I. В этой маске края изображения дополняются строками и столбцами, содержащими максимальное значение яркости.
Из исходного изображения делается маркер того же размера, но с нулевыми элементами для всего изображения. Маркер также дополняется такими же строками и столбцами.
После
чего производится морфологическая
реконструкция. В качестве структурного
элемента могут использоваться матрицы
связности. Затем полученный результат
инвертируется.
Алгоритм
заливания
«дырок»
с помощью реконструкции
Пример обнаружение объектов с помощью сегментации изображений
Если
контраст объект-фон является достаточным,
тогда обнаружить такой объект не
представляет труда. Применим средства
выделения границ и морфологические
функции для обнаружения некоторого
медицинского объекта.
Применим
оператор Собеля с
использованием
некоторого
порогового
значения. Выделили точки
контуров.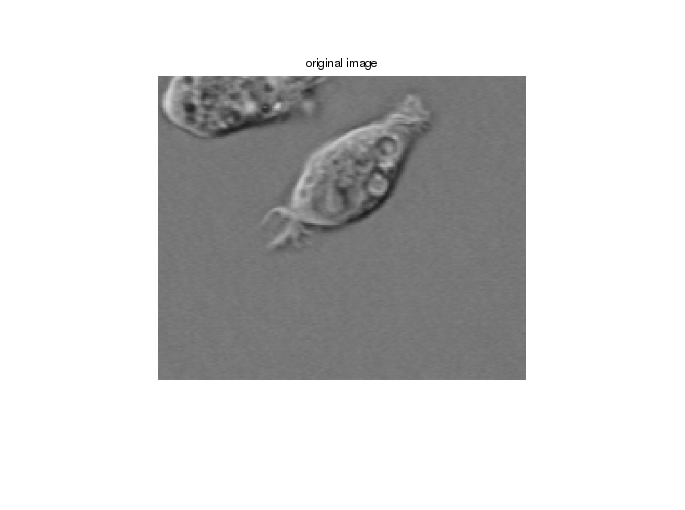
Применим
операцию
расширения Заполняем
«дырки» по рассмотренному
алгоритму Применим
операцию
сужения
для сглаживания
-
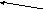
Блочная обработка изображений
Основная идея – найти на изображении блоки с примерно одинаковой интенсивностью и представить его в виде набора этих блоков.
Наиболее просто это делается прямоугольных блоков. Сам алгоритм итеративный и получил название – декомпозиции на основе квадро – деревьев. В нем для каждого рассматриваемого блока определяется параметр, описывающий неоднородность блока. Например это может быть среднее различие интенсивностей (среднеквадратическое отклонение), вычисленный по всему блоку. Однако часто используется относительная разность между максимальной и минимальной интенсивностями в блоке
.
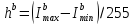Вначале изображение рассматривается как один блок. Затем вычисляется параметр неоднородности и, если он превышает заданный порог, то изображение делится на 4 одинаковых блока. Каждый блок оценивается на однородность. Если оказывается, что он может быть разделен, то он снова делится на 4 блока и так далее. Процесс деления завершается, как только получаются блоки, которые уже невозможно разделить. Иногда такими блоками могут являться отдельные пиксели.
В
алгоритме используются структуры
данных, основанные на квадро-деревьях.
Изображение представляется в виде
разреженной матрицы. Ее элементы
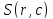соответствующие координатам верхних
левых углов блоков содержат значения,
определяющие размеры соответствующего
блока.
Большинство элементов этой матрицы равно 0, и она удовлетворяет требованиям к разреженным матрицам, допускающим компактное хранение.
1
1 1 1 2 3 6 6
1
1 2 1 4 5 6 8
1
1 1 1 7 7 7 7
1
1 1 1 6 6 5 5
20
22 20 22 1 2 3 4
20
22 22 20 5 4 7 8
20
22 20 20 9 12 40 12
20
22 20 20 13 14 15 16
4
0 0 0 4 0 0 0
0
0 0 0 0 0 0 0
0
0 0 0 0 0 0 0
0
0 0 0 0 0 0 0
4
0 0 0 2 0 2 0
0
0 0 0 0 0 0 0
0
0 0 0 2 0 1 1
0
0 0 0 0 0 1 1
-
Алгоритмы кластерного анализа
Во многих прикладных задачах измерять степень сходства объектов существенно проще, чем формировать признаковые описания. Например, гораздо легче сравнить две фотографии и сказать, что они принадлежат одному человеку, чем понять, на основании каких признаков они схожи.
Задача классификации объектов на основе их сходства друг с другом, когда принадлежность обучающих объектов каким-либо классам не задаётся, называется задачей кластеризации.
Задача кластеризации (или обучения без учителя) заключается в следующем.
Имеется
обучающая выборка
и
функция
расстояния
между
объектами
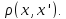Требуется
разбить
выборку
на
непересекающиеся
подмножества,
называемые
кластерами,
так,
чтобы
каждый
кластер состоял из объектов, близких
по метрике
,
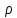а объекты разных кластеров существенно
отличались. При этом каждому объекту
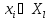приписывается
метка
(номер)
кластера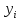
.
Алгоритм
кластеризации это функция
,
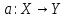которая любому объекту
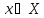ставит
в
соответствие
метку
кластера
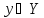. Множество
меток
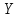в
некоторых
случаях
известно
заранее,
однако
чаще
ставится
задача
определить
оптимальное число кластеров, с точки
зрения того или иного критерия качества
кластеризации.
Решение
задачи кластеризации принципиально
неоднозначно, и тому есть несколько
причин. Во-первых, не существует однозначно
наилучшего критерия качества кластеризации.
Известен целый ряд достаточно разумных
критериев, а также ряд алгоритмов, не
имеющих чётко выраженного критерия, но
осуществляющих достаточно разумную
кластеризацию .по построению.. Все они
могут давать разные результаты. Во-вторых,
число кластеров, как правило, неизвестно
заранее и устанавливается в соответствии
с некоторым субъективным критерием.
В-третьих, результат кластеризации
существенно зависит от метрики
,
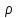выбор которой, как правило, также
субъективен и определяется экспертом.