5. Код Вайнера-Эша

Этот класс кодов аналогичен классу кодов Хэмминга. Он существует для любого m³2. приq>2 n=(m+1),k=(m+1) ,k=(m+1)(2^m-1), если код двоичный. Строится В-Э код на базе проверочной матрицы кода Хэмминга((2^m-1),m). H содержит m-разрядные столбцы, все, кроме нулевого.

Код В-Э задается проверочной матрицей, структура которой следующая:

- строка из (2^m-1) единиц ()

- строки «равные» строкам (соответствующие) проверочной матрице кода Хэмминга.

1. «матрица» 1х1 равная 1

0 - «матрица» 1х1 равная 0

d^* - минимальное расстояние у кода В-Э = 3, значит это код, исправляющий одну ошибку (систематический, логично и Хэмминга брать в систематическом виде, но отнюдь не обязательно)

6. Коды Хэмминга (недвоичные)

d³3, n= 2^m-1; k=2^m-1-m, если код двоичный.

Задается проверочной матрицей все столбцы которой все ненулевые m-разрядные числа.

Когда мы распространяем коды Хэмминга на недвоичные алфавиты, и для построения линейная независимость пар столбцов сохраняется. Но просто различные столбцы уже не гарантируют линейную независимость. Различных линейно независимых будет уже при алфавите q всего . Следовательно, получаются коды Хэмминга с длинамиn =иk=.

Код Хэмминга существует для любого q, для которого существует поле из q элементов GF(q) и любого m>0.

При выборе столбцов, чтобы линейная независимость гарантировалась договоримся брать различные столбцы (m), у которых первая ненулевая компонента =1.

GF(2)	GF(4)	GF(8)	GF(16)	GF(27)
7.4	5.3	9.7	17.15	28.26
15.11	21.18	73.70	273.270	757.754
31.26	85.81	585.581
63.57	341.336
127.120

Примеры: Задайте коды Хэмминга при q=3, m=2,3,...

а) m=2 , k=4-2 (4,2)

d=3

b) m=3 , (13,10)

d=3

Задайте коды Хэмминга при q=4, m=2,3,4...

а) m=2 , k=3 (5,3)

b) m=3 , k=18 (21,18)

Пусть передается информационная последовательность 10000000000000000. Результат кодирования через

Принято

совпадает со столбцом 1. Принято ошибка =1.ошибка в3

m=2 q=16 , (17,15)

Принято из канала

( 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1)

Что передавалось?

• значение ошибки. Ошибка в i₁

В этом разряде передавалось +⁴=1. Итого:

7. Коды Хэмминга как цикличные коды

Первый код из таблиц БЧХ кодов есть код Хэмминга. В качестве g(x) берется многочлен (примитив) по модулю которого строится поле.

Равенство c(x)= m(x) g(x) при x= дает c()=0  это эквивалентно cH^T=0, где H=[1  ²... ^-n-1 ]

Это двоичные коды Хэмминга (n=2^m-1, k=n-m, d3). Ошибочная позиция маркируется элементом поля ⁱ. Условие, когда существует циклический код Хэмминга недвоичный дается теоремой:

Минимальное расстояние кода с проверочной матрицей H=[⁰, ¹,... ,^-n-1 ], где =^q-1 и n=, равно 3 или более, только тогда, когдаn и q-1 взаимно просты, что равносильно m и q-1взаимно просты. Получается что из рассмотренных ранее кодов не все могут быть заданы как циклические. Не циклические, например, код (21,18) поля GF(4).

Задача: Получите порождающий многочлен для кода (85,81) над GF(4). За исходное надо взять поле GF(256) и элемент =³.

Элементы GF(256), которые составляют подполе из 4-х элементов, это {0,1, ⁸⁵, ¹⁷⁰}. Сопряженные относительно поля GF(2) элементы:

,², ⁴, ⁸, ¹⁶, ³², ¹²⁸.

Сопряженные относительно поля GF(4) элементы, которые нас интересуют:

, ⁴,¹⁶,⁶⁴.

Следовательно,

g(x)=(x-)(x-⁴) (x-¹⁶) (x-⁶⁴)= (x-³) (x-¹²) (x-⁴⁸) (x-¹⁹²)

Раскрыв скобки гарантируем, что получим многочлен с коэффициентами из GF(4). Вычисления естественно длинные. Ответ

g(x) =x⁴ + x³ + ¹⁷⁰ x+1 или g(x)= x⁴ + x³ +3x+1, или (85,81) код Хэмминга над GF(4).

Аналогичный подход можно применить для построения сверточных кодов, способных исправлять двойные ошибки. Для этого используется двоичный код БЧХ примитивной длины с d=6. Для произвольного m3. Это код (n,k) (2^m-1, 2^m-2-2m). Его проверочная матрица

H - двоичная матрица размерности mx(2^m-1), 1 - вектор строка из 1 длины 2^m-1. Сверточный код (n,k)будет задаваться проверочной матрицей:

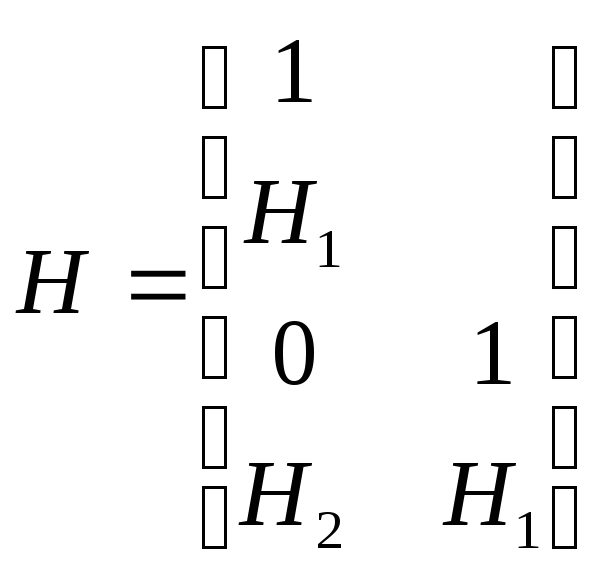0 - строка из 2^m-1 нулей.

Задача.

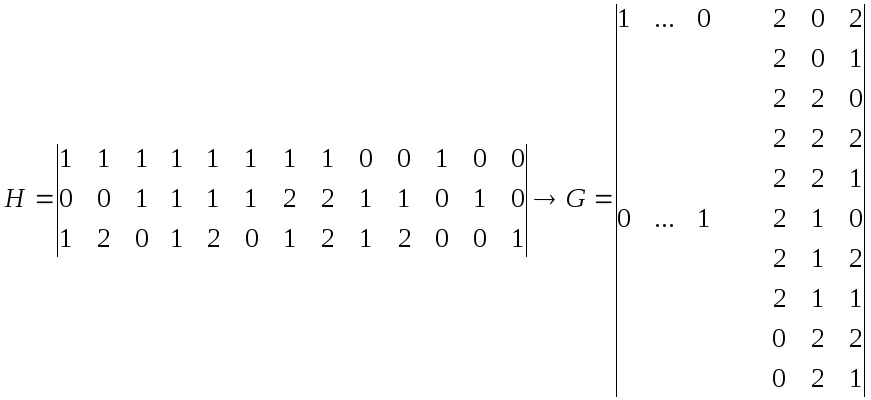
1. Построить проверочную матрицу систематического восьмиричного (9, 7) – кода Хэмминга.

2. Основываясь на этом коде найти проверочную матрицу (30, 27) – кода Вайнера-Эша над GF(8).

3. Построить кодер и синдромный декодер.

4. Чему равно скорость этого кода?