Минимизация функционала качества четырехмерной вариационной ассимиляции

Если представить функционал качества в виде суммы элементов, где индексы соответствуют модельной сетке, а- станциям наблюдений

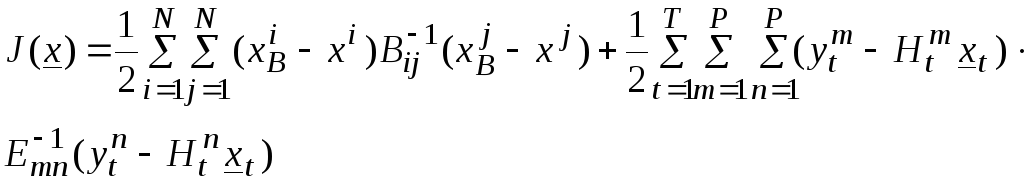
Где - число узлов модельной сетки,- число временных интервалов в течение окна ассимиляции,- число станций измерений.

Вычисляем градиент по отношению к элементу вектора состояния среды :

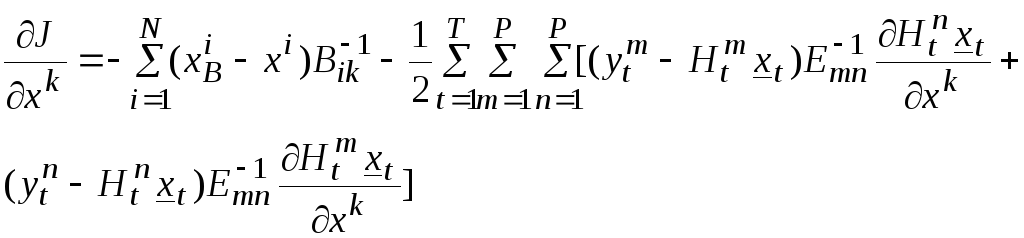или с учетом равнозначности сумм во втором слагаемом

Если обобщить для всех элементов вектора состояния среды и записать в матричном виде:

Выраженные в Якобиане чувствительности вычисляются относительно начальных значений в модели, тогда как модель оперирует с моментом времени, на который вычисляются моделируемые характеристики. Соответственно, более естественный Якобиан должен выглядеть как

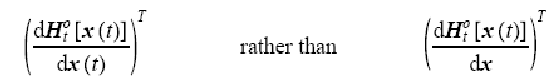
Где левая честь относится к тому же моменту времени, что и наблюдения. Если взять дифференциал от уравнения модели, то получим

Откуда дифференцирование элементов Якобиана с учетом действия модели

Где элементы матрицы представляют собой.

Подставляя в уравнение для градиента, получаем

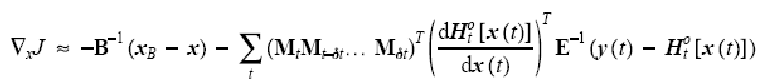
В этом уравнении мы линеаризовали сопряженный оператор модели (прямые буквы оператора модели в отличие от наклонных, означающих изначально нелинейный оператор модели). В этом смысле эти операторы представляют собой операторы прогноза возмущений. С учетом того, что производная фактически представляет собой линеаризацию оператора наблюдений. Тогда аналогично оператору модели, можно обозначить прямыми буквами линеаризованный оператор наблюдений

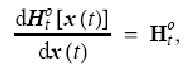
В отличие от, в общем случае, нелинейного исходного оператора наблюдений, обозначенного наклонной буквой (под знаком производной). Тогда выражение для градиента будет выглядеть как

Где к последовательности сопряженных операторов временной эволюции, описываемой оператором модели, также применена операция транспонирования по отдельности к каждому из последовательности.

Оценка градиента функционала качества

Оценка градиента по отношению к варьированию начальных условий может осуществляться одним из трех способов:

1. Непосредственно вычислить градиент как конечные разности функционала качества

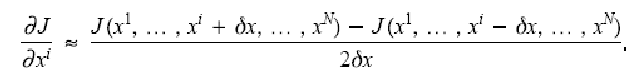
Как, например, в этой формуле центральных разностей градиента для каждой метеовеличины в каждом узле модельной сетки. Этот способ на практике требует вычислений градиента. С учетом того, что в стандартной модели прогноза погодыили более, этот метод будет вычислительно затратный.

2. Вычислять градиент по только что полученной формуле. Это будет означать, что на каждом шаге надо будет применять к последовательность, что также приводит к большому количеству повторяющихся вычислений.

3. Использовать метод сопряженных операторов, позволяющий оперировать не с матрицами, а с операторами.

Где

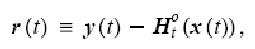
С учетом того, что градиент функционала качества может быть представлен в виде:

последовательность операций может быть сформулирована как следующая:

1. Выполняем интегрирование модели от до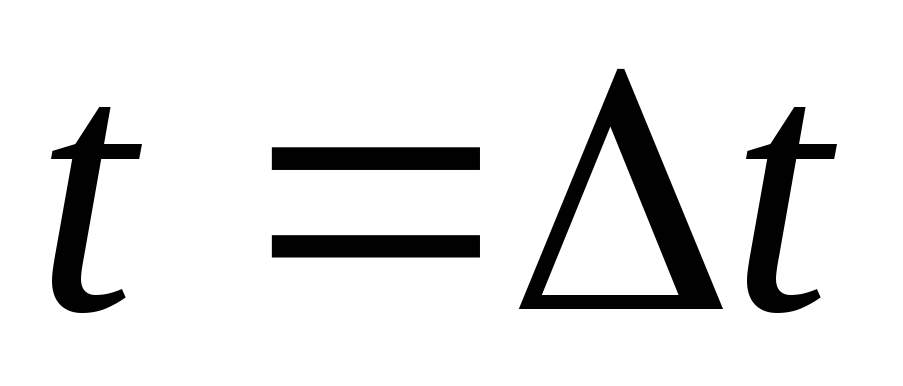, используя прямую и нелинейную версию модели. В качестве начальных условий используется первое приближение, т.е. результат моделирования с предыдущего шага. На каждом временном шагесохраняем значения;

2. Для момента времени вычисляем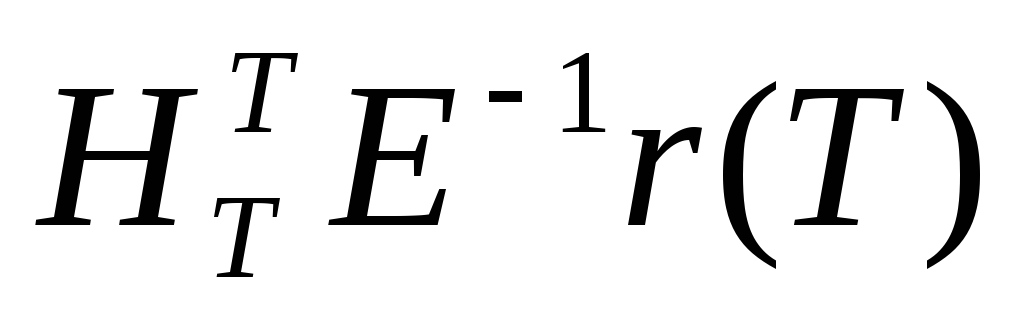, что соответствует правому верхнему углу приведенной таблицы. Обозначаем этот результат как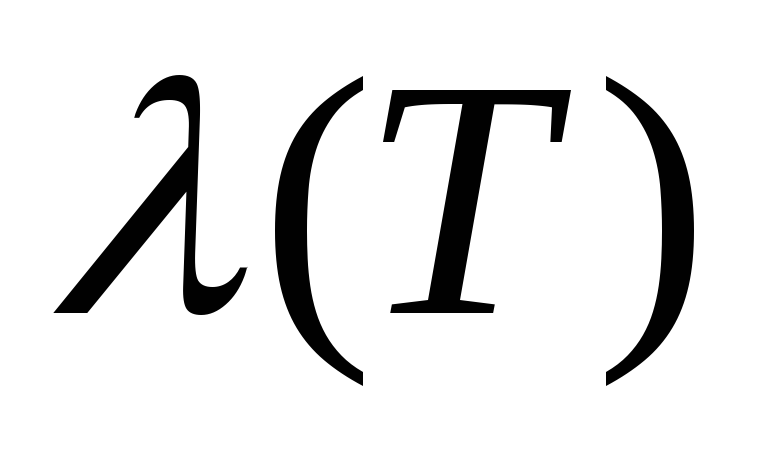- это будет вектор сопряженных переменных.

3. Интегрируем сопряженную переменную обратно по времени на 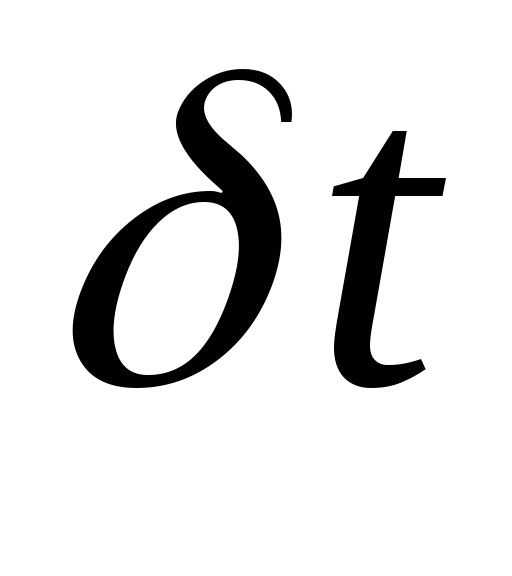. Для этого заменяемна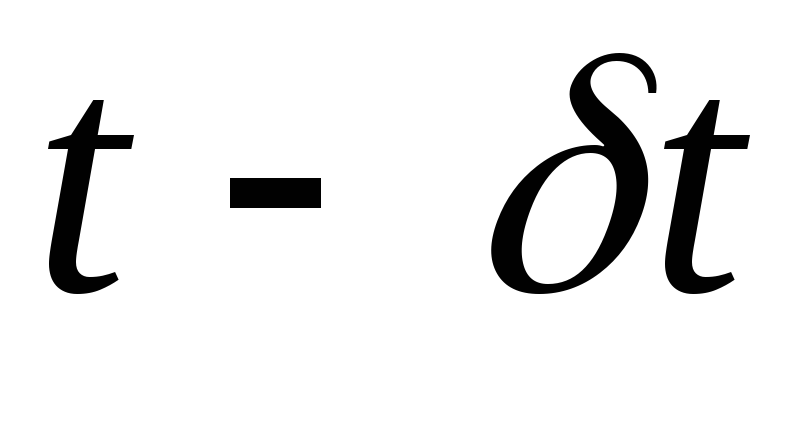и вычисляем вектор сопряженных переменных на этом шаге через сопряженные переменные на следующем шаге, полученные в п.2.

При этом используется информация о , полученная при прямом интегрировании модели. В приведенной таблице это соответствует переходу из правого верхнего угла вниз и налево.

4. Переходим еще на один шаг обратно во времени и повторяем пункт 3, пока не доходим до 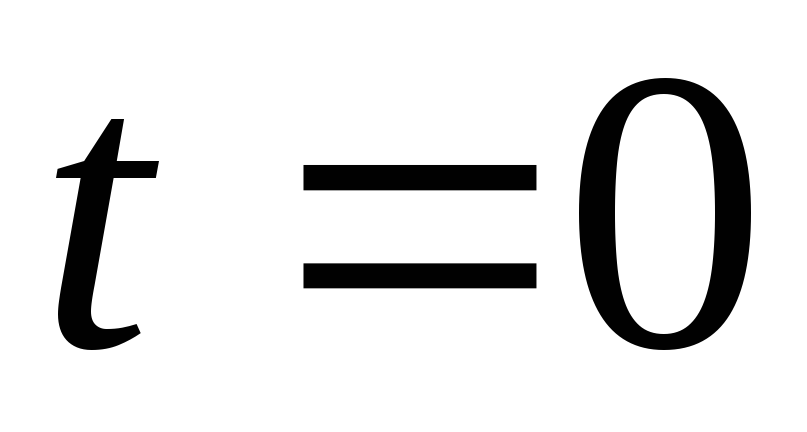. Для этого момента времени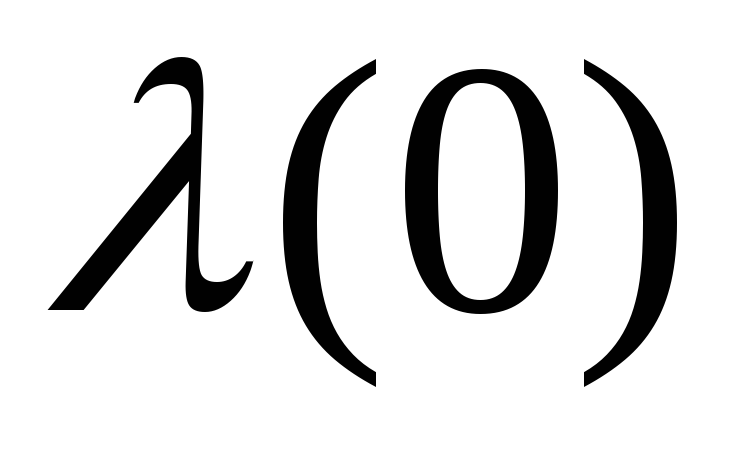представляет собой минус градиент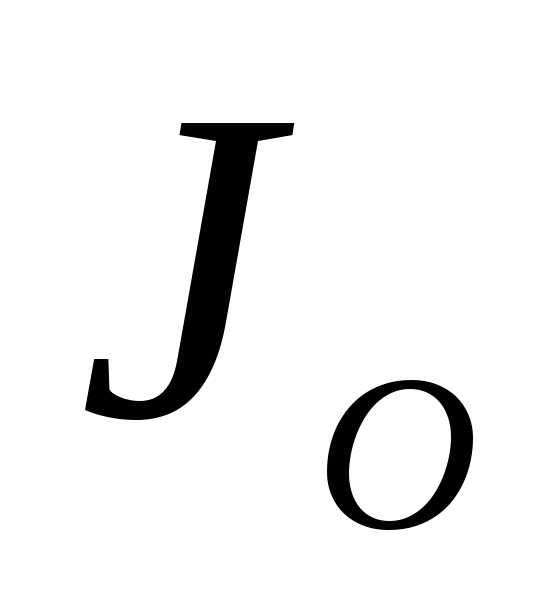по отношению к.

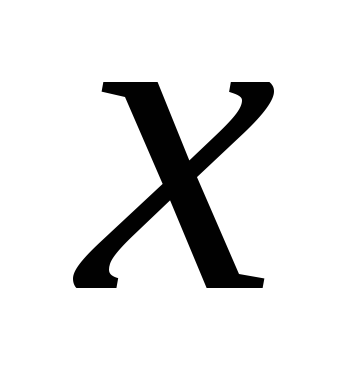5. Вычисляем полный градиент, добавляя слагаемое соответствующее минимизации расхождения анализа и моделирования

Примененный в таком виде данный метод имеет три стадии (рисунок 3):

1. Интегрирование прямой модели (шаг 1);

2. Обратное интегрирование сопряженных переменных (шаги 2-4);

3. Добавление модельного вклада и вычисление новых начальных условий.

Оптимальное состояние достигается когда , что означает, что функционал качества достигает минимума.

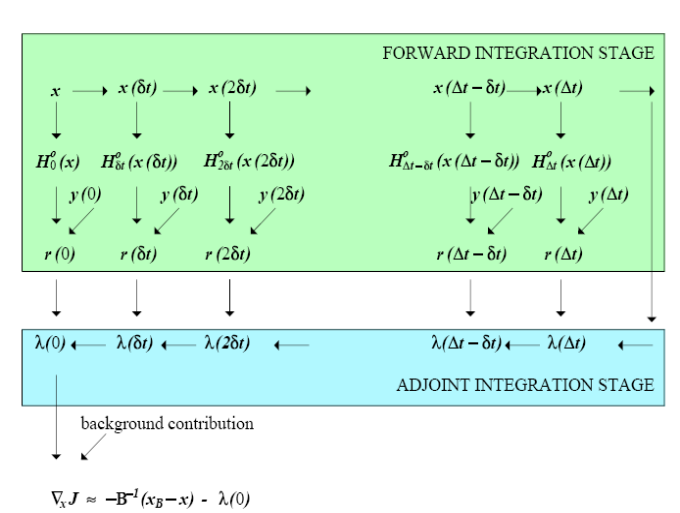
Рисунок 3. Иллюстрация метода сопряженных переменных.