Функционал качества четырехмерной вариационной ассимиляции

Используемый в вариационном анализе подход заключается в поиске таких начальных условий для модели, которые приводят к минимизации некой скалярной величины, называемой функционалом качества.представляет собой глобальную меру одновременного расхождения, представляющего собой текущую оценку истинного состояния среды (метеорологических параметров), и двух независимых представлений этой среды. Первое из этих представлений получается по результатам измерений, а второе – по результатам моделирования. Последние измерения (в пределах окна ассимиляции) образуют вектор измерений- первое представление. Второе представление образует вектор фонового состояния, относящийся к моменту времени.

Традиционная форма функционала качества, как и в трехмерном вариационном анализе

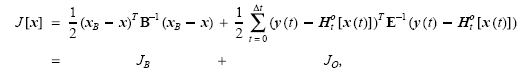
Первая часть функционала качества, соответствующая минимизации расхождения с модельными расчетами такая же, как в трехмерном вариационном анализе. Во второй части, соответствующей минимизации расхождения результатов анализа с наблюдениями, появилась зависимость от времени. Для учета изменчивости анализируемой метеорологической величины во времени используется модельный оператор

действующий последовательно от момента времени до момента временис шагами. Следующий рисунок иллюстрирует последовательность решения прямой задачи с использованием модели.

Оператор модели используется для расчета эволюции анализируемой величины во времени, тогда как оператор наблюденийприменяется для каждого состояния модели во времени для предсказания аналога наблюдений, соответствующего данному моменту времени, в точке пространства, где фактически находится станция наблюдений в тех единицах, в которых это наблюдение производится. В результате действия этих операторов формируется модельное представление наблюдений, соответствующее каждому моменту времени. Эти значения затем сравниваются с фактическими наблюдениями.

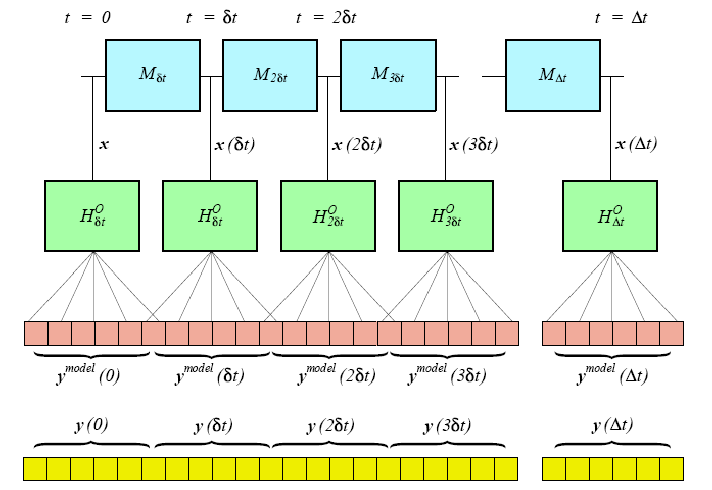
Рисунок 2. Иллюстрация решения прямой задачи.

Математически действие операторов моделирования и наблюдений выражается как

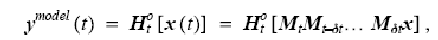
что означает, что модельный образ наблюдений в момент времени формируется в результате последовательного воздействия модельного оператора, начиная от начального состояния.

Как модельный оператор, так и оператор наблюдений в общем случае являются нелинейными, хотя оператор наблюдений часто представляет собой простую линейную интерполяцию из узлов модельной сетки в точки, где производятся наблюдения.

Ошибки наблюдений представляются матрицей , на диагонали которой стоят собственно дисперсии ошибок, а вне диагонали ковариации ошибок в разных точках наблюдений. Т.к. наблюдения обычно не коррелируют друг с другом, эта матрица сводится к диагональной, которую легко можно обратить. Однако часто наблюдения подвергаются препроцессингу, т.е. предварительной обработке, в результате чего они могут коррелировать друг с другом.

Необходимость нахождения начальных условий может быть сформулирована как задача нахожденияэлементов, которые минимизируют функционал. Для минимизации функционала можно использовать метод наискорейшего спуска. Для начала этого процесса в качестве первого приближения можно использовать. Для осуществления алгоритма спуска необязательно вычислять значение самого функционала, хотя это делать полезно с диагностической целью, а нужно вычислять градиент

Который используется для определения как нужно модифицировать , чтобы уменьшить значение. В минимуместационарен, когда. Градиент представляет собой вектор размерности, каждый элемент которого