Лабораторная работа №11. Изучение робастных оценок наклона линии регрессии

Пусть надежно установлено, что имеется функциональная зависимость между двумя группами числовых переменных представленными в виде пар чисел (x_i,y_i), где y_i - значение отклика при заданном значении фактора x_i. Пару значений (x_i,y_i) называют результатом одного измерения, a n - числом измерений. Предполагаем, что наблюдаемое в опыте значение отклика у можно мысленно разделить на две части. Одна из них закономерно зависит от х, другая часть - случайна по отношению к х:

у = ƒ(х) + ε.

Случайное слагаемое ε выражает либо внутренне присущую отклику изменчивость, либо влияние на него не учтенных факторов. Иногда ε называют ошибкой эксперимента, связывая её присутствие с несовершенством метода измерения у. Разделение у на закономерную и случайную составляющие можно сделать только мысленно. Реально ни f(х_j), ни ε_j в отдельности не известны, в опыте узнаем только их сумму. Предположения относительно величин в классической модели регрессионного анализа:

• все опыты были проведены независимо друг от друга в том смысле, что случайности, вызвавшие отклонение отклика от закономерности в одном опыте, не оказывали влияния на подобные отклонения в других опытах;

• статистическая природа этих случайных составляющих оставалась неизменной во всех опытах.

Из этих предположений вытекает, что случайные величины ε_j статистически независимы и одинаково распределены. Для того, чтобы задача о подборе функции отклика была осмысленной, необходимо определить набор допустимых функций f(х). Как правило, предполагают, что множество допустимых функций является параметрическим семейством f(х, θ). Тогда восстановление зависимости между х и у оказывается эквивалентным указанию значения оценки θ по исходным данным (x_i,y_i). Знание θ позволит по заданному значению фактора х предсказывать закономерную часть отклика у. Ситуация, в которой экспериментатор может выбирать значения факторов x_i по своему желанию и таким образом планировать будущие эксперименты, называется активным экспериментом. В этом случае значения факторов обычно рассматриваются как неслучайные. Сообразуясь с целями эксперимента, экспериментатор может выбрать его план (значения x_i) наилучшим образом. В отличие от этой ситуации в пассивном эксперименте значения фактора складываются вне воли экспериментатора под действием обстоятельств. Математическая обработка совокупности (x_i,y_i) от этого не меняется. Самый простой случай подобных задач - это исследование связи между одной независимой переменной х и одной зависимой переменной (откликом) у. Эта задача носит название простой регрессии. Исходными данными этой задачи является совокупность (x_i,y_i). Первым шагом решения задачи является предположение о возможном виде функциональной связи. Примерами таких предположений могут являться зависимости:

у = a + bx, у = a + bx + сх², у = e^a+bx, у = ln(a + bx),

где а, b, с - неизвестные параметры, которые надо определить по исходным данным. Для подбора вида зависимости строят график точек (x_i,y_i), называемый "облако рассеяния". Его вид подсказывает вероятную функцию. После подбора регрессионной модели и нахождения её параметров, выясняют, насколько хорошо модель описывает имеющиеся данные. Для этого изучают разности между наблюдаемыми и предсказанными значениями у, так называемые остатки. Согласно общим предположениям регрессионного анализа, остатки должны вести себя как независимые одинаково распределенные случайные величины. Исследование остатков начинают с изучения графиков их зависимости от номера наблюдения, зависимой и независимой переменных. Они могут показать наличие какой-то зависимости, не учтенной в модели. Скажем, при подборе простой линейной зависимости между х и у график остатков может показать необходимость перехода к нелинейной модели или включения в модель периодических компонент. График остатков показывает резко отклоняющиеся от модели наблюдения - выбросы. Подобным наблюдениям уделяют особое внимание, так как их присутствие может грубо искажать значения оценок. Устранение выбросов может проводиться с помощью удаления этих данных из совокупности. Эта процедура называется цензурированием. Можно применять робастные методы оценивания параметров, устойчивые к грубым отклонениям. В простейшем случае задача регрессионного анализа предполагает установление линейной зависимости:

y_i = A + bx_i + ε_i.

Здесь x_i - заданные числа (значения фактора); y_i - наблюденные значения отклика; ε_i - независимые (ненаблюдаемые) одинаково распределенные случайные величины. Считаем, что нет оснований предполагать какой-либо закон распределения случайных величин ε, однако можно считать, что ε_i распределены непрерывно. Выводы о зависимости между у и х будем основывать на рангах у. Ясно, что в таком случае ничего определенного о величине А сказать не удается, так как изменение всех y_i на одну и ту же постоянную величину не изменяет рангов y_i. Задача свелась к поиску единственного неизвестного коэффициента наклона b. Нумеруем наблюдения так, чтобы иксы возрастали с ростом номера. Если из наблюденных величин yi вычесть истинные значения bх_i то остатки y_i - bx_i = А + ε_i образуют последовательность независимых одинаково распределённых случайных величин. Не зная b, будем вычитать из y_i переменную величину βx_i, где β изменяется по нашему произволу. Тенденцию изменения значений с измене-нием номера или её отсутствие можно обнаружить с помощью коэффициентов корреляции. Выборочный коэффициент корреляции Пирсона по совокупности (x_i, y_i - x_i) имеет вид:

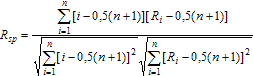
Наименьшей зависимости остатков соответствует r = 0. Для неизвестного β это дает уравнение:

Его решение - это известное выражение оценки наименьших квадратов. Составим коэффициент ранговой корреляции Спирмена. Он получается заменой величин y_i - bx_i и x_i в коэффициенте выборочной корреляции Пирсона на их ранги. Упорядочим x_i. Тогда ранг x_i равен i (при условии отсутствия совпадений между x_i). Таким образом:

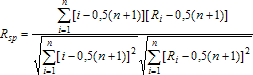
где R_i - ранг величины y_i - bx_i. Поскольку R_i принимает значения от 1 до n, то оба корня в знаменателе равны n(n² - 1)/12. Преобразовав числитель, находим:

Коэффициент корреляции Кендэла определяется как , где Р и Q - соответственно число согласованных и несогласованных пар (y_i - bx_i, x_i) и (y_j - bx_j, x_j) для всех i, j таких, что i < j. Здесь пары (y_i - bx_i, x_i) и (y_j - bx_j, x_j) называются согласованными, если оба значения одной пары больше обоих значений другой. В противном случае пары называются несогласованными. Величина K = Р - Q называется статистикой Кендэла. Ее можно записать в следующем виде: . Измеренная с помощью этих коэффициентов ранговой корреляции зависимость между рядами (y_i - βx_i) и x_j будет наименьшей, если выбрать β так, чтобы τ и R_sp были равны нулю. Проанализируем упрощённо зависимость τ(β). При β < 0 и очень больших по абсолютной величине, порядок следования разностей (y_i - βx_i) определяется исключительно числами xi, то есть τ = 1. Пусть теперь начинает возрастать. Первое изменение порядка следования произойдет при первом совпадении: y_i - βx_i = y_j - βx_j . При этом Р и Q изменятся на 1 каждый, уменьшится на 4/n(n - 1). При дальнейшем увеличении β такие изменения будут происходить всякий раз, как будет достигаться равенство в парах y_i - βx_i = y_j - βx_j, то есть при таких значениях β = β_ij:

если все числа x_i различны между собой. Иначе используем лишь такие i, j для которых x_i ≠ x_j. Точек изменения коэффициентов оказывается в этом случае меньше, чем число сочетаний С_n², но величины скачков могут быть больше. Симметрично расположенные скачки равны по величине, поэтому график τ(β) проходит через ноль при таком β₀, что левее и правее него остаются по одинаковому количеству точек разрыва. Иначе говоря:

Это оценка коэффициента наклона. В условиях гауссовской модели она менее точна, чем стандартная, но зато она применима в гораздо более широких условиях. Строим доверительные интервалы для неизвестного b. Пусть коэффициент доверия 1 - 2ε. Пусть τ_ε для данного n обозначает верхнее критическое значение коэффициента τ. Точки скачков функции τ(β) выделяют доверительный интервал β: |τ(β)| ≤ τ_ε. Статистика Кендэлла K, введем функцию Это оценка коэффициента наклона. Можно показать, что в условиях гауссовской модели она менее точна, чем стандартная, но зато она применима в гораздо более широких условиях. Основываясь на характере функций, можно построить доверительные интервалы для неизвестного b. Выберем коэффициент доверия 1 - 2а. Пусть для данного n τа обозначает верхнее критическое значение для коэффициента ранговой корреляции τ. Точки скачков функции τ(β) выделяют доверительный интервал: β: |τ(β)| ≤ τ_a. Учитывая, что таблицы распределения чаще составлены не для величины τ_a, а для статистики Кендэла K, введем функцию . Скачки этой функции равны 2. Доверительный интервал для b с коэффициентом доверия 1 - 2ε имеет вид: |K(β)| ≤ K_ε, где K_ε есть решение уравнения:

Р{|K| ≤ K_ε} = 1 - 2ε Р{K ≥ K_ε + 2} = 0,5ε.

Обозначим вариационный ряд β_ij через S. Если среди х_i нет совпадающих, то количество чисел β_ij равно N = 0,5n(n - 1). Положим M₁ = (N - K_а)/2, M₂ = (N + K_а)/2. Тогда доверительный интервал для b имеет вид:

{S_M¹ ≤ b ≤ S_{M² + 1}}, P{ S_M¹ ≤ b ≤ S_{M² + 1}} = 1 - ε.

В случае больших n для K используется приближенное выражение, основанное на нормальной аппроксимации распределения K при гипотезе независимости: , где z - обычный квантиль нормального распределения. Известна методика учёта поправок при совпадениях час

Вопросы для самопроверки

В чём отличие группированного статистического ряда от упорядоченной статистической совокупности

В чём отличие частоты от вероятности

Вопросы к экзаменам

1.Первичная статистическая совокупность, её упорядочение

2. Статистическая функция распределения.

3. Группированный статистический ряд.

4. Гистограмма.

5. Выравнивание статистических распределений.

Именной указатель

Перечень сокращений

9