Возвращение к примеру

Вернемся к нашему примеру и покажем, что четвертое взвешивание вовсе не было напрасным. Попробуем извлечь из него полезную информацию. Построим линейную модель, соответствующую этому опыту. Обозначим через истинный суммарный вес трех образцов. Теперь можем записать

Согласно сказанному выше, для того чтобы найти оценку неизвестных параметров следует минимизировать по функцию

Оказывается, что минимум достигается в точке , где

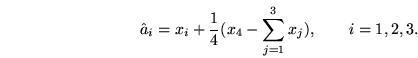
Упражнение 7.1

Сравнить ив предыдущем примере. Вспомнить содержание6.5и сделать вывод.

Пример 7.1

Независимая выборка из нормального распределения (Примеры 6.1и6.3) можно считать частным случаем линейной модели (37), если выбрать следующее подпространство:

Так как это подпространство одномерно, то имеет виддля некоторого, которое может быть найдено из условия ортогональности:

Приравнивая к нулю скалярное произведение этих векторов, получим

откуда , следовательно,. Этот результат полезно сравнить с оценкой математического ожидания, полученной в Примере6.10.

Замечание 7.1

Мы не коснулись здесь вопроса о том, как оценить дисперсию погрешности прибора в модели (37) в том случае, когда она является неизвестной. Подробное обсуждение этого вопроса можно найти в книге [12, Гл. 3, § 3]

След.:7.2 Система нормальных уравнений ...Пред.:7 Метод наименьших квадратов ...Вверх:7 Метод наименьших квадратов ...

ОглавлениеПредметный указатель

7.2 Система нормальных уравнений

Существует следующая модификация линейной модели. Пусть -- вектор-столбец неизвестных параметров. Предположим, что мы не можем непосредственно наблюдать, но можем измерить их некоторые линейные комбинации прибором, допускающим независимые случайные ошибки. Сформулируем точную модель. Пусть---матрица,-- вектор-столбец результатов измерений,-- вектор-столбец ошибок,--. Основное предположение состоит в том, чтои

Рассмотрим подпространство в , порожденное столбцами матрицы:

Если ввести новые параметры 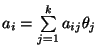, то задача сведется к виду (37). Согласно7.1оценкадолжна быть найдена из условия

следовательно, . Это равносильно тому, чтодля любого, то есть, где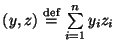. Пользуясь свойствами скалярного произведения, получим

Отсюда вытекает, что

(39)

Таким образом, может быть найдено из системы линейных уравнений (39), именуемойсистемой нормальных уравнений. Если матрицаимеет полный ранг, то квадратная матрицаобратима и

7.3 Регрессионная модель и задача о сглаживании наблюдений

В настоящем параграфе под данными мы будем понимать набор из пар чисел:

(40)

причем пара представляет собой исход единичного наблюдения. Роль чиселив паре является различной и состоит в следующем. Предполагается, что экспериментатор может абсолютно точно задавать во время опыта значенияи затем измерять, допуская при этом случайную ошибку, значение. Например,-- температура, выбираемая в процессе эксперимента над образцом материала,-- длина образца при соответствующей температуре. Числопринято называтьфактором, а число--откликом. Экспериментатор предполагает, что между величинамиисуществует функциональная зависимость вида

где известные функции, а-- неизвестные параметры. Предполагая, что ошибки, связанные с измерением отклика, независимы и имеют распределение, получим следующую модель

Она называетсярегрессионной моделью. Задача состоит в том, чтобы оценить неизвестные величиныпо данным наблюдений (40).

Для решения этой задачи эффективным оказывается подход, применяемый в предыдущих параграфах: хорошей оценкой неизвестных параметров является та, которая ``минимизирует сумму квадратов'':

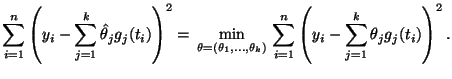
Много дополнительных сведений о свойствах оценок наименьших квадратов в модели регрессионного анализа, о проверке предпосылок к применению этой модели, а также о проверке ее адекватности, можно почерпнуть из книги [13].

Иногда в качестве берут степенные функции:

Таким образом, речь идет о том, чтобы приблизить неизвестную функциональную зависимостьотполиномом вида. В этом случае говорят озадаче сглаживания наблюденийпри помощи полинома. Более подробно об этой важной задаче, в том числе о проблеме выбора степени полинома, можно прочитать в книге [12].