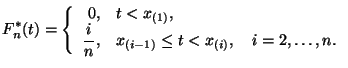5. Проверка нормальности при помощи вероятностной бумаги

Этот простой графический метод часто используют для первоначальной прикидки, правдоподобно ли предположение о том, что независимая выборка взята из нормального распределения. Эта прикидка осуществляется в буквальном смысле ``на глазок'', поэтому здесь не идет речь о количественных показателях, таких как вероятность ошибки и т.п.

Чтобы пояснить идею этого метода, сформулируем вспомогательное утверждение. Пусть -- функция распределения закона,.

Лемма 1. Рассмотрим отображение , действующее по формуле

где обозначает функцию, обратную к функции распределения стандартного нормального закона. При этом отображении графикпереходит в прямую линию, а графикпереходит в прямую линию.

Доказательство. Достаточно заметить, что. См. по этому поводу также Упражнение3.6на стр..

Предположим, что в нашей выборке все числа различны. Переупорядочим выборку в порядке возрастания:

То, что получается после такого переупорядочения, называют вариационным рядом.

Из Определения 6.1легко вытекает, что в этом случае эмпирическая функция распределения может быть выражена формулой

(54)

В частности, .

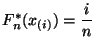С другой стороны, теорема Гливенко утверждает, что при большом объеме выборки эмпирическая функция распределения близка к теоретической функции распределения. Принимая во внимание Лемму 9.1, заключаем, что если выборкадействительно взята из нормального распределения, то точки

(55)

должны приблизительно оказаться на одной прямой линии (а именно, на прямой ).

Замечание 9.2  

Мы намеренно не включаем в перечень (55) точку, соответствующую, так как, а отображениев точках видане определено.

Таким образом, мы пришли к очень простому глазомерному способупроверки нормальности выборки: наносим на плоскость точки

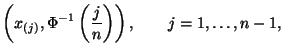
и смотрим, лежат ли они вблизи какой-либо прямой линии. Если такую прямую можно провести, то по ее чертежу можно грубо оценить значения неизвестных параметров и.

Чтобы было удобнее наносить эти точки, прибегают к так называемой вероятностной бумаге. Вероятностная бумага получается выбором неравномерной шкалы координат вдоль оси ординат. А именно, на расстоянииот оси абсцисс мы ставим пометкудля новой неравномерной шкалы. На вероятностную бумагу (в системе новых координат) наносят точки.

Замечание 9.3  

В силу того, что данные наблюдений и измерений, как правило, округлены до некоторого знака, предположение о том, что все различны, нередко нарушается. Это приводит к тому, что в вариационном ряду некоторые соседние значения могут совпадать и формула (54) для выражениячерез вариационный ряд несколько видоизменяется. Но, тем не менее, изложенный выше глазомерныйметодопределения нормальностиостается пригодным.

Замечание 9.4  

Мы не используем точку , тем самым теряя некоторую информацию, содержащуюся в выборке. Имея в виду приблизительность этого метода, можно надеяться, что в случае больших выборок, эта потеря не слишком существенна. Отметим, однако, что существуют приемы, позволяющие учитывать и значение. Нетрудно модифицировать этот метод для проверки гипотез о выборках из распределений, не являющих нормальными, но зависящих от неизвестных параметров сдвига-растяжения. Детали можно найти, например, в [13, § 5.1] и [6, § 4].

Пример 9.1  

Вернемся к нашему числовому Примеру 6.4и зададимся вопросом, насколько в Примере8.2было обоснованным предположение о нормальности выбороки. Для этого проведем их проверку на нормальность при помощи вероятностной бумаги.

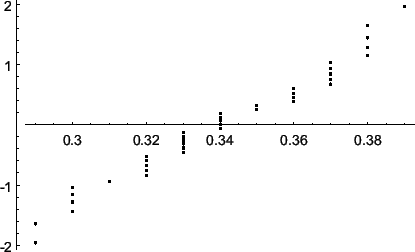
Для выборки , соответствующей содержанию углерода в пробах, чертеж представлен на рисунке3.

Рис. Данные о процентном содержании углерода в пробах

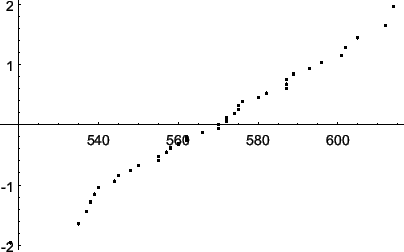
Для выборки , содержащей значения прочности на разрыв, чертеж представлен на рисунке4.

Рис. Данные о значениях прочности на разрыв

Видно, что и в том, и в другом случае точки располагаются вблизи некоторой прямой линии. Таким образом, имеются основания для гипотез о нормальности выборок и.

Большое число естественно-научных примеров, при анализе которых используется вероятностная бумага, содержится во второй части книги [12].