Лекция 4

Проверка статистических гипотез

Основные вопросы лекции:

1. Общая постановка задачи проверки гипотез.

2. Проверка гипотезы о равенстве центров распределений двух нормальных генеральных совокупностей при известном и неизвестном среднем квадратическом отклонении.

3. F – распределение.

4. Проверка гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей.

5. Проверка гипотез о законе распределения.

6. Критерий согласия Хи – квадрат.

Статистические гипотезы

Как отмечалось выше, в математической статистике считается, что данные, получаемые в результате наблюдений, подчинены некоторому неизвестному вероятностному распределению, и задача состоит в том, чтобы извлечь из данных правдоподобную информацию об этом неизвестном распределении. В настоящей главе мы обсудим еще один подход к этой общей задаче, состоящий в проверке гипотез. Статистической гипотезойназывают предположение о распределении вероятностей, которое необходимо проверить по имеющимся данным.

Параграфы этой главы:

1. Простые и сложные гипотезы и их проверка

Пусть -- независимая выборка, соответствующая неизвестной функции распределения.Простой гипотезойназывают предположение, состоящее в том, что неизвестная функцияотвечает некоторому совершенно конкретному вероятностному распределению. Пример простой гипотезы:

            : данные являются выборкой из равномерного распределения                     в отрезке .

Сложной гипотезойназывают предположение о том, что неизвестная функцияпринадлежит некоторому множеству распределений, состоящему из более чем одного элемента. В качестве иллюстрации можно привести Пример6.3.

Проверить статистическую гипотезу -- это значитна основе имеющихся данныхпринять или отвергнутьсделанное предположение. Для этого используется подход, основанный на выборе так называемогокритического множества. Мы поступаем следующим образом: если данные наблюденийпопадают в критическое множество(то есть,), то гипотезаотвергается; если же данные находятсявне критического множества(то есть,), то гипотезапринимается. Такое решающее правило будем называтькритерием, основанным на критическом множестве.

Существует много методов построения критических множеств для проверки статистических гипотез, некоторые из этих методов обсуждаются в последующих параграфах. Сейчас мы кратко коснемся вопроса о возможных ошибках, которые мы допускаем, принимая или отвергая гипотезы.

В силу случайной природы наблюдаемых данных возможна ситуация в то время, когда гипотезасправедлива. Однако, согласно решающему правилу, в этом случае мы отвергнем верную гипотезуи, тем самым, допустим ошибку. Очевидно, что в случае простой гипотезывероятность такой ошибки равна. Эту вероятность называют такжеуровнем значимостистатистического критерия. Такого рода ошибки неизбежны при анализе случайных данных, и их не следует драматизировать. На практике уровень значимости критерия задается изначально, исходя из реальных приложений и потенциальных последствий возможных ошибок.

2. Критерий согласия Пирсона

Наше изложение близко к [7, § 30.1] и [13, § 10.4]. Мы рассматриваем независимую выборку, обозначая неизвестную функцию распределения. Нас интересует вопрос о том, согласуются ли данные наблюденийс простой гипотезой

где -- некоторая конкретная фиксированная функция распределения.

Вначале разобъем множество на конечное число непересекающихся подмножеств. Пусть-- вероятность, соответствующая функции распределения, обозначимОчевидно, что

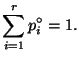
Теперь сделаем группировку данных аналогично процедуре, описанной в  6.3, а именно, определим

(50)

Очевидно, что в силу случайных колебаний эмпирические частоты будут отличаться от теоретических вероятностей. Чтобы контролировать это различие, следует подобрать хорошую меру расхождения между экспериментальными данными и гипотетическим теоретическим распределением. По аналогии с идеей метода наименьших квадратов в качестве такой меры расхождения можно взять, например,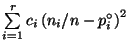, где положительные числаможно выбирать более или менее произвольно. Как показал К. Пирсон, если выбрать, то полученная величина будет обладать рядом замечательных свойств. Таким образом, положим

(51)

Подчеркнем, что величина вычисляется по выборке. Функциюпринято называтьстатистикой Пирсона. Обсудим ее свойства.