Лабораторная работа №13. Изучение методов оценки параметров распределений

В математической статистике различают две разновидности методов. Первую составляют методы оценивания параметров по конечной группе с фиксированным числом наблюдений, вторую - по неограниченно растущей группе, когда исследователь имеет возможность увеличивать число наблюдений. С теоретической точки зрения второй подход проще, так как при больших n исчезают многие проблемы, относящиеся к конечным группам. Основой для выводов в этом случае служит закон больших чисел - при больших n значения характеристик распределения группы приближаются к неизвестным теоретическим значениям этих характеристик. Теорема Чебышева дает способ оценки по группе данных теоретического значения математического ожидания: этой оценкой является среднее арифметическое значение наблюдений.

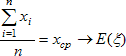
Ищем несмещённую оценку по группе данных для дисперсии распределения случайной величины. Пусть х₁,...,х_n - совокупность независимых реализаций случайной величины ξ, среднее значение которой равно а. Согласно закону больших чисел, для получения приближенного значения дисперсии Dξ = Е(ξ - Е(ξ))² надо в определении дисперсии заменить теоретическую функцию распределения F на ее аналог F_n. Иначе говоря, требуется заменить операцию нахождения математического ожидания Е усреднением по группе. Сначала сделаем это по отношению к Е, стоящему внутри скобок. Вместо (ξ - Е(ξ))² получим совокупность (х₁ - х_cp)², (х₂ - х_cp)²,..., (х_n - х_cp)². Ищем приближенное выражение для дисперсии:

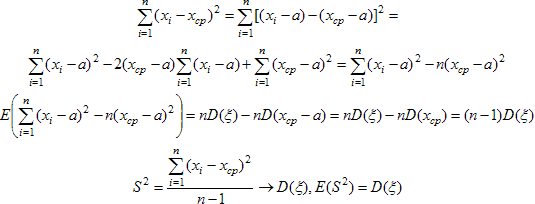
Поскольку среднее значение статистики S² равно дисперсии случайной величины, породившей группу наблюдений, то наблюдаемая величина S² является несмещенной оценкой для истинной дисперсии D(ξ). Пусть есть группа наблюдений случайной величины ξ с распределением, принадлежащим некоторому параметрическому семейству F(а). Необходимо по этим наблюдениям оценить неизвестный параметр а этого распределения. Для этого выберем какую-либо характеристику Т распределения случайной величины ξ, то есть среднее, медиану, квантиль, …, выражаемую через функцию распределения. Функция распределения F зависит от а. Значение характеристики Т также суть функция от неизвестного значения а. Наблюдаемый по группе аналог этой характеристики Т_n на основании закона больших чисел будет близок к ее теоретическому значению, если объем наблюдений достаточно велик. Поэтому решение уравнения:

Т(а) = Т_n

позволяет найти оценку одномерного параметра. Если параметров несколько, то выбираем несколько характеристик распределения и составляем систему из соответствующего количества уравнений. В качестве характеристик распределения обычно используют моменты или квантили. Соответственно, способы поиска оценок характеристик случайной величины называются "метод моментов" и "метод квантилей". Применим метод моментов для поиска параметров нормального закона. Пусть х₁,...,х_n - совокупность независимых реализаций случайной величины ξ, распределенной по нормальному закону N(a, σ²). Его плотность распределения . В качестве характеристик распределения будем использовать первый и второй моменты. Теоретические значения этих характеристик равны:

Приравнивая выборочные моменты к их теоретическим аналогам, получим: а = х_ср; 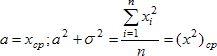. Получена оценка методом моментов, причём оценка среднего вновь среднее арифметическое, а оценка дисперсии отлична от найденной ранее несмещённой оценки. Биномиальное распределение задаётся единственным параметром р. Первый момент np = Σх_i = m, число успехов, оценка для р: р = m/n. Распределение Пуассона задаётся единственным параметром λ. Первый момент nλ = Σх_i, оценка для λ: λ = х_ср. Применим метод квантилей для поиска параметров нормального закона. Для нормального распределения и вообще для любого распределения, в котором параметрами служат сдвиг и масштаб, обычно используют медиану и квартили - верхнюю и нижнюю. Случайную величину ξ, распределенную по закону N(а₀, σ²), можно представить в виде ξ = а₀ + ησ, где η подчиняется распределению N(0,1) с плотностью . Для N(0,1) медиана равна 0, а нижняя и верхняя квартили равны ±Ф^-1(0,75) = ± 0,674. Здесь и далее под числом z = Ф^-1(b) подразумевается решение уравнения b = Ф(z), то есть:

Поэтому в общем случае для нормального закона N(а₀, σ²) медиана равна а₀, квартили равны: а₀ ± Ф^-1(0,75). В качестве оценки параметра распределения а можно использовать как медиану, так и половину суммы верхней и нижней квартилей распределения. Обозначим через med(хⁱ) медиану имеющейся совокупности данных, через Q(0,25) и Q(0,75) ее нижнюю и верхнюю квартили. Приравняв к теоретическим характеристикам их выборочные аналоги, получим следующие оценки:

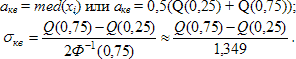
Поскольку для одних и тех же параметров распределения возможны и употребительны разные оценки, целесообразно выбирать из них те, которые лучше или которые обладают желательными свойствами. Состоятельность - практически обязательное свойство всех используемых на практике оценок, несмещенность лишь желательное. Многие часто применяемые оценки свойством несмещенности не обладают. Единого способа сравнения оценок не существует, приходится использовать различные подходы. Чаще всего в качестве критерия качества оценки a₀ параметра a выбирают малость величины среднего квадрата отклонения оценки от действительного значения Е(a₀ - а)², а наилучшей оценкой считают такую оценку, для которой эта величина минимальна. Более общий подход состоит в том, что выбирают неотрицательную функцию "штрафа" за отклонение a₀ от а (иногда говорят, функцию потерь), и наилучшей оценкой считают такую, для которой математическое ожидание величины штрафа минимально. Оценки, для которых минимальна некоторая функция потерь, часто называют оптимальными или эффективными. Но такие оценки не лучше других, так как оптимальные свойства оценок получены при определенных предположениях, которые на практике могут и не выполняться или выполняться лишь приближенно. При этом свойства подобных оценок могут оказаться не столь хорошими. Например, среднее арифметическое элементов выборки является "эффективной" оценкой математического ожидания. Для выборки из нормального распределения эта оценка несмещенная и обладает минимальной дисперсией. Но при отклонении распределения от нормального (например, при наличии "выбросов"), свойства этой оценки становятся неудовлетворительными. Во многих случаях представляет интерес не получение точечной оценки a₀ неизвестного параметра a, то есть одного числа, а указание области, интервала на числовой прямой, в которой этот параметр находится с вероятностью, не меньшей заданной (типично от 95% до 99%). Построить такую область можно следующим образом. Выберем число , близкое к единице: 0 < α < 1 - близкая к единице вероятность, с которой параметр a должен попасть в построенную область. Можно выбрать число ε, близкое к нулю 0 < ε < 1, как вероятность того, что параметр не попал в эту область. Ясно, что α + ε = 1. Пусть имеем точечную оценку a0 неизвестного параметра a и можем указать область А(a, ), в которую оценка a0 попадает с вероятностью не меньше α: P{a₀А(a, α)} ≥ α для любого a. Тогда доверительной областью (в одномерном случае - доверительным интервалом) с уровнем доверия α для неизвестного нам истинного значения a, построенной по наблюденному в опыте значению оценки a₀, является множество {a|a₀А(a, α)}. Процесс доверительного оценивания является как бы обращением процесса проверки статистических гипотез: там по известному значению параметра a строили множество А(a), в которое с заданной вероятностью попадает некоторая статистика a₀, а здесь по таким множествам строим область, которая накрывает с заданной вероятностью само значение a. Считается, что метод наибольшего правдоподобия позволяет оптимально использовать имеющейся в данных информацию о параметрах распределения случайной величины, породившей данные. Пусть х₁,...,х_n - данные, которые считаем реализациями случайной величины с распределением, плотность которого в точке х зависит от неизвестного параметра a. Обозначим плотность отдельного наблюдения х_i (i = 1,...,n) через р(x, a). Поскольку случайные величины х_i независимы, плотность вероятностей вектора (х₁,...,х_n) равна произведению плотностей с неизвестным истинным значением параметра. Подставим вместо переменных элементы наблюдений, то есть реализации случайных величин х₁,...,х_n, а параметр а будем рассматривать как переменную величину, изменяющуюся в заданной области значений. В таком случае найденная плотность превращается в величину, которую называют правдоподобием (likelihood): р(х₁, a) · р(х₂, a) · ... · р(х_n, a). Метод наибольшего правдоподобия рекомендует выбирать в качестве оценки a_l неизвестного истинного значения параметра а такое значение, при котором правдоподобие достигает максимума. Такой выбор происходит в зависимости от значений х₁,...,х_n, поэтому a_l является случайной величиной. Суть метода легче понять, анализируя следующую задачу. Требуется оценить число N рыб в пруду. Для этого из пруда выловили (случайным образом извлекли) M рыб, помечены и отпущены обратно в пруд. Через некоторое время, извлекли вторую группу n рыб и установили, что в этой группе m отмеченных. Считая, что пойманные в первый раз рыбы ко второму разу равномерно перемешались с непойманными, найти оценку максимального правдоподобия числа рыб в пруду, то есть наиболее вероятное при наблюдённых данных количество рыб в этом пруду. Решение: Количество способов извлечь случайным образом группу n рыб из N рыб, обитающих в пруду равно С_Nⁿ. Количество способов извлечь ровно m рыб из М отмеченных равно С_M^m. Количество способов извлечь ровно n - m рыб из N - M неотмеченных равно С_N-М^n-m. Два последних события независимы, поэтому число способов извлечь случайным образом именно ту группу, которая была извлечена, равно произведению найденных количеств, а вероятность извлечь её равна: . Для поиска максимума этой величины, найдём отношение. Это выражение равно единице при N = Mn/m - 1. При меньших N оно больше единицы, то есть вероятность растёт по мере роста N. При больших N оно меньше единицы, то есть убывает с ростом N. Значит, при целом искомая вероятность максимальная. Это и есть оценка методом правдоподобия для искомой величины N. Выполним оценку методом правдоподобия параметров нормальной модели N(a,b). Для неё функция правдоподобия равна:

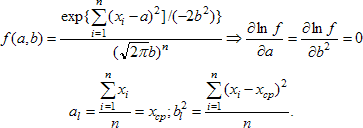
Оценки, полученные методом наибольшего правдоподобия и методом моментов, для нормального распределения совпали, но оценка дисперсии вновь отлична от найденной ранее несмещённой оценки дисперсии. Во многих случаях представляет интерес не получение точечной оценки a₀ неизвестного параметра a, одного числа, а указание интервала на числовой прямой, в которой этот параметр находится с вероятностью, не меньшей заданной (типично от 95% до 99%). Построить его можно следую-щим образом. Выберем вероятность α, близкую к единице, с которой параметр a должен попасть в построенную область (или ε, близкое к нулю 0 < ε < 1, как вероятность того, что параметр не попал в эту область, α + ε = 1). Пусть имеем точечную оценку a₀ параметра a и можем указать область А(a, α), в которую оценка a₀ попадает с вероятностью не меньше α: P{a₀А(a, α)} ≥ α для любого a. Тогда доверительным интервалом с уровнем доверия α для неизвестного нам истинного значения a, построенной по наблюденному в опыте значению оценки a₀, является множество {a|a₀А(a, α)}. Процесс доверительного оценивания является обращением процесса проверки статистических гипотез: там по известному значению параметра a строили множество А(a), в которое с заданной вероятностью попадает некоторая статистика a₀, а здесь по таким множествам строим область, которая накрывает с заданной вероятностью само значение a. В лабораторной работе решаются две не связанных между собой задачи:

• найти распределение реальных данных (страховых выплат некоторой фирмы)

• найти распределение модельной группы данных - смеси двух нормальных распределений.

Задача 1 Априорно известно, что обычно реальные выплаты страховой компании клиентам описываются такими распределениями, как Парето, Вейбулла или логнормальное. Предположим, что наблюдаемые страховые выплаты описываются распределением Парето:

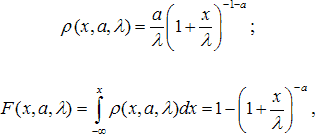
где все параметры и переменная положительны. Моменты этого распределения:

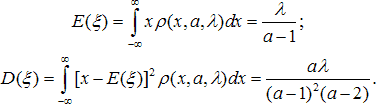
Первый момент определён при a > 1, второй - при a > 2. Несмещённые оценки среднего и дисперсии по наблюдаемым данным:

Формально приравнивая моменты, получаем систему двух уравнений метода моментов, имеющую единственное решение a = 2,475; λ = 4410. Полученное значение удовлетворяет требованию a > 2, однако оно может быть и формальным решением, не соответствующим сути явления, если истинное a < 2. Строим функцию правдоподобия:

Находим частные производные по a и по λ. Приравнивая производные нулю, получаем:

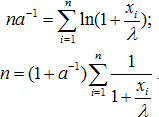
Система решалась с помощью Windows-приложения Maple - 9. Получены значения a = 1,909; λ = 2704. Видно, сколь значительно отличие результатов двух методов. Ясно и объяснение этого факта - найденное значение a меньше двух, то есть метод моментов является принципиально не применимым. Для проверки по критерию согласия Колмогорова-Смирнова преобразуем ряд данных в вариационный ряд и вычисляем статистику

D_n = max|F(x_i) - k/n| и |F(x_i) - (k - 1)/n|.

При соответствующем параметре и при справедливости нулевой гипотезы вероятность, что параметр Z равен наблюдаемому значению или превышает его, равна:

В случае, если a = 2,475 и λ = 4410 вероятность по Колмогорову 0,62, а для a = 1,909; λ = 2704 вероятность 0,92, то есть второе заметно вероятнее. График функции распределения экспериментальных данных и теоретического распределения Парето дан на рисунке 1. Видно хорошее сходство. Попытки улучшить сходство за счет подбора параметров при прямой проверке критерия Колмогорова-Смирнова не привела к успеху. В ходе этой попытки варьировались значения параметров распределения и вычислялось значение Z(a; λ). Установлено, что минимум этого выражения отличается от найденного значения не более, чем на 1%, то есть для использованных данных оценка прямой минимизацией функционала Z(a; ) не значительно отлична от оценки наибольшего правдоподобия.

Имеются данные, про которые предполагается, что они принадлежат смеси двух нормальных распределений. Необходимо найти параметры этих распределений и соотношение между ними. Расщепление провести методом моментов. Случайная величина, представляющей собой смесь двух нормальных распределений, задается пятью параметрами:

• р - доля первого распределения, р + q = 1;

• а₁, D₁ - математическое ожидание и дисперсия первого распределения;

• а₂, D₂ - математическое ожидание и дисперсия первого распределения.

Выразим через эти пять параметров теоретические характеристики смешанного распределения:

Ех = pа₁ + qа₂ D = pD₁ + q D₂ + pq(a₁ - а₂)²; M₃₀ = 3pq(a₁ - а₂)(D₂ - D₁) - pq(p - q)(a₁ - а₂)³; M₄₀ = 3pD₁² + 3qD₂² + pq(a₁ - а₂)²[(1 - 3pq)(a₁ - а₂)² + 6pD₂ + 6qD₁];

Задача свелась к решению системы четырёх уравнений с пятью неизвестными. Для замыкания использовали теоретическое соотношение для верхней квартили. Последнее уравнение решалось графически. В работе были генерированы две последовательности. Первая из 50 чисел с распределением N(3,1), вторая из 150 чисел с распределением N(6,1). При этом р = 0,25. Расчёт велся пошагово и последнее значение найдено по графику зависимости значения верхней квартили от р. Найдено:

a2 - a1 = a21 := 3.100156536 d2 := 1.084833215 d1 := 0.8685383266 a1 := 2.850792779 a2 := 5.950949315

Полученные результаты близки к заложенным. Теоретическая функция распределения и эмпирическая функция реальных данных построены на графике. Они явно близки. Проверка по критерию Колмогорова (асимптотическое соотношение для статистики D_n) даёт формальную вероятность совпадения зависимостей 97%, то есть совпадение следует считать хорошим.

29