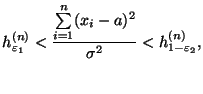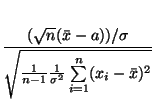Доверительный интервал для дисперсии при известном среднем

Здесь среднее считается известным фиксированным числом, а дисперсиявыступает в роли неизвестного параметра. Положим

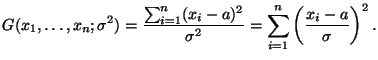
Так как --, тоимеет стандартное нормальное распределение. Тем самым, функцияимеет-распределение сстепенями свободы, никаким образом не зависящее от неизвестного параметра. Обозначая черезквантили этого распределения и фиксируя некоторые, такие, что, приходим к неравенству

(47)

которое выполнено с вероятностью . Откуда получаем-доверительный интервал для:

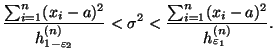
Доверительный интервал для дисперсии при неизвестном среднем

Теперь оба параметра ибудем считать неизвестными. Нас интересует доверительный интервал для. В этом смысле параметрявляется мешающим. Выберем

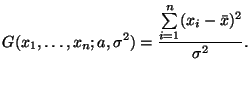
Заметим, что функция определена таким образом, что при заданной выборке ее значения зависят лишь от параметра. Что касается распределения случайной величины, то по теореме Фишера (см.8.3) оно является -распределением сстепенями свободы и, следовательно, не зависит от неизвестных параметров. Фиксируя, такие, что, и рассуждая как в (47), приходим к следующему -доверительному интервалу для:

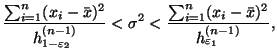
который, используя обозначение (30), можно переписать так

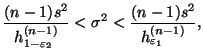
Доверительный интервал для среднего при неизвестной дисперсии

Как и в предыдущем пункте, оба параметра исчитаются неизвестными, при этомявляется мешающим параметром. По теореме Фишера

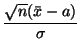и

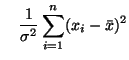
независимы и имеют распределения и-распределение сстепенью свободы соответственно. Следовательно, отношение

(48)

имеет распределение Стьюдента с степенью свободы. Выберем функциюравной правой части (48):

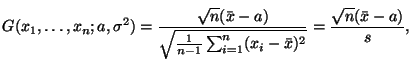
где -- выборочная дисперсия, определенная формулой (30). Функция не зависит явно от мешающего параметра. Обозначая черезквантиль распределения Стьюдента сстепенью свободы, получим, что неравенство

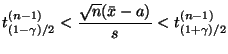
выполнено с вероятностью . Отсюда получаем-доверительный интервал для:

Так как распределение Стьюдента симметрично, то по Предложению 3.3

Поэтому доверительный интервал можно записать в виде

(49)

Таким образом, выборочное среднее является серединой этого интервала.

Пример 8.2  

Обратимся к Примеру 6.4.Предположим, что каждая из выборокивзята изнормальногораспределения снеизвестнымипараметрами --исоответственно. (О том, на основании чего можно сделать такое допущение, мы поговорим позже в9.5.)

Наша цель -- найти доверительные интервалы для и, теоретических значений содержания углерода и прочности на разрыв стали GS50. Напомним, что объем каждой из выборок. Зафиксируем доверительную вероятность, близкую к единице, скажем. По таблице распределения Стьюдента на стр.определим приближенно, что. Вспоминая значенияи, найденные в Примере6.5на стр., вычисляем

и, пользуясь формулой (49), получаем -доверительный интервал для процентногосодержания углерода

и -доверительный интервал для значенияпрочности на разрыв

Лабораторная работа №12. Основы теории оценивания

Статистик имеет дело с данными, подверженными случайной изменчивости. Их поведение характеризуется некоторым законом распределения вероятностей. Такой закон, как правило, содержит неизвестные величины, которые принято считать параметрами закона. В силу случайной изменчивости наблюдаемых данных, нельзя, основываясь на них, указать совершенно точное значение параметров. Приходится довольствоваться лишь приближенными значениями. Итак, математический статистик работает с такими величинами: - случайной величиной, которую он никогда не наблюдает, но которую считает "душой" изучаемых им данных, причиной, их породившей. Эта величина определяется некоторыми параметрами; - изучаемыми данными, которые получены, как реализация случайной величины. Например, случайной величиной является точное время. Её реализациями - показания часов, доступных для статистика. Задача статистика - по показаниям n часов t₁,...,t_n максимально точно установить время. Кроме того он обязан охарактеризовать точность установленного значения. Он выполняет оценивание искомой величины в виде t = t₀ + ξ(a,σ), где t₀ - истинное время в момент исследования, ξ(a,σ) - случайная величина, характеризующая отклонение от истинного значения, t₀, a, σ - параметры, величина ξ характеризуется законом распределения, вероятностями того, что она принимает различные значения. Оцениванием в статистике называют правило вычисления приближенного значения параметра на основе наблюдаемых данных. Оценка - это приближенное значение параметра, найденное по наблюдаемым данным. При построении оценок для практического применения, к оценкам предъявляются три основных требования:

• точность, то есть близость к истинному значению параметра, в примере ξ(a,σ) должно быть мало;

• несмещенность, то есть требование, чтобы математическое ожидание оценки было равно истинному значению параметра, в примере ξ(a,σ) должно быть в среднем равно нулю;

• состоятельность, то есть требование, чтобы при увеличении числа наблюдений оценка сходилась по вероятности к истинному значению параметра. В примере при большом числе часов n значение ξ(a,σ) должно стремиться к нулю с вероятностью, стремящейся к единице.

Наилучших во всех отношениях оценок не бывает. Например, среднее арифметическое, широко распространенная оценка среднего значения случайной величины, обладает свойством оптимальности для нормально распределенных данных. Однако оно приводит к ошибкам, если среди данных есть выбросы, то есть резко выделяющиеся значения. Такие выбросы в экономике порождены грубыми ошибками в измерениях или опечатками, при которых может исчезнуть точка между рублями и копейками и зарплата возрастёт в сотню раз. Рассмотрим случайный процесс, связанный с историей нанесения на карту Великой Британии уточнённых границ её владений, разбросанных по всем частям света. Известно, что любая точка на Земле характеризуется двумя координатами - широтой и долготой. Сегодня любой школьник слышал о спутниковых приборах, задающих любую точку на Земле с точностью до метра. Однако в те времена даже подобный прибор не помог бы морякам, так как он не обнаружил бы на небе ни одного "опорного" спутника. Широта определялась непосредственно по высоте светил над горизонтом с помощью прибора "секстан", аналогичного современному теодолиту (подзорная труба плюс измеритель угла). Долгота представляет собой угол поворота земного шара, при котором совмещаются местный меридиан и выбранный за условный нуль гринвичский. Земля делает оборот в 360° почти за сутки, то есть за час она поворачивается на 15°, за 4 минуты - на 1°. Для определения долготы надо точно знать местное и гринвичское время. Если штурман говорит капитану: "Местный полдень, Сэр", а капитан знает время в этот момент в Гринвиче, то разность времени, делённая на 4 минуты, и определяет долготу местности в градусах. Сегодня всё было бы просто - позвонить в Гринвич и узнать их время. Но тогда радио ещё не было придумано. Если бы на корабле были кварцевые часы, которые уходят на долю минуты за год, проблемы тоже бы не было, но существовавшие тогда лучшие хронометры не обеспечивали необходимой для измерения долготы точности. Они за несколько месяцев плавания уходили от точного времени на десятки минут. И когда в 1831 году в кругосветное плавание для составления карт отправлялся корабль "Бигль", капитан корабля Фиц Рой, человек просвещенный и ученый, взял с собой 24(!) морских хронометра. Каждый хронометр показывал своё "гринвичское время". В данном исследовании случайная величина - момент, когда штурман определял точное местное время по какому-нибудь небесному светилу. "Душа" измеряемой случайной величины - истинное время в Гринвиче в этот момент. Такую величину обозначим ξ. Значение этой величины никогда не известно. Наблюдаемые значения случайной величины, это показания (разные) хронометров. Каждый из них несколько ошибался, но в целом они следовали за общей "душой", накладывая на неё свою случайную погрешность. Оценка случайной величины - это то гринвичское время, которое предполагал по наблюдаемым данным капитан. Пусть случайные величины x_i, i = 1,...,n, являются реализациями одной случайной величины ξ, то есть имеют одинаковое распределение (одну "душу"), причём для любого i среднее значение показаний равно одному и тому же числу: Е(x_i) = Е(ξ). Смысл этого утверждения таков: все часы не могут дружно отставать или спешить из-за конструктивных неполадок. В среднем, равновероятно, что они спешат или отстают. Кроме того, пусть они независимы. Другими словами, у них нет чего-то общего в группах. Так, матрос, записывающий показания часов, мог их регистрировать в одной последовательности. Тогда последние показания регистрировались бы на минуту позже первых. Или несколько часов могли висеть в тёплом месте и от нагрева дружно спешить. Предположение, что такого явления нет, соответствует условию независимости показаний в разных испытаниях. Самая простая задача оценивания - это определение вероятности некоторого события, например, того, что реальная (не обязательно правильная) монета выпадет гербом вверх. Определить вероятность события почти никогда нельзя непосредственно. Универсального метода, который позволял бы для произвольного события указать его вероятность, не существует. Можно оценить вероятность события А, если допустимо проводить независимые повторные испытания в ходе которых это событие наступает с постоянной вероятностью. Пусть в каждом из п испытаний вероятность р = Р(А) события А остается неизменной и результат каждого испытания независим от остальных. Обозначим через m случайное число тех испытаний из общего числа n, в которых произошло событие А. Говорят, что m - число "успехов" в n испытаниях Бернулли. Согласно статистическому определению вероятности, при большом n относительная частота m/n события А приближенно равна вероятности события наступления события А, то есть m/n ~ р, где р = Р(А). Докажем, что это следует из аксиоматики Колмогорова. В математическом анализе используется строгое понятие предела последовательности: при достаточно большом номере члена последовательности, его значение может быть сделано сколь угодно близким к предельному значению. Такое определение не соответствует реальной жизни, где крайне редко происходят совершенно невероятные события. Например, из первичного хаотического бульона возникает бактерия, способная воспроизводить себя. Или рыба создаёт нечто, которое сначала миллионы лет ей не надо (но развивается), а затем становится крылом. Или затапливается целый город (или страна). В теории вероятностей понятие предела толкуется в смысле, отличном от того, который вкладывается в него в математическом анализе. Определение теории вероятностей ближе к жизни. Оно не запрещает того, что в какой-то момент в последовательности будет число, резко отличающееся от других. Последовательность случайных величин u_n сходится по вероятности к р, если для любого числа ε > 0 вероятность того, что модуль разности |u_n - р| при n → ∞ меньше, чем ε, стремится к единице:

В теории вероятностей никакое событие не является достоверным, но событие: |u_n - р| ≤ ε практически достоверно при достаточно больших n. Докажем неравенство Чебышева. Пусть ξ - случайная величина, имеющая математическое ожидание Е(ξ) = а и дисперсию D(ξ) = σ², ε - положительное число. Тогда вероятность события, состоящего в том, что центрированная (Е(ξ) - а) и нормированная случайная величина превышает ε менее, чем ε^-2:

Действительно, σ² = Е(ξ - а)². При вычислении среднего в правой части, выделим две области значений ξ. Для тех ξ, у которых |ξ - а| < εσ, сумма (или интеграл) соответствующих произведений неотрицателен. Для тех ξ, у которых |ξ - а| > εσ, сумма (или интеграл):

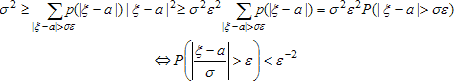
Любопытный частный случай: σ = 0. При этом ясно, что |ξ - а| = 0, то есть ξ = а. Докажем теорему Чебышева. Пусть х₁,...,х_n - независимые одинаково распределенные случайные величины, имеющие математическое ожидание и дисперсию. То есть каждый x_i суть реализация случайной величины ξ, причём Е(ξ) = Е(x_i) = а, D(ξ) = D(x_i) = σ². Тогда для любого ε > 0:

Доказательство. Дисперсия среднего арифметического:

Рассмотрим случайную величину η_n, представляющую собой среднее арифметическое n наблюдений. Её среднее и дисперсия . Наблюдаемыми реализациями η_n являются . В соответствии с неравенством Чебышева для случайной величины η_n, вероятность её отклонения от среднего значения на величину, большую чем стремится к нулю:

Вероятность противоположного события стремится при больших n к 1: P(|η_n - a|) → 1. Значит, последовательность случайных величин n сходится по вероятности к a. Вернемся к измерению времени на "Бигле". Показание каждого хронометра x_i, i = 1,...,n - это измерение, независимое от других приборов. Подразумевается, что конструкция хронометра такова, что его работе отсутствует систематическая ошибка. Это значит, что одни экземпляры хронометров могут "уходить вперёд", другие "отставать", но эти ошибки случайные, связанные с изготовлением данного образца. Математически это означает, что среднее время - истинное. Качество конструкции и технологии изготовления хронометров характеризуется тем, насколько однородна по точности хода вся продукция в целом. Математически это выражается разбросом показаний отдельных приборов, т.е. дисперсией случайных величин x_i. Дисперсия среднего в n = 24 раз меньше, чем дисперсия отдельного хронометра. Поэтому "среднее время", определённое по 24 хронометрам в среднем ближе к истинному времени почти в 5 раз, чем время любого отдельного хронометра.