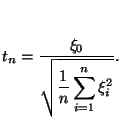8.2 Вероятностные распределения, связанные с нормальным

Подпункты этого параграфа:

Здесь мы кратко обсудим распределение хи-квадрат и распределение Стьюдента, играющие исключительную роль в статистике. Наше изложение близко содержанию 2.6 книги.

Хи-квадрат распределение

Пусть -- независимые стандартные нормальные случайные величины ().-распределением сстепенями свободы называется распределение следующей случайной величины:

(44)

Это распределение сосредоточенно на положительной полуоси и имеет плотность

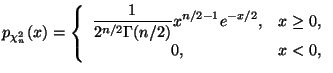
где 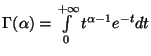-- гамма-функция.

Упражнение 8.2  

Начертить графики плотности прии.

Упражнение 8.3  

Найти и.

Квантили распределения будем обозначать,. По определению они являются решениями уравнения

(45)

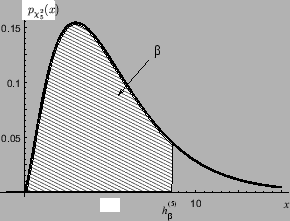
где -- функция хи-квадрат распределения сстепенями свободы. На этом чертеже изображены плотностьи ее квантиль.

Для значений функции распределения имеются таблицы, из которых находят квантили. Кроме этого, хи-квадрат распределение интегрировано в большое число прикладных компьютерных программ . На страниценастоящей брошюры также приведена небольшая таблица квантилей хи-квадрат распределения.

Распределение Стьюдента

Это распределение получило свое название от псевдонима Student, которым английский ученый Госсет подписывал свои работы по статистике.

Пусть -- независимые стандартные нормальные случайные величины. Распределением Стьюдента сстепенями свободы называется распределение следующей случайной величины:

(46)

Если вспомнить введенную формулой (44) случайную величину  , то можно сказать, что отношениеимеет распределение Стьюдента. Плотность этого распределения представляет собой симметричную функцию, задаваемую формулой

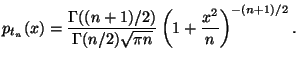
По форме график функции напоминает график плотности стандартного нормального закона, но с более медленным убыванием ``хвостов''. Припоследовательность функцийсходится к функции, которая есть плотность распределения. Чтобы понять, почему этот факт имеет место, следует обратить внимание на то, что по закону больших чисел знаменатель выражения (46) при стремится к.

На чертеже представлены плотность распределения Стьюдента и плотность стандартного нормального закона. В дальнейшем нам понадобятся квантили распределения, которые мы будем обозначать,,

Небольшую таблицу квантилей распределения Стьюдента можно найти на странице .

8.3 Теорема Фишера для нормальных выборок

В этом параграфе мы приводим теорему, впервые доказанную Р.А. Фишером в 1925 г. Она существенно облегчает статистический анализ независимых выборок из нормального распределения.

Теорема Фишера. Пусть -- независимая выборка из распределения. Тогда

1. выборочное среднее 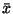и выборочная дисперсия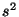независимы;

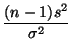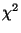2. имеет -распределение с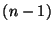степенью свободы.

С доказательством этой теоремы можно познакомиться, обратившись к книгам .

8.4 Доверительное оценивание параметров нормальных выборок

Подпункты этого параграфа:

Всюду в этом параграфе мы рассматриваем независимые выборки из нормального распределения. Мы построим доверительные интервалы для параметров распределения при различных предположениях относительно статистической модели.

Доверительный интервал для среднего при известной дисперсии

Предположим, что параметр неизвестен, а дисперсия-- известное фиксированное число. Пусть-- доверительная вероятность. Применим метод, изложенный в8.1. Выберем функцию

Из Упражнения 4.7 вытекает, что имеет нормальное распределение. Нетрудно видеть, что это стандартное нормальное распределение. Следовательно,. Выбираяи,, заключаем, что неравенство

выполнено с вероятностью . Решая его, находим доверительный интервал:

Если теперь заметить, что , то-доверительный интервал можно записать еще проще:

Замечательно то, что выборочное среднее является серединой этого интервала, а его длина стремится к нулю с увеличением объема выборки.