[Править] Параметрические и непараметрические гипотезы.

Статистические гипотезы бывают параметрические и непараметрические. Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой (напомним, что параметр может быть и многомерным). Предположение, при котором вид распределения неизвестен (то есть не предполагается, что оно входит в некоторое параметрическое семейство распределений), называется непараметрической гипотезой. Таким образом, если распределение F(x) результатов наблюдений в выборке согласно принятой вероятностной модели входит в некоторое параметрическое семейство, то естьF(x) =F(x;θ₀) при некотором θ₀Θ, то рассматриваемая гипотеза — параметрическая, в противном случае — непараметрическая.

Если и H₀иH₁— параметрические гипотезы, то задача проверки статистической гипотезы — параметрическая. Если хотя бы одна из гипотезH₀иH₁— непараметрическая, то задача проверки статистической гипотезы — непараметрическая. Другими словами, если вероятностная модель ситуации — параметрическая, то есть полностью описывается в терминах того или иного параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы — параметрическая. Если же вероятностная модель ситуации — непараметрическая, то есть ее нельзя полностью описать в терминах какого-либо параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы — непараметрическая. В примерах 11-13, 16, 17, 20-22 даны постановки параметрических задач проверки гипотез, а в примерах 14, 15, 18, 19, 23-25 — непараметрических. Непараметрические задачи делятся на два класса: в одном из них речь идет о проверке утверждений, касающихся функций распределения (примеры 14, 15, 18, 19, 25), во втором — о проверке утверждений, касающихся характеристик распределений (примеры 23, 24).

Статистическая гипотеза называется простой, если она однозначно задает распределение результатов наблюдений, вошедших в выборку. В противном случае статистическая гипотеза называется сложной. Гипотеза 2 из приведенного выше списка, нулевые гипотезы в примерах 11, 12, 14, 20, нулевая и альтернативная гипотезы в примере 21 — простые, все остальные упомянутые выше гипотезы — сложные.

Доверительные интервалы

Оценки параметров позволяют по выборке вычислить некоторые значения, которые ``приближают'' неизвестные параметры. Существует другой подход к тому, чтобы извлечь информацию о неизвестных параметрах. Он состоит в том, чтобы, основываясь на данных наблюдений, определить границы, в которых с заданной степенью достоверности лежит неизвестный параметр.

8.1 Понятие доверительного интервала

Будем считать, что независимая выборка взята из распределения, зависящего от скалярного параметра. Будем обозначать черезраспределение вероятностей, соответствующее значениюнеизвестного параметра.

Определение  

-доверительным интерваломназывается интервал видагдетакой, что

Число называютдоверительной вероятностью.

Другими словами, доверительный интервал обладает тем свойством, что, во-первых, его границы вычисляются исключительно по выборке (и, следовательно, не зависят от неизвестного параметра), и, во-вторых, он накрывает неизвестный параметр с вероятностью .

Значение доверительной вероятности выбирается заранее, этот выбор определяется конкретными практическими приложениями. Смысл величины-- вероятность допустимой ошибки. Часто берут значенияи т.п. Ниже мы приводим один изметодов построениядоверительных интервалов. Он состоит из трех этапов.

1. Выбираем функцию 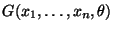, зависящую от выборки и от неизвестного параметра, такую, что ее функция распределения

не зависит от неизвестного параметра .

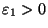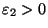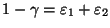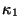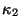2. Выбираем два числа итаким образом, чтобы. Подбираеми, удовлетворяющие условиям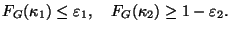

   (41)

4. Таким образом,

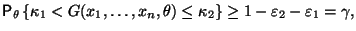
   (42)

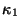6. причем и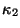не зависят от.

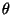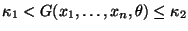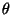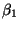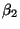7. Решим двойное неравенство относительно. В том случае, когда его решением является интервал, обозначим его левый и правый концы черезисоответственно. Естественно, они зависят от выборки: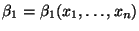,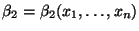. В силу (42)

Следовательно, -- искомый-доверительный интервал.

Замечание 8.1  

Описанная процедура, разумеется, не является универсальной. Во-первых, вопрос о выборе функции решается в каждом конкретном случае и по этому поводу нет общих рекомендаций. Во-вторых, совершенно не гарантировано, что решением неравенства в п. 3 будет интервал конечной длины. Вместе с тем, во многих важных случаях изложенный выше метод приводит к хорошим доверительным интервалам. Например, оправдано применение такого метода в случае, когда при каждойфиксированнойвыборкефункцияявляется строго монотонной и непрерывной по переменной.

Замечание 8.2  

В силу неоднозначности выбора функции и чисели, можно заключить, что-доверительный интервалнеединственен.

Пример 8.1  

Пусть -- независимая выборка из равномерного распределения в отрезкес неизвестным параметром:

Пусть задана доверительная вероятность . Построим доверительный интервал для.

1. Рассмотрим функцию 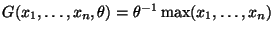. Вычислим ее функцию распределения:

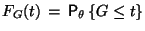
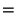
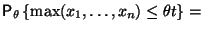
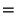
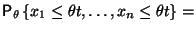
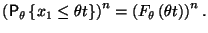
3. Таким образом,

4. 

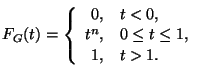
5. и, следовательно, не зависит от .

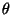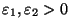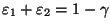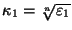6. Зафиксируем так, чтобы. Тогдаи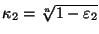удовлетворяют (41).

7. Решая неравенство 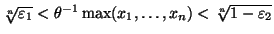, получаем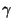-доверительный интервал для: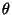

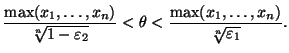
   (43)

Очевидно, что следует отдавать предпочтение тем -доверительным интервалам, у которых длина короче.

Упражнение 8.1

Показать, что при математическое ожидание длины доверительного интервала (43) стремится к нулю.