7.6. Модель сигнала в многоэлементной антенне

Современные пассивные и активные гидролокаторы имеют многоэлементные антенны и модель сигнала на входе антенны строится на основе модели излучённого сигнала и учёта влияния канала распространения, которые для бездисперсного случая сводится к внесению задержкив элементы сигнала и ослабления. В векторной форме записи сигнал на входе М-элементной антенны имеет вид:

(7.55)

где для широкополосного гауссовского источника элементы сигнала с когерентным волновым фронтом имеют видв соответствии с моделью канала, представленной на рис.1.4. В этой модели задержкаучитывается импульсной характеристикой, соответствующей дельта-функции .

Основными статистическими характеристиками такого сигнала являются взаимные корреляционные функциимежду элементами, а также взаимные спектральные плотности мощности, которые приимеют вид:

(7.56)

(7.57)

Для сигналов с когерентным волновым фронтом задержка , определяемая размещением элементов в пространстве, легко учитывается, поэтому полной характеристикой сигнала является матрица взаимных корреляционных функций или спектральных плотностей мощности при

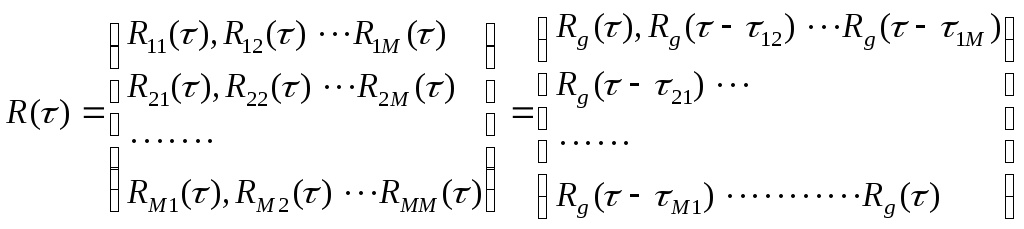(7.58)

является симметричной, положительно определённой матрицей.

(7.59)

является комплексной матрицей, а поскольку , то при любом фиксированном значении частотыявляется Эрмитовой матрицей, которую можно представить в виде произведения вектора-столбца

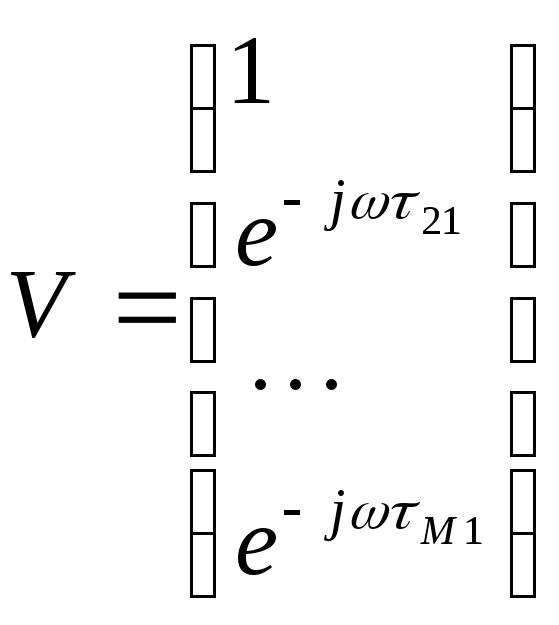(7.60)

на эрмитово сопряжённый (комплексно сопряжённый транспонированный вектор

(7.61)

при этом ранг матрицы равен 1.

Для моделей сигналов активных систем в качестве источника выбирают процессы со случайной амплитудой, случайной фазой, случайными амплитудой и фазойБолее сложными являются модели со случайными амплитудной, частотой и фазовой модуляцией.

7.7. Модели помех

В качестве помех работе ГАС могут выступать электрические шумы (преобразователей, электронных схем) и акустические шумы моря, носителя, локальных источников. Особым видом помех работе активных ГАС является морская реверберация, параметры которой существенно зависят от вида излучаемого сигнала. Принято считать, что современный уровень преобразовательной и электронной техники позволяет снизить уровень электрических помех до пренебрежимо малого по сравнению с акустическими, однако в ряде случаев это положение может быть несправедливым. Это относится, например, к стационарным низкочастотным системам, когда внешний фон весьма мал, а внутренние шумы аппаратуры резко возрастают с понижением рабочих частот. Приемлемой моделью во многих практических приложениях является помеховый процесс с нормальным распределением, имеющий во временной области -мерную плотность распределения вероятностей

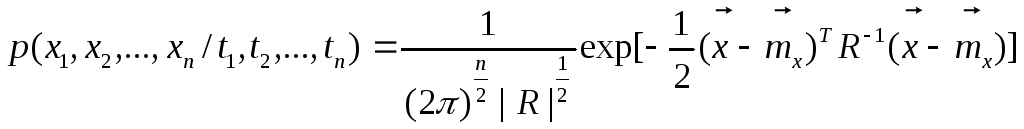(7.62)

.

Такой процесс может быть результатом суперпозиции многочисленных составляющих со взаимно независимыми амплитудами и фазами, что определяет временную корреляционную матрицу в виде:

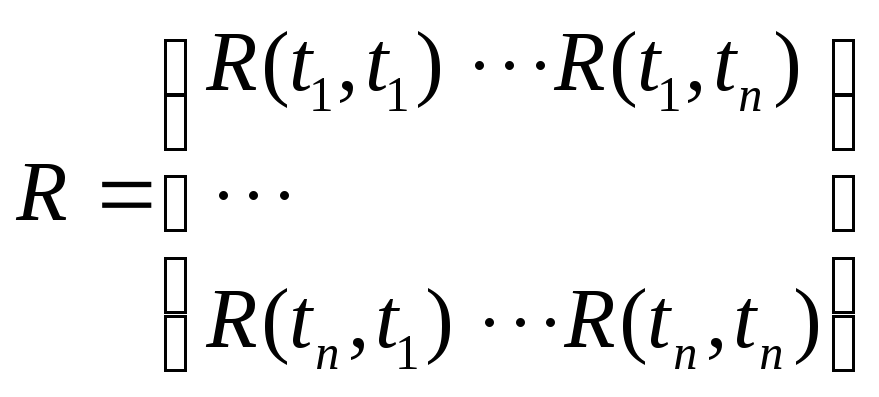(7.63)

Помеховый процесс, формируемый внутренними источниками в ГАС, по своим свойствам близок к «белому шуму, т.е. случайному процессу, имеющему постоянную в бесконечной полосе частот спектральную плотность мощности и близкую к дельта-функции ковариационную (корреляционную) функцию. Если складываются некоррелированные шумы, то мощность суммарного шума представляет собой сумму мощностей составляющих шумов . Аналогичные соотношения справедливы для ковариационных функций и для функций спектральной плотности мощности.

Большое значение для оценки помехоустойчивости приёмных трактов ГАС имеет знание статистических характеристик огибающей процесса в модели типа

, (7.64)

где - функция, медленно изменяющаяся во времени.

При гауссовском процессе по основному колебанию огибающая имеет релеевское распределение амплитуд

(7.65)

и равномерное распределение фаз в интервале 2, т.е.

Если помеховый процесс содержит наряду с ограниченным по спектру шумом гармоническую составляющую, то плотность распределения огибающей описывается функцией

(7.65)

соответствующий обобщённому закону Рэлея, или закону Райса. При малых значениях отношения амплитудыгармонической составляющей к эффективному напряжению шумаплотность распределения близка к релеевской, а при очень больших – к нормальной с математическим ожиданием, равным примерно.

Специфическим видом помехи является реверберационнй процесс, формируемый наложением в точке приёма множества независимых случайных возмущений, рассеянных неоднородностями окружающей среды. Реверберация не является стационарным процессом, но если допустить изотропность рассеивающих свойств среды и их стационарность, то нестационарный процесс реверберации можно описать в виде произведения двух функций – регулярной и стационарной случайной , гдеявляется некоторой монотонно изменяющейся функцией видас величинойдля объёмной,n=2 для поверхностной и n=3 для донной реверберации. Знание вида функции позволяет стационаризовать процесс, а статистические характеристики рассматривать для стационарной части Ф(t), что приводит для огибающей к релеевскому закону, т.е. аналогичному шумовому процессу с ограниченным спектром.