Лекция 7. Статистические модели процессов и полей

(8часов+6 часов ПЗ)

В.Б. Митько, кафедра Морских информационных технологий РГГМУ

Основные вопросы лекции:

1. Корреляционные и спектральные характеристики

2. Связь между корреляционными и спектральными характеристиками

3. Стационарное, однородное, изотропное поля

4. Модели сигналов

5. Функция неопределённости сигналов

6. Модель сигнала в многоэлементной антенне

7. Модели помех

8. Пространственно-временное представление

9. Пространственно-частотное представление

Введение

В гидроакустических информационных системах наиболее соответствующими реальным условиям являются вероятностные модели, приводящие к необходимости развития статистических методов описания сигналов и помех, систем в целом и условий их использования. Случайные процессы, с которыми приходится иметь дело в гидроакустике, могут быть непрерывными и дискретными. Чаще в гидроакустике процессы являются непрерывными, поскольку за время излучения и приёма сигнала резкие изменения условий в реальных ситуациях наблюдаются крайне редко. Случайные процессы (СП) могут быть скалярными и векторными, стационарными и нестационарными.

Математическая модель СП строится в предположении, что он может быть представлен ансамблем реализаций, а с помощью вероятностных характеристик свойства СП могут быть представлены столь же исчерпывающе, сколь и посредством ансамбля реализаций. Основными характеристиками СП являются функция и плотность распределения вероятностей, ковариационные и корреляционные функции, спектральные функции. Отнесение процесса к классу случайных обусловливается либо его физической природой, либо степенью познания. Процессы, для которых невозможно проследить характер причинно-следственных связей, называют несингулярными. Для таких процессов невозможно прогнозировать мгновенные значения, что характерно, например, для процессов морской реверберации, теплового шума преобразователей и т.п. Процессы, природа которых позволяет описать их с любой степенью достоверности, называют сингулярными. Это характерно для детерминированных процессов со случайными параметрами, например . При наличии определённых априорных данных возможно прогнозирование сингулярных процессов и в зависимости от этого они могут быть случайными или детерминированными. Несингулярные процессы могут быть только случайными.

В зависимости от возможностей прогнозирования значений СП они могут подразделяться на марковские и немарковские. Для немарковских процессов прогнозирование определяется полнотой учёта информации о значениях процесса в моменты, предшествующие данному, а для марковских СП качество прогнозирования не зависит от значений процесса в моменты времени, предшествующие данному. Марковские и немарковские несингулярные процессы характеризуются тем, что предел качества прогнозирования определяется природой процесса и в принципе не может достичь уровня достоверности. В гидроакустике наиболее распространёнными являются модели, основанные на предположении «марковости» процессов, когда их можно описывать вероятностью перехода значений процесса из состоянияв момент времени

в состояние в момент времени. Через неё можно выражать плотности вероятностей произвольного порядка и в соответствии с определением марковского процесса

, (7.1)

где- одномерная плотность вероятности.

Наряду с марковскими процессами в гидроакустике оперируют с марковскими цепями, т.е. с дискретными марковскими процессами.

В практических приложениях используются теоретические (неслучайные) и выборочные (случайные) характеристики, с которыми соответственно оперирует теория вероятностей и математическая статистика. Важное значение имеют начальные и центральные моменты функции, в частности, начальная моментная функция первого порядка (среднее значение) и центральная моментная функция второго порядка (дисперсия). Теоретические и выборочные значения этих величин равны:

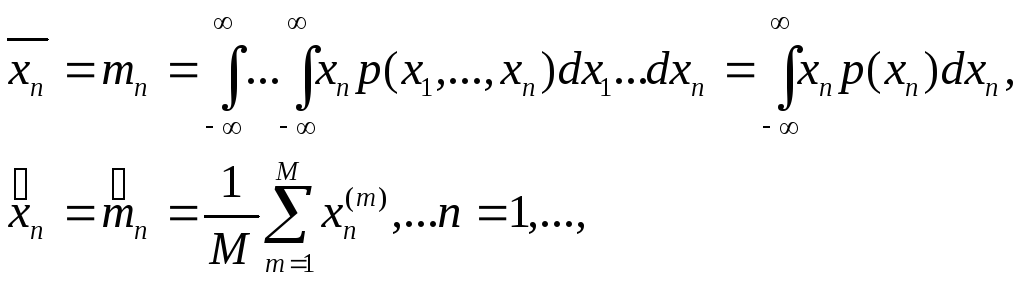(7.2)

(7.3)

для средних значений;

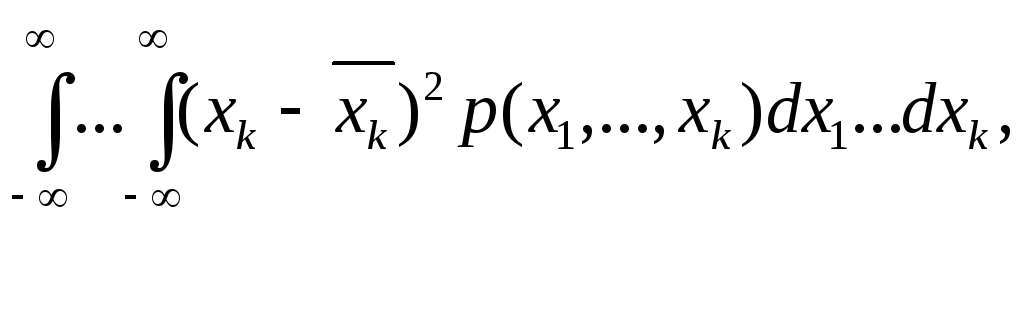(7.4)

(7.5)

для дисперсии.

В гидроакустике СП могут быть нестационарными и стационарными. Хотя большинство процессов являются нестационарными, можно выбирать такие интервалы, на которых СП близок к стационарному в узком или широком смысле. Стационарный в узком смысле СП – это процесс, у которого все конечномерные функции распределения вероятностей инвариантны относительно сдвига во времени. Стационарный в широком смысле СП – это процесс с конечной дисперсией, у которого математическое ожидание и ковариационная функция инвариантны относительно сдвига во времени. В большинстве практических приложений стационарные процессы полагают эргодическими, что позволяет заменить обработку по ансамблю реализаций обработкой во времени.