
ТОЭ3 / Практикум _3 Нелин пост
.pdf
НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Занятие1
Цели занятия:
1.Научиться находить рабочую точку графическим методом в неразветвленной цепи с одним нелинейным элементом.
2.Научиться находить рабочую точку графическим методом в разветвленной цепи с одним нелинейным элементом.
3.Научиться находить рабочую точку графическим методом в разветвленной цепи с несколькими нелинейными элементами.
Для цепи с двумя последовательно соединенными элементами, один из которых – линейный (рис. 6.1), рационально отыскание рабочей точки на пересечении вольт-амперной характеристики (ВАХ) нелинейного элемента (НЭ) с зеркальным отображением ВАХ линейного элемента.
I |
НЭ1 |
R |
|
U |
U 1 |
U 2 |
|
|
Рис.6.1 |
|
|
Решение этим методом поясняет рис. |
6.2. Строим ВАХ НЭ I(U1). В |
||
рабочей точке на основании |
второго |
закона Кирхгофа |
напряжение |
U1 =U −U2 . Построим график |
I(U −U2 ), |
который является |
зеркальным |
отображением графика I(U2 ) , смещенного вправо на величину входного
напряжения U . Так как ВАХ линейного элемента является прямой линией, то для построения графика I(U −UЛЭ) нужны только две точки, одна из
которых с координатами (U,0). Очевидно, что графики пересекаются в рабочей точке А. Находим соответствующие ей значения тока I и напряжений U1 и U2 .
Для разветвленной схемы с одним нелинейным элементом, ток в котором и надо найти, в решении как промежуточный можно использовать метод эквивалентного генератора. Делим схему на две части: НЭ и всю остальную часть схемы, которая является активным двухполюсником.
Активный двухполюсник заменим эквивалентным ему генератором. Активный двухполюсник является линейной цепью, расчет которой намного проще, чем нелинейной. ЭДС генератора Ег равна напряжению холостого
хода на зажимах активного двухполюсника. Сопротивление Rг – это

эквивалентное сопротивление пассивного двухполюсника относительно входных зажимов. Пассивный двухполюсник получаем из активного, закорачивая источники ЭДС и разрывая источники тока. Полученная схема представляет собой последовательное соединение нелинейного и линейного элементов.
I |
I(U–U2) |
I(U1 ) |
|
I(U-U2 ) |
|
I |
A |
|
|
|
U1 |
U |
U2 |
Рис. 6.2
Рабочую точку рационально найти на пересечении ВАХ НЭ и зеркального изображения ВАХ линейного элемента (рис. 6.2). График I(Ег −URг ) является прямой линией, зеркально отображающей график
I (URг ), смещенный вправо на величину Ег. Для его построения нужны две
точки. Одна из них с координатами (Ег,0).
Для построения второй точки можно задаться произвольным значением тока I j . Соответствующее ему напряжение U R j = RгI j отложим от
значения Ег влево. Отыскав рабочую точку А, найдем соответствующее ей значение тока I.
Задача1
Вычислить сопротивление R линейного элемента в схеме рис. 6.3, если входное напряжение U =120 В, напряжение на лампочке Uл = 75 В, ВАХ
лампочки задана табл. 6.1.
I R
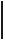 U
U
Рис.6.3
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
||
|
1. Построим ВАХ лампочки (рис. 6.4). |
|
|
|
|
|
|
|||||||||
|
|
I, А |
|
|
|
|
|
|
ВАХ лампочки |
|
|
|
|
|
||
|
|
0,7 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
A |
|
|
К задаче 5 |
|
|
|
|
|
||
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
К задаче 2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
40 |
|
80 |
120 |
160 |
|
200 U, В |
|
||||
|
|
|
|
|
|
|
|
Рис.6.4 |
|
|
|
|
|
|
|
|
|
2. Сопротивление R = U R . |
|
|
|
|
|
|
|
|
|||||||
|
3. По |
|
второму |
I |
закону |
|
Кирхгофа |
|
напряжение |
|||||||
|
|
|
|
|
||||||||||||
U R =U −Uл =120 −75 = 45 В. |
|
|
|
|
|
|
Uл = 75 В |
ток |
||||||||
|
4. Найдем |
ток |
|
схемы |
по |
ВАХ |
лампочки. При |
|||||||||
I ≈ 0,425 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тогда R = |
45 |
|
=106 Ом. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
0,425 |
|
|
|
|
|
|
|
|
|
Таблица 6.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U, |
0 |
1 |
20 |
40 |
|
60 |
80 |
10 |
120 |
14 |
160 |
18 |
200 |
220 |
240 |
260 |
B |
|
0 |
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
I, |
0 |
0, |
0, |
0, |
|
0,3 |
0,4 |
0,5 |
0,5 |
0,6 |
0,6 |
0, |
0,7 |
0,7 |
0,7 |
0,75 |
A |
|
1 |
18 |
3 |
|
8 |
5 |
|
5 |
|
5 |
7 |
2 |
3 |
4 |
|
Задача2
Найти ток в схеме рис. 6.3, если U = 200 В, R = 400 Ом.
Решение

Отыщем рабочую точку на пересечении ВАХ лампочки и зеркального отображения ВАХ линейного элемента, которое можно построить по двум точкам. Первая из них с координатами (200 В; 0). Для построения второй точки зададимся произвольным значением тока, например I j = 0,5 А. Тогда
UR j = R I j = 400 0,5 = 200 В. Отложим напряжение UR j от U = 200 В
влево. Получим вторую точку с координатами (0; 0,5 А). Рабочая точка А находится на пересечении двух графиков (см. рис. 6.4). Ей соответствует значение тока I ≈ 0,38 А.
Задачи 3 и 4 решите самостоятельно.
Задача3
Вычислить входное напряжение в схеме рис. 6.5, если ток I = 0,18 А.
I
 U
U
Рис.6.5
Ответ: U = 40 В.
Задача4
Вычислить мощность, потребляемую лампочкой в схеме рис. 6.3 при входном напряжении U =180 В, если при входном напряжении U = 220 В напряжение на лампочке Uл =127 В.
Ответ: Рл = 50 Вт.
Задача5
Вычислить мощность, потребляемую лампочкой в схеме рис. 6.6, если U =150 В, R1 =100 Ом, R2 = 400 Ом, ВАХ лампочки приведена на рис. 6.4.
|
R1 |
|
a |
U |
R2 |
|
b |
|
Рис.6.6 |
Решение

1. Заменим схему эквивалентной ей одноконтурной с помощью метода эквивалентного генератора. Разделим схему на две части: лампочку и всю остальную схему – активный двухполюсник (рис. 6.7), который заменим эквивалентным ему генератором. ЭДС генератора
Eг =Uхх = R2 Iхх .
Ток Iхх = R1 U+ R2 = 0,3 А.
Тогда Ег = 400 0,3 =120 В.
|
|
Iхх |
R1 |
|
|
|
|
|
|
a |
R2 |
|
|
U |
|
Uхх |
|
|
|
|
|
b |
|
|
|
|
Рис.6.7 |
|
|
Схема пассивного двухполюсника приведена на рис. 6.8. |
|||||
Сопротивление |
|
|
|
|
|
R = R = R1 R2 |
= 100 400 = 80 Ом. |
||||
г |
ab |
R1 |
+ R2 |
100 + 400 |
|
|
|
|
|||
R1 |
|
|
|
|
I Л |
а |
|
R2 |
|
Ег |
|
|
|
|
|
|
|
|
b |
Rг |
|
|
|
Рис.6.8 |
|
Рис.6.9 |
|
|
Получившаяся одноконтурная схема изображена на рис. 6.9.
2. Найдем рабочую точку на пересечении ВАХ лампочки с зеркальным отображением ВАХ линейного резистора. Одна точка для построения графика I (Eг −U Rг ) – с координатами (120 В; 0). Для построения второй

точки зададимся значением тока I j = 0,5 А. Тогда URj = Rг I j = 0,5 80 = 40
В. Отложим 40 В от 120 В влево и получим точку с координатами (80 В; 0,5 А). Проведем прямую через эти две точки (см. рис. 6.4). Рабочая точка В позволяет определить Uл ≈83 В и Iл ≈ 0,45 А.
Мощность, потребляемая лампочкой,
Pл =Uл Iл =83 0,45 ≈ 37,4 Вт.
Задачу 6 решите самостоятельно.
Задача6
Найти все токи в схеме рис. 6.6, если U = 380 В, R1 =300 Ом, R2 = 600
Ом.
Ответ: I1 = 0,8 А; I2 = 0,22 А; Iл = 0,58 А.
Задача7
Вычислить напряжение на входе схемы рис. 6.6, если R1 =50 Ом, R2 =100Ом, ток Iл = 0,2 А, ВАХ лампочки приведена на рис. 6.10.
II,, AА 
0,30,3
0,20,2
0,10,1
50 100100 150150 200200 U,U, ВВ
РисРис.6..106.10
Решение
1. По ВАХ лампочки найдем напряжение между двумя узлами, равное напряжению на лампочке:
U12 =Uл =100 В.
2. Вычислим ток I2 по закону Ома

I2 = U12 =100 =1 А.
R2 100
3. Вычислим ток I1 по первому закону Кирхгофа
I1 = I2 + Iл =1+ 0,2 =1,2 А.
4. Вычислим входное напряжение по второму закону Кирхгофа
U = R1 I1 +U12 =50 1,2 +100 =160 В.
Задача8
Найти ток в неразветвленной части цепи схемы рис. 6.11, если U =100 В, все лампочки одинаковые. ВАХ лампочки приведена на рис. 6.12.
I
I1 |
I2 |
|
U
Рис. 6.11
Решение
1.По ВАХлампочки найдемток I2 = 0,6 А.
2.В ветви с последовательным соединением двух одинаковых
лампочек на каждой лампочке напряжение Uл = U2 = 50 В.
3.По ВАХ лампочки найдем ток I1 = 0,4 А.
4.По первому закону Кирхгофа найдем ток
I = I1 + I2 = 0,4 + 0,6 =1 А.
Задачи 9–11 решите самостоятельно.

I, А |
|
|
|
0,8 |
|
|
|
0,6 |
|
|
|
0,4 |
|
|
|
0,2 |
|
|
|
50 |
100 |
150 |
U, B |
|
Рис. 6.12 |
|
|
|
Задача9 |
|
|
Найти напряжение на входе схемы рис. 6.11, если ток I1 = 0,4 А и все
лампочки одинаковые. ВАХ лампочки приведена на рис. 6.12. Ответ: U =100 В.
Задача10
Вычислить ток в неразветвленной части схемы рис. 6.11, если ток I1 = 0,4 А и все лампочки одинаковые. ВАХ лампочки приведена на рис. 6.12.
Ответ: I =1 А.
Задача11
Найти напряжение на входе схемы рис. 6.13, если ток I1 = 0,2 А и все лампочки одинаковые. ВАХ лампочки приведена на рис. 6.14.
I1 |
I2 |
U
Рис. 6.13
I, А
0,6
0,4
0,2
50 100 150 200 U,В
Рис. 6.14
Ответ: U = 200 В.
Занятие2
Цель занятия:
1. Научиться вычислять ток в нелинейном элементе методом итерации (последовательных приближений).
Сущность метода итерации (последовательных приближений) заключается в аналитическом решении системы алгебраических нелинейных уравнений. Статическое сопротивление нелинейного элемента должно быть задано в функции от тока или напряжения.
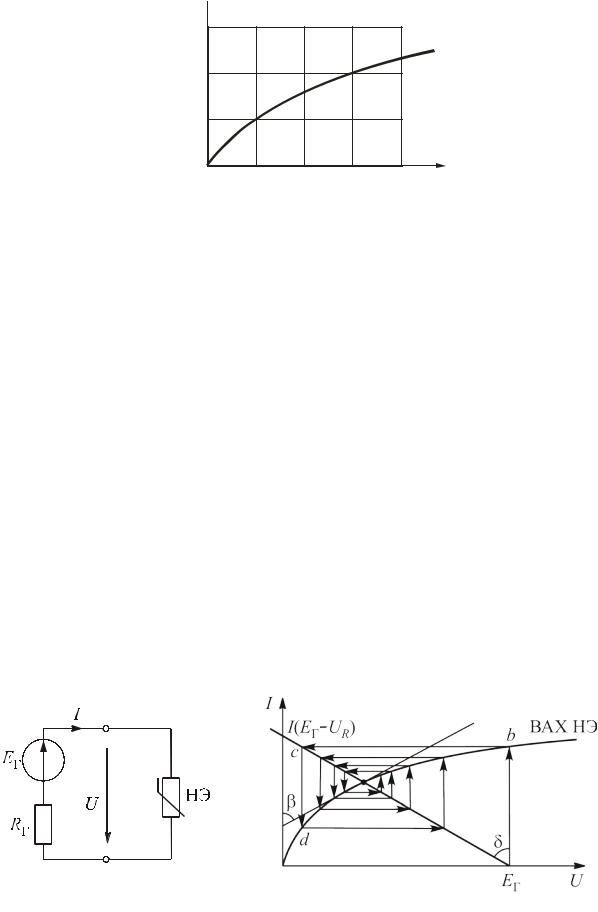
Пусть в схеме один нелинейный элемент (НЭ), ток в котором и надо найти. Остальную часть схемы (активный двухполюсник) заменим эквивалентным ему генератором (рис. 6.15).
Графическая иллюстрация решения методом итерации приведена на рис. 6.16.
Напряжение на нелинейном элементе U = Eг − RгI . Ток зависит от
статического сопротивления НЭ, которое, в свою очередь, зависит от напряжения, поэтому это уравнение является нелинейным: U = F(U ) .
Рис.6.15 |
Рис.6.16 |

Пусть напряжение в нулевом приближении U0 = Eг. На ВАХ НЭ
находим соответствующую рабочую точку b. Так как ток в схеме один, то току I0 на графике I(Eг − RгI) соответствует точка с. Напряжение на НЭ
U = Eг − RгI , поэтому переходим из точки с в точку d. Повторяя этот
процесс, получаем рабочую точку А.
Итерационный процесс может быть организован различными методами. Наиболее эффективным считается метод Ньютона – Рафсона.
Пусть нелинейное уравнение |
f (x) = 0 имеет единственный корень x = xk +1. |
||||
В окрестности этого корня функция f (xk +1) разлагается в ряд Тейлора: |
|||||
f (xk+1) = f (xk |
+∆xk ) ≈f (x k ) +∆xk |
f ′(xk ) =0 |
|
||
Отсюда следует xk +1 = xk + ∆xk , где ∆xk |
= h = − |
f (xk) |
– поправка |
||
f ′(xk ) |
|||||
|
|
|
|
||
к предыдущему решению. Из приведенных соотношений следует алгоритм метода Ньютона – Рафсона:
1. Задаем начальное приближенное значение искомого решения x0
(k = 0).
2. Определяем поправку h0 . Для ее вычисления по выражению функции находим производную.
3.Определяем уточненное значение корня x1 = x0 + h0 .
4.Повторяем процесс на следующем шаге и уточняем предыдущее решение до необходимой точности.
Геометрическая интерпретация метода приведена на рис. 6.17. В
качестве начального приближения примем U0 = Eг . В точке a проводим касательную к ВАХ НЭ, по касательной переходим на график I(Eг − RгI) в
точку b, далее в точку c на ВАХ НЭ, снова проводим касательную и т. д. Из рисунка видно, что число шагов, необходимых для нахождения решения в случае применения метода Ньютона – Рафсона, значительно меньше, чем при обычном итерационном процессе (рис. 6.16).
I |
|
a |
ВАХ НЭ |
|
|
|
|
|
b |
|
|
|
d |
|
|
c |
A |
I (Eг −U ) |
|
|
|
Eг U
Рис.6.17
