
Математика / 4015
.pdf
c x1 y2 e3 x1z2 e2 y1x2 e3 y1z2 e1 z1x2 e2 z1 y2 e1( y1z2 z1 y2 )e1 (z1x2 x1z2 )e2 (x1 y2 y1x2 )e3.
Последнее равенство можно записать в виде:
|
|
|
|
|
y z |
|
|
|
|
z |
|
x |
|
|
|
x |
y |
|
|
|
(3.7) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
c ab 1 |
1 |
e1 |
1 |
1 |
e2 |
1 |
1 |
e3 . |
||||||||||||||
|
|
|
|
|
y2 |
z |
2 |
z |
2 |
x2 |
x2 |
y2 |
|
|||||||||
Формулу (3.7) можно представить через определитель третьего порядка:
i j k
a |
|
x1 |
y1 |
z1 |
(3.8) |
b |
|||||
|
|
x2 |
y2 |
z2 |
|
Замечание. |
Если составить матрицу |
x |
y |
z |
|
из координат |
||||
x1 |
y1 |
z1 |
|
|||||||
|
|
|
|
2 |
2 |
2 |
|
|
|
|
векторов a и |
|
, |
то координаты векторного произведения a |
|
равны |
|||||
b |
b |
|||||||||
минорам второго порядка этой матрицы, полученным путем поочередного вычеркивания 1, 2 и 3-го столбцов, причем второй минор нужно взять со знаком «–».
Тогда модуль векторного произведения выражается формулой
|
|
|
|
y |
z |
|
2 |
|
x |
z |
|
2 |
|
x |
y |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a b |
|
|
|
|
. |
(3.9) |
||||||||||||
1 |
1 |
|
|
1 |
1 |
|
|
1 |
1 |
|
||||||||
|
|
|
|
y2 |
z2 |
|
|
|
x2 |
z2 |
|
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Необходимое и достаточное условие коллинеарности двух векторов
Два вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Пример 3.3
|
|
Найти векторное произведение a |
|
векторов a (3, 4, 8) |
b |
||||
и |
|
( 5,2, 1) . |
|
|
b |
|
|||
Решение. Составим матрицу из координат векторов:
3 4 8 .5 2 1
51

Обозначив координаты векторного произведения через x, y, z, имеем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
4 8 |
|
4 16 20, |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
3 8 |
|
|
( 3 40) 43, z |
|
3 |
4 |
|
6 20 14. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
5 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
|
|
|
|
|
|
|||||||||||
Итак, a |
|
|
|
(20,43, 14). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Пример 3.4 |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Найти |
|
|
|
|
площадь |
|
треугольника, |
заданного |
вершинами |
|||||||||||||||||||||||||||||||||||||
A(2, 3,1) , B(0,5, 4) , C(1,8,6) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Решение. Искомая площадь равна половине площади параллело- |
||||||||||||||||||||||||||||||||||||||||||||||
грамма, построенного на векторах |
|
|
|
|
|
и AC, (которая, |
как уже из- |
|||||||||||||||||||||||||||||||||||||||
AB |
||||||||||||||||||||||||||||||||||||||||||||||
вестно, равна |
|
|
|
|
|
|
|
|
|
|
|
). Находим |
|
|
( 2,8, 5), |
|
( 1,11,5) . |
|||||||||||||||||||||||||||||
|
|
AB |
AC |
|
AB |
AC |
||||||||||||||||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
5 |
|
|
2 |
|
|
5 |
|
|
|
2 |
8 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
(95,15, |
14). |
|||||||||
|
AB AC |
|
11 |
|
|
|
5 |
1 |
5 |
|
|
|
1 |
11 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
S 1 |
|
|
|
|
|
|
1 |
|
952 152 ( 14)2 |
1 |
|
|
9446 48,6. |
||||||||||||||||||||||||||||||||
|
|
AB |
AC |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 3.5
Коллинеарны ли векторы a (2, 5,1) и b ( 6,15, 3) ? Решение. Вычислим векторное произведение a b :
|
|
|
|
5 |
1 |
|
2 |
1 |
|
2 |
5 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
, |
|
|
, |
|
|
|
|
(0,0,0). |
a b |
|
15 |
3 |
6 |
3 |
6 |
15 |
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
Итак, векторы коллинеарны. Однако проще проверить пропорциональность соответствующих координат.
§ 3.4. Смешанное произведение трех векторов
Смешанным произведением трех векторов a, b , c называется скалярное произведение вектора a на векторное произведение b c .
52
Обозначается смешанное произведение трех векторов a, b , c следующим образом: a (b c) или (a,b,c) .
Геометрический смысл смешанного произведения
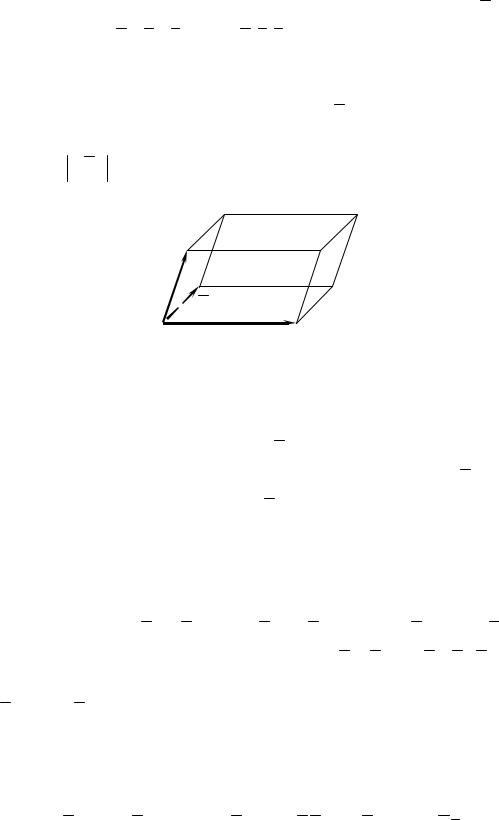
Модуль смешанного произведения a b c трех некомпланарных векторов равен объему параллелепипеда, построенного на этих векто-
рах, т. е. V a b c (рис. 3.5).
a
b
c
Рис. 3.5
Отсюда следует необходимое и достаточное условие компла-
нарности трех векторов: векторы a, b , c компланарны тогда и только тогда, когда их смешанное произведение равно нулю: a b c 0. Как видно из рис. 3.5, если векторы a, b , c компланарны (лежат в одной
плоскости), то объем соответствующего параллелепипеда равен нулю. Свойства смешанного произведения:
1. Круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей меняет знак на противоположный: a b c b c a ca b (b a c) (ac b ) (cab ).
2.Свойство распределительности: (a b )cd acd b cd .
3.Свойство сочетательности относительно числового множителя: (ma)b c m(ab c).
4.Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю: a a c 0 (векторы компланарны).
Пример 3.6
ab (3a 2b 5c) 3ab a 2ab b 5ab c 5ab c .
53

Вычисление смешанного произведения
Смешанное произведение трех векторов
a (x1, y1, z1), b (x2 , y2 , z2 ),
определяется формулой
x1 y1 z1 a b c x2 y2 z2 x3 y3 z3
c (x3 , y3 , z3 ) (3.10)
, |
(3.11) |
а следовательно, объем параллелепипеда, построенного на этих векторах, вычисляется по формуле
|
x1 |
y1 |
z1 |
|
|
|
|
|
|
||||
V mod |
x2 |
y2 |
z2 |
|
. |
(3.12) |
|
x3 |
y3 |
z3 |
|
|
|
Пусть требуется определить объем треугольной пирамиды с
вершинами в точках M1 (x1, y1, z1 ), M 2 (x2 , y2 , z2 ), M3 (x3 , y3 , z3 ), M 4 (x4 , y4 , z4 ) . Объем треугольной пирамиды M1M 2M3M 4 равен шес-
той части объема |
параллелепипеда, построенного на векторах |
|||
M1M2 , M1M3, M1M4 . |
Так |
как |
|
(x2 x1, y2 y1, z2 z1) , |
M1M 2 |
||||
M1M3 (x3 x1, y3 y1, z3 z1) , M1M 4 (x4 x1, y4 y1, z4 z1) , то
|
1 mod |
|
x2 x1 |
|
|
|
|||
V |
|
x |
x |
|
|
6 |
|
3 |
1 |
|
|
x4 |
x1 |
|
|
|
|
||
y2 y1 y3 y1 y4 y1
z2 z1
z3 z1 . (3.13) z4 z1
Необходимое и достаточное условие компланарности трех векторов (3.10) выражается равенством
x1 |
y1 |
z1 |
|
|
|
|
|||
x2 |
y2 |
z2 |
0 . |
(3.14) |
x3 |
y3 |
z3 |
|
|
Пример 3.7
Вычислить объем треугольной пирамиды, вершины которой на-
ходятся в точках M1(6,1,4), M 2 (1, 3,7), M3 (7,1,3), M 4 (2, 2, 5).
54

Решение. В соответствии с формулой (3.13) находим
V 1 mod |
|
1 6 |
|
3 1 |
7 4 |
|
1 mod |
|
5 |
4 |
3 |
|
||||
|
|
|
|
|
||||||||||||
|
7 6 |
|
1 1 |
3 4 |
|
|
1 |
0 |
1 |
|
||||||
6 |
|
2 6 |
|
2 1 |
5 4 |
|
6 |
|
|
|
4 |
3 |
9 |
|
||
|
|
1 mod |
|
5 |
4 |
|
2 |
|
23. |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
0 |
0 |
|
|
|
|
|||||||
|
|
|
6 |
|
|
4 |
3 |
|
13 |
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
D
L
A O C
O C
B
Рис. 3.6
Пример 3.8
Даны точки A( 2, 3,1), B(1, 1,2), C(2,4,2), D(1,2,6). Вычислить:
1)угол между ребром AD пирамиды ABCD и плоскостью ABC;
2)длину высоты DO пирамиды (рис. 3.6).
|
|
|
Решение. |
|
|
|
|
|
|
D на плоскость ABC (рис. 3.6). |
|||||||||||||||||||||||||
|
|
|
1. Пусть O – проекция точки |
||||||||||||||||||||||||||||||||
Тогда угол между векторами AD и |
|
|
|
|
– |
искомый |
|
угол. |
Пусть |
||||||||||||||||||||||||||
|
AO |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
, тогда |
|
|
ABC |
и |
|
DAO 90o LAD . |
Тогда |
||||||||||||||||||||
|
AL |
AB |
AC |
AL |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
3 1 |
|
3 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
AD (3,5,5), AB (3,4,1), |
|
AC (4,7,1) , |
|
|
|
, |
, |
|
||||||||||||||||||||||||||
|
|
AL |
|
7 |
1 |
4 1 |
4 7 |
|
( 3,1,5). |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
cos( LAD) |
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
AL |
AD |
|
|
0,46; LAD 62,5o. |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
59 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
AL |
AD |
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Значит, DAO 90o 62,5o 27,5o.
55
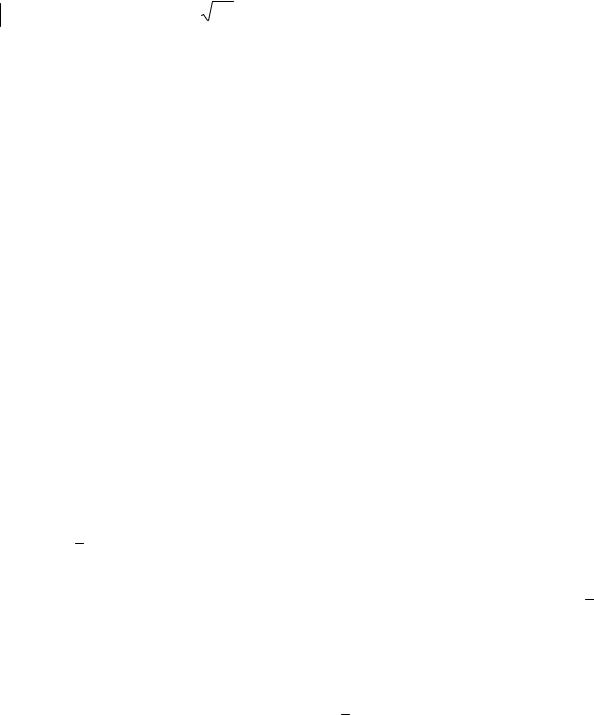
|
|
2. Как видно |
из рисунка, |
|
DO |
|
|
|
|
|
. Значит, |
||||||
|
|
AD |
AL |
||||||||||||||
DO |
|
|
|
|
|
|
|
cos( LAD) |
59 0,46 3,53. |
|
|
|
|
|
|
|
|
|
|
AD |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 3.5. Различные виды уравнения плоскости
Поверхностью называется совокупность точек пространства, координаты которых удовлетворяют уравнению следующего вида:
Ф(x, y, z). (3.15)
Может случится, что уравнению (3.15) удовлетворяют координаты лишь конечного числа точек. Например, рассмотрим уравнение
(x a)2 ( y b)2 (z c)2 0. Этому уравнению удовлетворяют координаты лишь единственной точки M(a, b, c). Рассмотрим еще такой пример: x2 y2 z2 1 0. В этом случае не существует ни одной точки, координаты которой удовлетворяли бы этому уравнению.
Вэтом случае поверхность называется мнимой поверхностью.
Втом случае когда переменные в уравнение (3.15) входят в первой степени, получается плоскость.
Параметрическое уравнение плоскости
Вектор a называется параллельным плоскости , если он лежит на прямой l, параллельной плоскости , или лежит на самой плоско-
сти . Плоскость вполне определяется, если задана точка M0 (x0 , y0 , z0 ) , лежащая в этой плоскости, и два неколлинеарных век-
тора a , b , каждый из которых параллелен плоскости . Пусть a = {a1, a2 , a3}, b = {b1,b2 ,b3}. Составим уравнение плоскости , прохо-
дящей через точку M 0 (x0 , y0 , z0 ) и параллельной векторам a , b . Возьмем в плоскости произвольную точку M (x, y, z) . Ясно, что
векторы |
a , |
|
|
, |
|
{x x0 , y y0 , z z0} компланарны. Так как |
||
|
b |
M0M |
||||||
векторы |
a , |
|
неколлинеарны, то вектор |
|
можно разложить по |
|||
b |
M0M |
|||||||
двум неколлинеарным напрвлениям a , b , т. е. имеет место уравнение
|
|
|
|
|
|
|
|
|
M0M |
ua vb. |
(3.16) |
||
Запишем равенство (3.16) в координатной форме: |
||||||
x x0 ua1 vb1, |
y y0 ua2 vb2 , |
z z0 ua3 vb3. |
||||
56

Отсюда получим:
x x0 ua1 vb1, |
|
|||
|
|
ua2 vb2 , |
(3.17) |
|
y y0 |
||||
z z |
0 |
ua |
vb . |
|
|
3 |
3 |
|
|
Уравнение (3.17) есть параметрическое уравнение плоскости.
Общее уравнение плоскости
Условие компланарности векторов a , b , M0M , а следовательно, уравнение плоскости можно записать в виде:
|
x x0 |
y y0 |
z z0 |
|
|
|
|
|
|||
|
a1 |
a2 |
a3 |
0 |
(3.18) |
|
b1 |
b2 |
b3 |
|
|
или в виде: |
|
|
|
|
|
|
Ax By Cz D 0 . |
(3.19) |
|||
Коэффициенты A, B,C |
одновременно в нуль не обращаются. |
||||
Уравнение (3.19) определяет плоскость в пространстве. Оно называется общим уравнением плоскости. Отметим частные случаи этого уравнения:
1. Если D 0 , то уравнение (3.19) принимает вид: Ax By Cz 0 . Значит, плоскость проходит через начало координат.
2. Если C 0, то уравнение (3.19) принимает вид: Ax By D 0 и определяет плоскость параллельную оси OZ . Слу-
чаи, когда A 0 или B 0, аналогичны, и уравнение определяет плос-
кость, параллельную соответствующей оси.
3. Если из трех коэффициентов A, B, C два равны нулю, напри-
мер, A B 0 , то уравнение (3.19) принимает вид: Cz D 0 и определяет плоскость, параллельную плоскости XOY (т. е. плоскость, параллельную и оси OX , и оси OY ).
Вектор n( A, B,C) называется нормальным вектором (или нормалью) плоскости (3.19) и проходит перпендикулярно данной плоскости.
57
Уравнение плоскости, проходящей через три точки
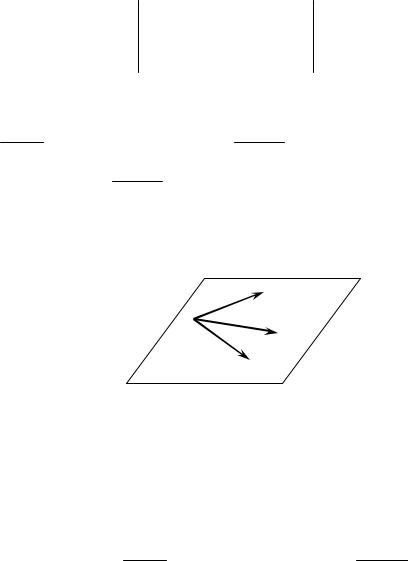
Если даны три точки M1(x1, y1, z1), M 2 (x2 , y2 , z2 ), M3 (x3, y3, z3 ) , не лежащие на одной прямой (рис. 3.7), то уравнение плоскости, про-
ходящей через эти точки, имеет вид:
x x1 x2 x1 x3 x1
y y1 y2 y1 y3 y1
z z1
z2 z1 0 . (3.20) z3 z1
Равенство (3.20) выражает необходимое и достаточное условие компланарности трех векторов:
M1M (x x1, y y1, z z1); M1M 2 (x2 x1, y2 y1, z2 z1);
M1M3 (x3 x1, y3 y1, z3 z1) ,
где M (x, y, z) – любая точка данной плоскости.
|
M2 |
M1 |
M |
|
M3 |
Рис. 3.7
Пример 3.9
Написать уравнение плоскости, проходящей через точки M1(1, 3,2), M2 (8,5;0) и параллельной вектору a(4,1, 1) .
Решение. Пусть точка M (x, y, z) принадлежит искомой плоскости. Тогда векторы M1M (x 1, y 3, z 2), M1M 2 (7,8, 2), a –
компланарны (т. е. их смешанное произведение равно нулю). Тогда получаем:
|
|
|
a |
|
x 1 |
y 3 |
z 2 |
|
|
|
|
|
|
||||
|
|
|
|
7 |
8 |
2 |
|
|
MM1 |
M1M2 |
|||||||
|
|
4 |
1 |
1 |
|
|||
58

(x 1) |
|
8 2 |
|
( y 3) |
|
7 2 |
|
(z 2) |
|
7 8 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 1 |
|
|
|
|
4 1 |
|
|
|
4 1 |
|
|
6x 6 y 3 25z 50 6x y 25z 53. |
|||||||||||||
Приравнивая к нулю полученное смешанное произведение, по- |
|||||||||||||
лучим искомое уравнение |
плоскости: |
|
6x y 25z 53 0 или |
||||||||||
6x y 25z 53 0. |
|
|
|
|
|
|
|
|
|
||||
Уравнение плоскости, проходящей через данную точку и имеющую данную нормаль
Пусть известно, что плоскость проходит через точку M (x0 , y0 , z0 ) иимеетнормаль n( A, B,C) . Тогдаееуравнениеимеетвид:
A(x x0 ) B( y yo ) C(z z0 ) 0. |
(3.21) |
Пример 3.10
Написать уравнение плоскости, проходящей через точки
A(3, 3,0), B(0,7,1),C( 5,3,2) .
Решение. В соответствии с формулой (3.20) имеем
x 3 |
y 3 |
z 0 |
|
(x 3) |
|
10 |
1 |
|
( y 3) |
|
3 |
1 |
|
z |
|
3 |
10 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||
0 3 |
7 3 |
1 0 |
|
|
|
|
|
|
|
|||||||||
5 3 |
3 3 |
2 0 |
|
|
|
6 |
2 |
|
|
|
8 |
2 |
|
|
|
8 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14x 42 2 y 6 62z 14x 2 y 62z 48 0 .
Итак, 7x y 31z 24 0 – искомая плоскость.
Взаимное расположение двух плоскостей
Даны две плоскости: |
|
|
|
||
A1x B1 y C1z D1 0, A2 x B2 y C2 z D2 0. |
(3.22) |
||||
Необходимое и достаточное условие параллельности этих плос- |
|||||
костей выражается равенствами: |
|
|
|
||
|
A2 |
|
B2 |
C2 , |
(3.23) |
|
|
||||
|
A |
B |
C |
|
|
1 |
|
1 |
1 |
|
|
Это означает коллинеарность нормальных векторов n1(A1, B1,C1) и n2 (A2 , B2 ,C2 ) плоскостей (3.22).
59

Косинус угла между плоскостями (3.22) определяется формулой
cos |
|
A1A2 B1B2 C1C2 |
|
|
. |
(3.24) |
|||
A 2 |
B 2 |
C 2 |
A |
2 B |
2 |
C 2 |
|||
|
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
Фактически эта формула определяет угол между нормальными векторами плоскостей. Тогда необходимое и достаточное условие перпендикулярности плоскостей (3.22) выражается равенством
|
|
|
A1A2 |
B1B2 C1C2 0. |
(3.25) |
Нормальное уравнение плоскости. |
|
||||
Расстояние от точки до плоскости |
|
||||
Если вектор |
|
0 {A0 ,B0 |
,C0}, перпендикулярный плоскости |
|
|
n |
|
||||
|
|
A0 x B0 y C0 z D0 0, |
(3.26) |
||
единичный, т. е. A2 |
B2 |
C2 |
1, то уравнение плоскости (3.26) в этом |
||
0 |
0 |
0 |
|
|
|
случае называется уравнением в нормальном виде. Если плоскость дана
в общем виде Ax By Cz D 0, |
то его можно привести к нормально- |
||||||||
му виду, разделив обе части этого уравнения на | n | |
A2 B2 C 2 . |
||||||||
В этом случае мы получим нормальное уравнение плоскости: |
|||||||||
|
Ax By Cz D 0. |
|
(3.27) |
||||||
|
|
|
A2 B2 C2 |
|
|
||||
Расстояние |
от |
точки |
M0 (x0 , y0 , z0 ) |
до |
плоскости |
||||
Ax By Cz D 0 вычисляется по формуле |
|
|
|||||||
|
d |
|
Ax0 By0 Cz0 D |
|
|
. |
|
(3.28) |
|
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|||
|
|
|
A2 B2 C2 |
|
|
||||
§3.6. Различные виды уравнений прямой
впространстве
Пусть дана точка M 0 (x0 , y0 , z0 ) на прямой и направляющий вектор a {a1, a2 , a3}. Этими условиями вполне определяется положение прямой в пространстве. Возьмем на прямой текущую точку M (x, y, z) . Векторы M0M и a коллинеарны. Следовательно, имеетместоравенство
M0M = a t.
60
