
Математика / 4015
.pdfA |
|
1 3 |
|
1, |
|
A |
|
2 |
|
3 |
|
1, |
A |
|
2 |
1 |
|
1. |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
31 |
|
3 |
10 |
|
|
|
|
|
|
32 |
|
7 |
10 |
|
|
|
|
33 |
|
7 |
3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
0 2 1 |
|
0 2 1 |
|
|
|||||||||||||
|
|
|
|
A |
1 |
|
|
|
|
|
|
|
|
|
10 5 1 |
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
10 5 1 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
3 3 1 |
|
3 3 1 |
|
|
|||||||||||||
Легко проверить, что AA 1 = |
A 1 A = E. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Возьмем систему следующего вида: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
a11x1 a12x2 a1n b1, |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21x1 a22x2 a2n xn b2 , |
|
|
|
|
(2.1) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1x1 an2 x2 annxn bn. |
|
|
|
|
|
|||||||||||||||||
Систему (2.1) n линейных уравнений с n неизвестными можно |
|||||||||||||||||||||||||||||
записать в матричном виде AX = B, где |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
a a |
|
a |
|
|
|
|
|
x |
|
|
|
b |
|
|||||||||||||
|
|
|
|
|
11 |
|
|
12 |
|
|
1n |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|||||
|
|
|
a21 a22 |
a2n |
|
|
|
X |
|
x2 |
|
|
|
b2 |
|
||||||||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
, |
|
B |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
a |
n1 |
|
a |
n2 |
a |
nn |
|
|
|
|
|
x |
n |
|
|
|
b |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||||||||
Если система является невырожденной, т. е. detA 0, то она имеет единственное решение:
|
|
X = A 1B, |
(2.2) |
|||
где A 1 – матрица, обратная матрице A. |
|
|
||||
Пример 2.20 |
|
|
|
|
|
|
Решить систему уравнений: |
|
|
|
|
||
|
4x |
3x |
2 |
2x |
3 |
9, |
|
1 |
|
|
|
||
|
2x1 5x2 3x3 4, |
|||||
|
|
|
|
2x3 |
18. |
|
5x1 6x2 |
||||||
41
Решение. Данную систему запишем в матричном виде AX = B,
где
4 3 2 |
|
x |
|
9 |
|
||||
|
2 |
5 |
3 |
|
1 |
|
|
4 |
|
A |
, |
X x2 |
, |
B |
. |
||||
|
5 |
6 |
2 |
|
x |
|
18 |
|
|
|
|
|
|
|
3 |
|
|
|
|
Вычислим определитель матрицы A и найдем матрицу A–1:
|
|
4 |
3 |
2 |
|
|
|
||||
|
|
2 |
5 |
3 |
39, |
|
|
5 |
6 |
2 |
|
A11 8, A12 11, A13 13, A21 6, A22 18,
A23 39, A31 1, A32 16, A33 26,
|
|
|
1 |
|
8 |
6 |
1 |
|
A |
1 |
|
|
11 |
18 |
16 |
|
|
|
|
|
|
|||||
|
39 |
|||||||
|
|
|
|
13 |
39 |
26 |
|
|
|
|
|
|
|
|
|||
По формуле (2.2) получаем решение системы: |
|
|
|
|
||||||||||||
|
1 |
|
8 |
6 |
1 9 |
|
|
1 |
78 |
|
|
2 |
|
|||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
11 |
18 |
16 |
4 |
|
|
|
117 |
|
|
3 |
|
, |
||
39 |
39 |
|||||||||||||||
|
|
13 |
39 |
26 |
|
|
|
|
|
|
5 |
|
|
|||
|
|
|
18 |
|
|
|
195 |
|
|
|
|
|||||
т. е. x1 2, x2 3, x3 5.
§ 2.5. Системы линейных однородных уравнений
Система линейных однородных уравнений имеет вид:
a11x1 a12 x2 a1n xn 0,
a21x1 a22 x2 a2n xn 0,
an1x1 an2 x2 ann xn 0.
Очевидно, что система линейных однородных уравнений всегда имеет нулевое решение, т. е. решение вида x1 x2 xn 0. Это
42
решение не представляет интереса. Нас интересует ответ на вопрос, при каких условиях однородная система имеет ненулевое решение. На это отвечает следующая теорема: система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда определитель матрицы системы равен нулю. Последнее означает, что одно или несколько уравнений системы можно получить из оставшихся путем линейных преобразований. Говорят еще, что такие уравнения линейно зависимы.
Ограничимся рассмотрением только двух разновидностей таких систем:
1)система двух уравнений с двумя неизвестными;
2)система трех уравнений с тремя неизвестными. Случай 1. Два уравнения с двумя неизвестными.
Пример 2.21
Решить систему линейных однородных уравнений:
3x 4 y 0,
x 2 y 0.
Очевидно, что |
|
3 |
4 |
|
0 . Система имеет только нулевое ре- |
|
|
||||
|
|
1 |
2 |
|
|
шение x y 0 .
Пример 2.22
Решить систему линейных однородных уравнений:
x |
3y 0, |
|
|||||
|
|
|
|
|
|
|
|
2x 6 y 0; |
|||||||
|
|
|
1 |
3 |
|
|
0. |
|
|
||||||
|
|
|
2 |
6 |
|
|
|
Равенство нулю определителя матрицы системы означает, что одно уравнение является следствием второго. Например, разделив второе уравнение на (–2), получим первое уравнение. Значит, прямые совпадают. Система имеет бесконечное множество решений, которые можно записать в виде: 3y; y, y R .
Случай 2. Три уравнения с тремя неизвестными.
Здесь возможны три ситуации. Три плоскости могут иметь одну общую точку (0, 0, 0), т. е. это нулевое решение. Три плоскости могут совпадать – это в том случае, когда каждое из трех уравнений являет-
43
ся следствием любого другого. То есть мы имеем дело с тремя одинаковыми уравнениями. Наконец, три плоскости могут пересекаться по прямой. В этом случае одно из уравнений является линейной комбинацией двух остальных уравнений.
Пример 2.23
Решить систему линейных однородных уравнений:
2x 3y 5z 0,
x 4 y z 0,3x 7 y 6z 0.
|
|
2 3 5 |
1 4 1 |
1 4 1 |
|
1 4 1 |
||||||
|
|
|
|
2 |
3 5 |
|
|
0 5 3 |
|
|
0 5 3 |
|
|
|
1 4 1 |
|
|
|
|
|
|||||
|
|
|
|
3 |
7 6 |
|
|
0 5 3 |
|
|
0 0 0 |
|
|
|
3 7 6 |
|
|
|
|
|
|
||||
|
Из второго уравнения имеем y 3 z . |
Из первого уравнения |
||||||||||
|
17 z . Заменив Z на t, |
|
|
|
5 |
|
|
|
|
|||
x |
получим параметрические уравнения пря- |
|||||||||||
|
5 |
|
z t , где t R . |
|
|
|
|
|
|
|||
мой: x 3,4t; y 0,6t; |
|
|
|
|
|
|
||||||
44

Глава 3 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Декартова прямоугольная система координат в пространстве
определяется заданием линейной единицы для измерения длин и трех пересекающихся в одной точке взаимно перпендикулярных осей, пронумерованных в каком-либо порядке.
M z |
z |
|
|
|
M |
O |
M y |
M x |
y |
|
x
Рис. 3.1
Точка пересечения осей называется началом координат, а сами оси – осями координат. Первая координатная ось называется осью абсцисс, вторая – осью ординат, третья – осью аппликат. Начало ко-
ординат обозначается буквой O, оси координат обозначаются соответственно символами Ox, Oy, Oz (рис. 3.1).
Координатами точки M в заданной системе называются числа: x OM x , y OM y , z OM z ,
где OM x , OM y , OM z – соответственно абсцисса, ордината и апплика-
та точки M; символ M(x, y, z) обозначает, что точка M имеет координаты x, y, z.
§ 3.1. Разложение вектора по трем некомпланарным направлениям
Три вектора a, b, c называются некомпланарными, если не существует такой плоскости, которой эти три вектора параллельны. Если же такая плоскость существует, то векторы a, b, c называются
компланарными.
45
|
|
D |
B |
|
|
|
|
c |
|
B1 |
A1 |
b |
|
||
A |
|
|
|
a |
|
|
|
|
|
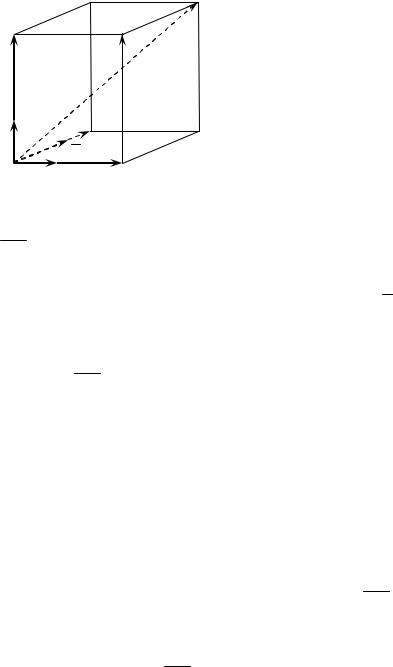
Рис. 3.2 |
|
Любой вектор AB можно разложить по направлениям трех некомпланарных векторов a, b, c, т. е. представить вектор AB в виде
суммы трех векторов, соответственно коллинеарных векторам a, b, c, причем такое разложение является единственным.
Совместим начала векторов a, b, c в точку A и рассмотрим парал-
лелепипед, у которого вектор AB является диагональю (рис. 3.2). Тогда получим
|
|
|
= |
|
|
|
|
|
|
|
|
. |
|
|
|
||
|
AB |
AA1 |
A1D |
DB |
|
|
|
||||||||||
Отсюда |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
AB |
= pa qb |
rc. |
(3.1) |
||||||||||||
Легко доказать, что вектор |
|
разложен по векторам |
a, |
|
, c |
||||||||||||
AB |
b |
||||||||||||||||
единственным образом.
Пусть x, y, z есть численные значения проекций вектора AB соответственно на оси Ox, Oy, Oz. Эти числа называются координатами
вектора. В дальнейшем вектор AB, заданный координатами x, y, z, будем обозначать следующим образом: AB {x, y, z}.
Свойства координат векторов и действия над векторами
вкоординатах. Деление отрезка в данном отношении
1.Равные векторы имеют равные соответствующие координаты. Обратно, если соответствующие координаты двух векторов равны, то
ивекторы равны.
2.Координаты суммы нескольких векторов равны суммам соответствующих координат этих векторов.
46

3.Координаты разности двух векторов равны разностям соответствующих координат этих векторов.
4.Если умножить вектор a на число , то получим вектор b , координаты которого равны соответствующим координатам данного вектора a , умноженным на число .
5.Если два вектора коллинеарны, то их соответствующие координаты пропорциональны, и обратно, если координаты двух векторов пропорциональны, то векторы коллинеарны.
6. Если вектор AB задан координатами начальной точки A(x1, y1, z1) и конечной точки B(x2 , y2 , z2 ) , то его координаты равны
разностямсоответствующихкоординатконечнойиначальнойточек, т. е.
|
|
{x2 x1, y2 |
y1, z2 z1}. |
(3.2) |
|
AB |
|||
Пусть даны точки A(x1, y1, z1) , |
B(x2 , y2 , z2 ) и число |
1. Коор- |
||
динаты точки C(x, y, z), которая делит отрезок AB в отношении , находятся по формулам:
|
x1 x2 |
, |
y1 y2 |
, |
z1 z2 |
. |
|
(3.3) |
|
|
|
|
|
||||||
|
1 |
1 |
1 |
|
|||||
§ 3.2. Скалярное произведение двух векторов |
|||||||||
Скалярным произведением вектора |
a на вектор |
|
называется |
||||||
b |
|||||||||
число, равное произведению их длин на косинус угла между ними. Обозначается ab или a b (но ни в коем случае нельзя писать a b – т. к. знак «×» используется для обозначения векторного произведения). Согласно определению
a |
|
|
|
a |
|
|
|
|
cos . |
(3.4) |
|
b |
b |
||||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Свойства скалярного произведения
1. Скалярным квадратом вектора a называется скалярное про-
изведение вектора a на себя: a 2 aa |
|
a |
|
|
|
a |
|
cos0 |
|
a |
|
2. |
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
2. |
Свойство переместительности: a |
|
|
|
a. |
|
|
|
|
|
|
|||||||||||||
b |
b |
|
|
|
|
|
|
|||||||||||||||||
3. |
Сочетательность относительно числового |
множителя: |
||||||||||||||||||||||
( a) |
|
|
(ab ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. |
Распределительность |
относительно |
суммы |
векторов: |
||||||||||||||||||||
|
|
) ac ad . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a(c d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
47
Скалярное произведение в координатах
Скалярное произведение двух векторов
a (x1, y1, z1), |
|
(x2 , y2 , z2 ) |
(3.5) |
||
b |
|||||
выражается формулой |
|
||||
a |
|
x1x2 y1 y2 z1z2 , |
(3.6) |
||
b |
|||||
т. е. скалярное произведение двух векторов равно сумме произведений соответствующих координат.
Ортогональность двух векторов. Векторы (3.5) перпендикуляр-
ны тогда и только тогда, когда их скалярное произведение равно ну-
лю, т. е. x1x2 y1 y2 z1z2 0.
Угол между двумя векторами
Косинус угла между векторами (3.5) определяется формулой
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1x2 y1 y2 z1z2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
cos |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
x12 y12 z12 |
|
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
b |
|
|
x2 |
y2 |
z2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Пример 3.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Даны точки |
|
|
|
|
|
A(1;10; 5), B(9;3; 7), C(8; 1;3). |
|
Найти: а) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
AB |
BC; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
б) угол между |
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
; в) площадь треугольника ABC. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
AB |
AC |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение: а) |
|
|
|
|
|
|
|
|
|
|
|
(9 1,3 10, 7 ( 5)) (8, 7, 2). Аналогич- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
AB |
||||||||||||||||||||||||||||||||||||||||||||||||||||
но находим |
|
|
|
( 1, 4,10). |
|
|
|
|
|
8( 1) 7( 4) 2 10 0 |
|
(значит, |
||||||||||||||||||||||||||||||||||||||||||||||
BC |
AB |
BC |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
треугольник ABC прямоугольный, |
B 90o ); |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
б) AC (7, 11, 8). Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
cos A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 7 ( 7)( 11) ( 2)8 |
|
|
|
||||||||||||||||||||||||||||||
AB |
AC |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
AB |
|
AC |
|
|
|
|
|
|
82 ( 7)2 |
( 2)2 |
|
72 ( 11)2 82 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
117 |
|
|
|
|
|
117 |
|
|
|
2 |
, A 45o ; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
117 |
|
|
|
|
|
|
234 |
|
117 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
в) т. к. sin A sin 45o |
|
|
|
2 |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S ABC 1 |
|
AB |
|
|
|
AC |
|
sin A |
1 |
|
117 |
234 |
|
|
2 |
|
117 58,5 кв. ед. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|||||||
48
§ 3.3. Векторное произведение двух векторов
Ориентированные тройки векторов
Пусть дана тройка некомпланарных векторов a, b , c, выходящих
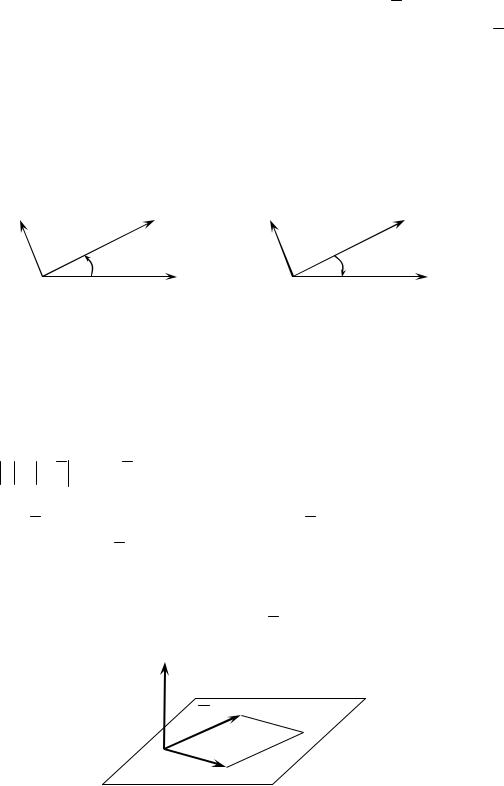
из одной точки. Будем вращать вектор a в плоскости векторов a, b по кратчайшему пути до совмещения его направления с направлением вектора b и будем наблюдать за этим вращением с конца вектора c. Если это вращение будет совершаться против часовой стрелки, то упорядоченная тройка векторов называется правой. Если же вышеуказанное вращение совершается по часовой стрелке, то упорядоченная тройка векторовназываетсялевой(рис. 3.3).
c |
|
|
|
c |
|
|
|
|
|
b |
|
b |
|||||
Правая тройка векторов |
a |
|
|
a |
||||
Левая тройка векторов |
||||||||
|
|
|
|
Рис. 3.3 |
|
|
|
|
|
Векторное произведение |
|
|
|
||||
Векторным произведением векторов a и |
|
называется такой |
||||||
b |
||||||||
третий вектор c, |
который удовлетворяет следующим условиям: |
|||||||
1) c a 
 b sin(a,b );
b sin(a,b );
2) его направление перпендикулярно плоскости, содержащей векторы a ,b , т. е. перпендикулярно и a и b ;
3) векторы a, b , c в указанном порядке образуют такую же
тройку, какую образуют единичные векторы системы координат, например, правую тройку (рис. 3.4).
Обозначается c a b или c [a, b ].
c
b
a
Рис. 3.4
49
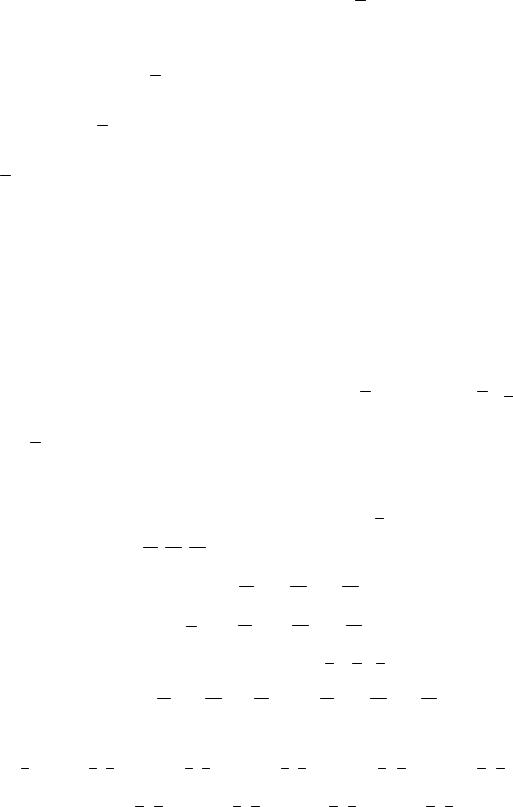
Геометрический смысл векторного произведения
Модуль векторного произведения | a b | численно равен площади параллелограмма, построенного на векторах a, b.
Пример 3.2
Векторы a и b имеют длины, соответственно равные 8 и 5, и
образуют угол в 30о. Найти площадь треугольника, построенного на векторах a и b .
Решение. Площадь параллелограмма, построенного на векторах a, b , равна 8 5sin 30о 40 0,5 20 кв. ед. Значит, площадь соответствующего треугольника равна 20 0,5 10 кв. ед.
Свойства векторного произведения:
1.Векторное произведение равно нулю, если либо по крайней мере один из векторов есть нулевой вектор, либо векторы коллинеарны.
2.При перестановке сомножителей векторное произведение ме-
няет знак на противоположный: a b b a.
3. Свойство распределительности: (a b ) c a c b c.
4. Сочетательность относительно скалярного множителя: ( a) b (a b ).
Векторное произведение двух векторов в координатах
Пусть даны два вектора a (x1, y1, z1) , b (x2 , y2 , z2 ) в правой системе координат e1,e2 ,e3 . Тогда, используя формулу (3.1), получим:
a x1e1 y1e2 z1e3 ; b x2 e1 y2 e2 z2 e3 .
Составим векторное произведение c a b:
c (x1e1 y1e2 z1e3 ) (x2 e1 y2 e2 z2 e3 ).
Пользуясьсвойствами1–4 векторногопроизведения, получим:
cx1 x2 e1 e1 x1 y2 e1 e2 x1 z2 e1 e3 y1 x2 e2 e1 y1 y2 e2 e2
y1 z2 e2 e3 z1 x2 e3 e1 z1 y2 e3 e2 z1 z2 e3 e3 ;
50
