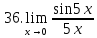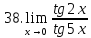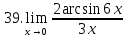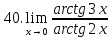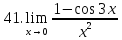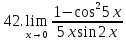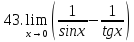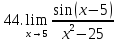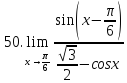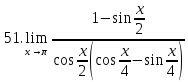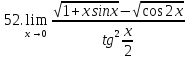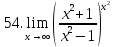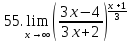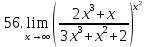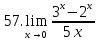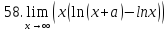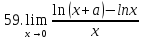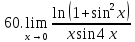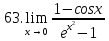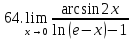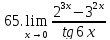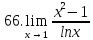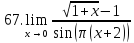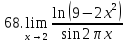Задания
Задание 2.2Вычислить предел функции, используя первый замечательный предел и его следствия.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы:36.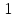 ,37.
,37.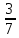 ,38.
,38.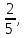 39.
39.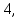 40.
40.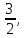 41.
41.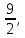 42.
42.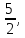 43.
43. 44.
44.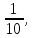 45.
45.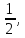 46.
46.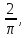
47.
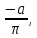 48.
48.
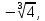 49.
49.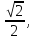 50.
50.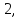 51.
51.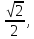 52.
52.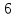 ,
53.
,
53.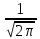 .
.
2.2 Второй замечательный предел.
Вторым замечательным пределом называют предел вида:
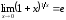 ,
(23)
,
(23)
или эквивалентное выражение
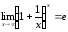 .
(24)
.
(24)
Следствия второго замечательного предела.
1.
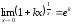
2.
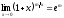
3.

4.
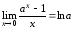
Частный случай:

На основании перечисленных следствий
1-4 и определения эквивалентности
бесконечно малых (18) можно записать
следующие соотношения эквивалентности
при
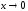 :
:
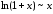 (25)
(25)
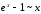 (26)
(26)
 (27)
(27)
Пример 13
Вычислить предел функции
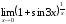 .
.
Решение:
При
подстановке
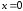 имеем
неопределенность типа
имеем
неопределенность типа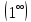 .
.
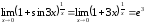 .
.
При решении мы воспользовались соотношением эквивалентности (19) и следствием 1 из второго замечательного предела.
Ответ:
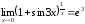
Пример 14
Вычислить предел функции
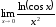
Решение:
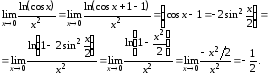
Мы воспользовались соотношениями эквивалентности (19) и (25).
Ответ:
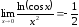
Пример 15
Вычислить
предел функции
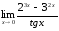
Решение:
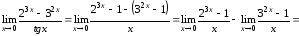
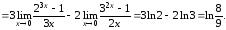
Ответ:
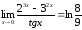
Задания
Задание 2.3Вычислить предел функции, используя второй замечательный предел и его следствия.
|
|
|
|
|
|
|
|
Задание 2.4Вычислить предел функции, используя эквивалентность бесконечно малых величин
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы:54.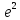 ,55.
,55.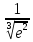 ,56.
,56.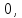 57.
57.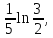 58.
58.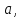 59.
59.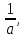 60.
60. 61.
61.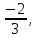 62.
62. 63.
63.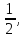 64.
64.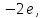 65.
65.
 66.
66.
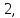 67.
67.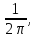 68.
68. 69.
69.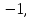 70.
70.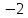 ,
71.
,
71.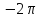 .
.
2.3 Вычисление предела от показательно-степенной функции.
Рассмотрим
теперь показательное степенное выражение
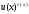 ,
где
,
где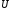 и
и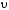 являются функциями одной и той же
переменной
являются функциями одной и той же
переменной .
.
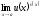 .
(28)
.
(28)
Для
вычисления предела (28)
необходимо вычислить отдельно два
предела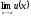 и
и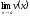 .
Рассмотрим различные случаи, которые
могут возникнуть.
.
Рассмотрим различные случаи, которые
могут возникнуть.
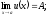
 ,
тогда
,
тогда
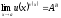 (29)
(29)
Пример 16
Вычислить
предел функции
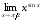
Решение:
Вычислим отдельно пределы основания и показателя степени:
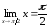 ,
,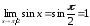 ,
,
поэтому
 .
.
Ответ:
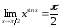
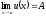 ;
;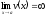 ,
тогда
,
тогда
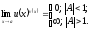
Пример 17
Вычислить предел функции
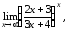
Решение:
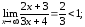
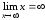 ,
тогда
,
тогда
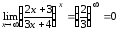 .
.
Ответ: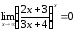
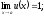
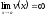 .
.
Искомый предел будет равен
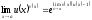 .
.
Пример 18
Вычислить
предел функции


Решение:
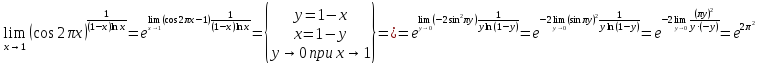
Ответ:
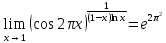
Задания
Задание 2.5Вычислить предел показательно-степенной функции.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы:72. ,73.
,73.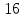 ,74.
,74. 75.
75.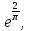 76.
76. 77.
77.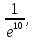 78.
78.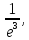 79.
79. 80.
80.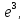 81.
81.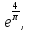 82.
82.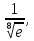 83.
83.
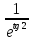 .
.