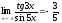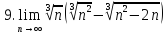Задания
Задание 1.1Вычислить предел числовой последовательности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Ответы:1. ,2.
,2. ,3.
,3. 4.
4. 5.
5. 6.
6. 7.
7. 8.
8.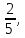 9.
9. 10.
10. 11.
11. 12.
12. 13.
13. 14.
14. 15.
15. 16.
16. 17.
17. .
.
2. Предел функции.
Приведем два определения предела функции:
Определение 4 (по Коши). Число называется пределом функции
называется пределом функции при
при ,
если для любого сколь угодно малого
,
если для любого сколь угодно малого найдется такое
найдется такое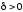 ,
что для всех
,
что для всех удовлетворяющих неравенству
удовлетворяющих неравенству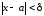 выполняется:
выполняется:
 .
(14)
.
(14)
Определение 5 (по Гейне).Число называется пределом функции
называется пределом функции ,
при стремлении
,
при стремлении к
к ,
если какую бы последовательность
,
если какую бы последовательность с пределом
с пределом ,
извлеченную из множества
,
извлеченную из множества ,
ни пробегала независимая переменная
,
ни пробегала независимая переменная ,
соответствующая последовательность
значений функции
,
соответствующая последовательность
значений функции
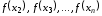 ,...
всегда имеет предел
,...
всегда имеет предел .
.
Обозначают этот факт так:
 .
(15)
.
(15)
Из определения предела функции по Гейне следует, что все теоремы о пределах последовательности можно обобщить на случай предела функции.
Далее приведем несколько примеров вычисления предела функции.
Пример 8
Вычислить предел функции

Решение:
При подстановке в числитель и знаменатель
 мы получаем неопределенность типа
мы получаем неопределенность типа .
.
Выделяем критический множитель
 ,
разложив на множители квадратный
трехчлен в знаменателе и воспользовавшись
формулой разности кубов в числителе.
Затем сократим полученное выражение
на
,
разложив на множители квадратный
трехчлен в знаменателе и воспользовавшись
формулой разности кубов в числителе.
Затем сократим полученное выражение
на .
.

Ответ:

Пример 9
Вычислить предел функции

Решение:
При подстановке
 в предел мы получаем неопределенность
типа
в предел мы получаем неопределенность
типа .
Числитель разложим на множители:
.
Числитель разложим на множители: ;
далее знаменатель и числитель нашей
дроби умножим на величину сопряженную
знаменателю, т.е.
;
далее знаменатель и числитель нашей
дроби умножим на величину сопряженную
знаменателю, т.е.
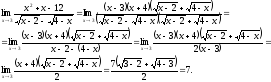
Ответ:

Задания
Задание 2.1Вычислить предел функции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы:18. ,19.
,19. ,20.
,20. 21.
21. 22.
22. 23.
23. 24.
24. 25.
25. 26.
26. 27.
27. 28.
28. 29.
29. 30.
30. 31.
31.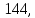 32.
32. 33.
33. 34.
34. ,
35.
,
35. .
.
2.1 Первый замечательный предел.
Первым замечательным пределом называют предел вида:
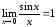 .
(16)
.
(16)
Следствия первого замечательного предела.
1.

2.

3.
4.

5.

6.


7.

Для пределов, содержащих
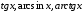 ,
справедливы свойства, аналогичные 4 –
7.
,
справедливы свойства, аналогичные 4 –
7.
Определение 6. Функция называется бесконечно малой при
называется бесконечно малой при ,
если
,
если
 (17)
(17)
Определение 7.Если отношение
бесконечно малых
 стремится к единице при
стремится к единице при :
:
 ,
(18)
,
(18)
то бесконечно малые
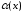 и
и называются эквивалентными бесконечно
малыми,и пишут
называются эквивалентными бесконечно
малыми,и пишут
 при
при .
.
На основании приведенных определений
и первого замечательного предела (16)
можно записать следующие соотношения
эквивалентности при
 :
:
 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
Пример 10
Вычислить предел функции

Решение:
При подстановке
 имеем
неопределенность типа
имеем
неопределенность типа .
.

Здесь
мы воспользовались эквивалентностью
(19)
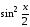 ~
~ при
при .
.
Ответ:

Пример 11
Вычислить
предел функции

Решение:
При подстановке
 имеем
неопределенность типа
имеем
неопределенность типа .
.

Ответ:

Пример 12
Вычислить
предел функции
Решение:
При подстановке
 имеем
неопределенность типа
имеем
неопределенность типа .
.
В данном примере мы не можем применить
первый замечательный предел, так как
 ,
в подобных случаях необходимо сделать
замену переменной. Причем, новая
переменная должна стремиться к нулю.
,
в подобных случаях необходимо сделать
замену переменной. Причем, новая
переменная должна стремиться к нулю.

Ответ: