
Dist_kursPraktikum_4Integral
.pdf
Дистанционный курс «Математика для заочников» 2 семестр
Практикум № 4 «Приложения определенного интеграла»
Площадь плоской фигуры в декартовых координатах.
Пример 1. Вычислить площадь области, ограниченной
графиками функций: |
4 = 8 − , 4 = +6. |
Решение. |
Найдем точки пересечения графиков функций(абсциссы точек пересечения – пределы интегрирования). Для этого решим систему уравнений:
|
|
4 |
= 8 |
− , |
8 − |
|
4 |
= |
+6. |
= +6 , |
|
|
||
− 7 |
+6 = 0, |
7 |
|
|
= 1, |
= |
4 |
|
|
= 6, |
= 3 |
|
|
|
Значит точки пересечения графиков, ограничивающих искомую
площадь, |
1; |
|
, (6;3). Построим эти точки и графики |
|
функций проходящие через них.
Практикум № 4 «Приложения определенного интеграла»

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Искомая |
площадь |
|
равна разности площадей |
||||||||||||||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Площадь |
, |
согласно формуле |
|
|
|
|
|
|
|
|
|
|
|
выражается |
|||||||||||||
= |
|
|
|
|
|
|
= |
|
|
|
|
|
= |
∫ |
|
|
|
|
|
, |
|||||||
интегралом: |
|
1 |
|
(8 − |
) |
|
|
1 |
|
|
|
|
|
|
205 |
|
|||||||||||
= |
= |
|
|
= |
4 |
− |
|
|
|
|
|
|
| = |
. |
|||||||||||||
|
|
3 |
|
|
|||||||||||||||||||||||
Площадь |
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
12 |
|
||||||
|
|
|
трапеции |
|
|
равна произведению полусуммы |
|||||||||||||||||||||
ее оснований на высоту: |
|
+ |
|
|
|
|
|
|
|
|
|
95 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, |
искомая площадь |
|
|
= 8 . |
|
|
|
|
|||||||||||||||||||
|
= |
|
|
2 |
|
|
∙ |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
205 |
95 |
|
5 |
|
|
|
|
|
|
|
|
|
||||||
Ответ: |
|
|
|
= |
− |
= |
12 |
− |
|
8 |
= 5 |
24 |
кв.ед. |
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
Пример52 |
кв.ед. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
. Вычислить площадь области, ограниченную |
|||||||||||||||||||||||||
параболами: |
|
|
= 4 − |
, |
= |
|
|
|
− 2 . |
|
|
|
|
|
|
|
|
|
|||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Определим точки пересечения парабол |
|
= 4 − |
|
, |
= −2 , |
||||||||||||||||||||||
решив уравнение |
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
парабол: |
(−1;3) , |
(2;0). |
|
|
|
|
|
|||||||||||||
Точки пресечения |
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4 − |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Построим эти точки и данные параболы.
Практикум № 4 «Приложения определенного интеграла»

3
Искомую площадь |
можно найти как алгебраическую сумму |
|||||||||||||||||||||||
площадей криволинейных трапеций: |
− |
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
= |
+ |
|
|
|
|
|
|
8 |
|
1 |
|
|||||||||||
= (4 − ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= 4 − |
3 |
| = 8 − |
3 |
+4 − |
3 |
= 9 |
||||||||||||||||||
= ( −2 ) = |
|
|
|
|
− |
| = − |
8 |
+4 = |
4 |
. |
|
|||||||||||||
|
|
|
|
|
||||||||||||||||||||
Площадь |
расположена под осью |
, |
поэтому, чтобы |
|||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
||||||
получить ее величину с положительным знаком, пределы |
|
|||||||||||||||||||||||
интегрирования взяты справа налево. |
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
|||||||||||
= ( −2 |
) = |
|
|
|
|
|
− |
| = |
|
+1 = |
. |
|||||||||||||
3 |
|
|||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
4 |
|
|
3 |
|
|
3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||
=Площадь+ |
− |
|
|
|
|
|
|
= 9+ |
3 |
− |
3 |
= 9. |
|
|
|
|||||||||
Примечание: |
|
|
можно найти иначе, определив ее |
|
||||||||||||||||||||
дифференциал |
как площадь прямоугольника, высота |
|
|
|
||||||||||||||||||||
которого – разность ординат данных парабол, а основание |
, |
|||||||||||||||||||||||
= ( |
− |
) |
= [(4 − |
|
|
) −( |
|
− 2 )] |
= |
|
|
|
||||||||||||
Отсюда |
|
= (4+2 |
|
− 2 |
) . |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
= (4+2 |
−2 |
) |
= (4 |
+ |
− |
|
)| |
= 9. |
|
|
||||||||||||||
Ответ: 9 кв.ед. |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
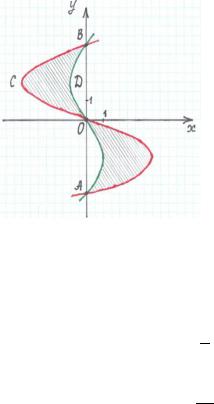
Пример 3. Вычислить площадь области, ограниченную кубическими параболами:
6 = −16 ,24 = − 16
Практикум № 4 «Приложения определенного интеграла»
4
Решение.
Найдем точки пересечения данных парабол:
6 = 24 , |
= 0. |
= 0, = 4, = −4 |
Точки( − 16) = 0, − 16 = 0 , |
||
Построим эти точки и данные(0;0), |
(0;−4), (0;4) |
|
пресечения парабол: |
|
|
параболы.
Искомая площадь |
состоит из двух одинаковых частей; |
||||||
половину ее можно найти как разность площадей |
|
||||||
криволинейных трапеций |
и |
, прилежащих к оси . |
|||||
Тогда по формуле |
= ∫ |
|
1 |
|
имеем: |
|
|
= |
|
= |
|
( |
−16 ) |
; |
|
|
6 |
|
|||||
= |
|
= |
1 |
( |
−16 ) |
; |
|
= 2( |
24 |
||||||
|
|
− |
|
) = |
|
||
Практикум № 4 «Приложения определенного интеграла»

5
= ( − ) = |
1 |
( − 16 ) = |
4 |
=−8 | = (−64+128) = 16 .
Ответ: 16.
Площадь в полярной системе координат.
Пример 4. Вычислить площадь области, ограниченную окружностями:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
= 2√3 |
|
|
|
|
и |
|
|
|
|
|
|
= 2 |
|
|
|
. |
|
|
|
|
|||||||||||
Решив совместно уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
= 2 |
|
|
, |
|||||||||||||
найдем точку пересечения |
окружностей. |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
= 2√3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
|
= 2√3 |
|
|
, |
, |
|
|
|
|
= |
|
, |
√ |
|
|
|
|
, |
|
|
=. |
√3 |
, = |
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
= 2√3 |
∙ |
|
|
|
|
|
|
|
|
|
|
= √3 |
|
|
||||||||||||||||||
= 2√3 |
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Точка пересечения окружностей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
;√3 |
|
|
|
|
|
|||||||||||||||||||||
Построим данные окружности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Искомая площадь |
равна сумме площадей криволинейных |
|
секторов |
и |
. |
Практикум № 4 «Приложения определенного интеграла»
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||
Дуга |
|
|
|
|
|
|
|
описывается концов полярного радиуса |
большей |
||||||||||||||||||||||||||||||||||||||||||||||
от |
до |
, |
|
|
|
|
= 2√3 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
∫ |
|
|
|
|
|
|
|
, имеем: |
||||||||||||||||||||||||
окружности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при изменении полярного угла |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поэтому, по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
= |
|
2 |
|
|
|
|
|
|
|
= |
2 |
|
|
|
|
2√3 |
|
|
= 6 |
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
(1+ |
|
2 |
) = 3 |
|
|
|
(1+ |
|
|
2 |
) |
|
= |
|
|
|
||||||||||||||||||||||
= 3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 (2 ) = 3 |
2 |
+ |
1 |
|
2 | |
2 |
= |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= 3 |
|
2 |
|
− |
3 |
+ |
2 |
|
|
|
|
|
|
|
|
2∙ |
2 |
|
−sin (2∙ |
3 |
) = 3 |
|
6 |
− |
4 |
. |
|||||||||||||||||||||||||||||
Дуга |
|
|
|
|
|
|
|
описывается концом полярного радиуса |
меньшей |
||||||||||||||||||||||||||||||||||||||||||||||
окружности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
до |
|
, поэтому:= 2 |
|
|
|
|
при изменении полярного угла |
|
от 0 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
(2 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
= |
2 |
|
|
|
= |
2 |
|
|
= 2 |
|
|
|
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(1 − 2 ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
|
|
|
(1 − 2 ) = |
|||||||||||||||||||||||||||||||||
Практикум № 4 «Приложения определенного интеграла»
7
|
|
|
1 |
|
2 |
|
1 |
3 |
|
= |
|
− |
2 |
2 (2 ) = |
|
− |
2 |0 |
= |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
√3 |
||
= |
3 |
−0 − |
2 |
2∙ |
3 |
−sin (2∙0) = |
3 |
− |
4 |
. |
|
Следовательно,
|
|
|
= |
+ |
|
|
= |
|
|
|
|
||
|
|
|
√3 |
|
|
|
√3 |
|
5 |
|
|
|
|
= 3 |
|
− |
+ |
|
− |
= |
− √3 . |
||||||
6 |
4 |
3 |
4 |
|
6 |
||||||||
Ответ: 2 56 − √3 кв. ед.
Площадь фигуры, заданной параметрически.
Пример 5. Вычислить площадь области, ограниченную одной аркой циклоиды
|
= |
( − |
), |
|
|
|
|
и осью . |
= |
(1 − |
) |
|
|
|
0 |
Решение. |
(0) = (2 ) |
= 0: |
, |
|
|
|
|
до 2 , так как |
|
в пределах от |
|||||
Арка циклоиды описывается при изменении |
|
||||||
(0) = (1 − 0) = (1− 1) = 0 |
|
, |
> 0 |
|
|
||
а(в2 ) = (1− |
2 ) = (1 −1) = 0 |
|
. |
|
|||
остальных точках указанного промежутка |
|
|
|||||
Практикум № 4 «Приложения определенного интеграла»

8
Пределы интегрирования. |
равны соответственно (0) = 0 и |
(2 ) = 2 |
|
Следовательно, искомая площадь равна:
=.
Пользуясь данными параметрическими уравнениями циклоиды,
преобразуем интеграл к переменной |
; |
= |
|
( − |
|
), |
|
|
|||||||
= (1 − |
) , = (1 − |
] |
). |
|
|
|
, |
|
[0;2 |
] |
|
||||
Когда |
пробегает отрезок |
[0;2 |
|
|
|
|
|
. |
|||||||
|
, |
пробегает отрезок |
|
|
|||||||||||
|
( |
) (= ∫ |
) = ∫ |
( ) |
|
( ) |
|
|
)2 |
|
|
||||
|
2 ( |
|
|
|
|
||||||||||
Поэтому, по формуле |
∙ |
1− |
|
= |
|
|
1− |
|
имеем: |
= |
|
||||
= |
1− |
= |
+ |
) |
|
|
|
|
|
||||||
|
= |
|
(1 −2 |
+ |
= |
= |
|
|
|
|
|||||
|
|
|
− 2 |
|
|
|
|
|
|
|
|
||||
Практикум № 4 «Приложения определенного интеграла»

9
|
= |
|
|
− 2 |
|
+ |
1 |
|
(1 − |
2 ) |
= |
||||
|
3 |
|
|
2 |
|
||||||||||
|
|
= |
|
− |
2 |
− |
1 |
|
|
2 |
(2 ) |
= |
|||
|
|
2 |
|
4 |
|
|
|
||||||||
|
|
|
3 |
|
|
|
|
1 |
|
|
|
||||
|
3 |
= |
|
2 |
| −2 |
| − |
4 |
2 | |
= |
|
|||||
= |
(2 −0)−2( 2 − 0) |
− |
1 |
( 4 − 0) = |
|||||||||||
2 |
|
4 |
|||||||||||||
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
= |
2 |
2 −2(1− 1) − |
4 |
∙0 = 3 |
|
|
|
|
|
|
|
||||
Примечание: так как площадь круга радиуса |
равна |
, то |
|||||||||||||
полученный результат показывает, что площадь арки циклоиды в три раза больше площади круга.
Ответ: 3 кв.ед.
Объем тела вращения.
Пример 6. Вычислить объем тела, образованного вращением области, ограниченной графиками функций:
2 = , 2 +2 −3 = 0 вокруг оси
Решение.
Найдем точки пересечения графиков, для определения пределов интегрирования: + 2 − 3 = 0;
= −3, |
|
= 1, = |
|
, = |
|
. |
||
|
|
|
||||||
−3; |
9 |
, |
1; |
1 |
|
|
|
|
2 |
2 |
|
|
|
|
|||
Практикум № 4 «Приложения определенного интеграла»

10
Построим графики параболы |
= |
|
и прямой |
|
= − .
Ограниченная данными линиями фигура |
при вращении |
|||||||||||||
вокруг оси |
образует тело, объем которого можно найти как |
|||||||||||||
разность объемов тел, образованных вращением вокруг оси |
||||||||||||||
трапеций |
|
и |
. |
|
|
|
|
|
|
|
||||
Объем |
, образованный вращением трапеции |
|
, можно |
|||||||||||
найти по формуле: |
= |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
3 |
|
|
|
|
||||
|
|
|
3 |
|
|
|
|
|
|
|||||
|
= |
) = ( |
= = |
2 |
− |
= |
2 |
− |
= |
|
||||
= |(1,5− |
− 1,5) | = |
( |
−1,5) |
( |
−1,5) = |
|||||||||
( |
− 1,5) |
|
|
[(1 −1,5) |
−(−3 −1,5) |
91 |
|
|||||||
= |
,3 |
| |
= |
3 |
] = |
3 |
. |
|||||||
Объем |
образованный вращением криволинейной трапеции |
|||||||||||||
, найдем по формуле:
Практикум № 4 «Приложения определенного интеграла»
