
Dist_kursPraktikum_4Integral
.pdf
11
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= = |
2 |
= |
4 |
= |
4 |
∙ |
5 |
| = |
|||||||
Искомый |
= |
|
(1 − (−3) ) = |
|
|
(1+243) = |
|
61 |
. |
|||||||||
20 |
20 |
|
|
|
||||||||||||||
|
|
= − = |
− |
= 18 |
|
|
5 . |
|
||||||||||
|
объем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечание: Объем , образованный вращением трапеции , можно найти как объем усеченного конуса по формуле
элементарной геометрии: |
|
|
|
|
|
где |
- |
|||
|
|
|
|
|
||||||
высота усеченного конуса, = (– |
радиусы верхнего и |
|
||||||||
+ ∙ + |
), |
|
||||||||
нижнего оснований. |
, |
|
|
|
|
|
||||
Ответ: |
|
|
куб.ед. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
7. Вычислить объем тела, образованного |
|
|
|||||||
Пример18 |
|
|
|
|
|
|
|
|
|
|
вращением области, ограниченной астроидой: |
|
|
|
|||||||
= |
|
, = |
вокруг оси . |
|
|
|
||||
Решение.
Фигура, ограниченная астроидой симметрична относительно оси .
Практикум № 4 «Приложения определенного интеграла»

|
|
|
|
|
|
|
|
|
|
|
|
12 |
Объем тела вращения вокруг оси |
|
, можно найти по |
||||||||||
формуле: |
= |
|
|
|
= |
|
= 2 |
|
|
|||
|
|
|
|
|
|
|
|
|||||
Исходя из данных параметрических уравнений астроиды |
||||||||||||
= |
|
, = |
= |
, преобразуем последний интеграл к |
||||||||
при |
|
: |
; |
|
; |
= −3 |
∙ |
; |
||||
переменной |
|
|
|
= |
, |
= 0 = |
|
|
, |
|
||
|
= 0, |
= |
|
|
|
|
|
|
||||
|
|
|
|
|
при |
|
|
; |
|
∙ |
, |
|
|
= 2 |
|
|
|
2 |
= |
|
= −3 |
|
= |
||
|
0 |
|
|
|
= 0 , = |
2 |
; = , = 0 |
|||||
|
|
= −6 |
|
|
6 ∙ |
2 ∙ |
. |
|
||||
Далее тождественно преобразуем подынтегральное выражение и, применяя формулу интегрирования степени, получим:
= 2 |
0 |
2 |
|
|
|
=−6 3 |
0 |
∙ |
∙ |
= |
||
|
|
|
2 |
|||||||||
= 6 |
|
|
|
|
|
( 2 )3 ∙ |
|
2 ∙(− |
) |
= |
||
= 6 |
3 |
0( |
1 − |
) |
∙ |
∙(− |
) |
= |
||||
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Практикум № 4 «Приложения определенного интеграла»

13
= 6 |
|
|
2 |
|
(1− 3 |
|
+3 |
|
|
|
|
|
|
|
|
− |
|
) ∙ |
|
|
( |
|
|
|
) = |
|||||||||||||||||||||
|
= 6 |
|
|
( |
|
|
|
|
−3 |
+3 |
|
|
|
|
|
− |
|
|
|
|
) ( |
|
|
|
) = |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
= 6 |
2 |
|
( |
|
|
|
( |
|
|
|
)−3 |
|
|
( |
|
)+ |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
+3 |
2 |
|
|
2 |
|
3 |
( |
|
|
|
|
|
) − |
|
2 |
|
3 |
|
2 |
7 |
( |
1 |
|
)) = |
|
0 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
= |
|
|
3 |
|
|
1 |
|
|
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|||||||||||||||||||
|
6 |
1 |
|
3 |
|
3 |
|
|
− |
5 |
|
|
|
|
|
|
+ |
7 |
|
|
|
|
− |
9 |
|
|
|
| |
|
|
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= 6 |
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
||||||||||||
|
∙( |
3 |
|
|
|
|
|
0 − |
|
|
|
|
|
|
|
2 |
|
− |
5 |
|
|
|
0 − |
|
|
|
|
2 |
|
+ |
||||||||||||||||
|
+ |
3 |
|
|
|
|
|
0− |
|
|
|
|
2 |
|
|
|
− |
|
1 |
|
|
|
|
|
|
0 − |
|
2 |
) = |
|||||||||||||||||
|
|
7 |
|
|
|
|
|
|
1 |
|
|
|
9 |
|
1 |
3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
3 |
|
|
|
|
|
3 |
|
3 |
|
|
32 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
∙ |
3 |
− |
5 |
+ |
7 |
− |
9 |
= |
105 |
|
. |
|
|
|
|
|
|
|||||||||||||||||||
Ответ: куб.ед.
Площадь поверхности вращения.
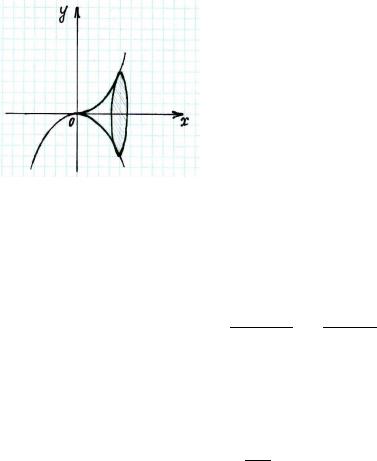
Пример 8. Вычислить площадь поверхности, образованной вращением дуги кубической параболы
Практикум № 4 «Приложения определенного интеграла»
14
= |
|
= 1 |
|
от начала координат до точки с |
|
вокруг оси |
|||
абсциссой |
|
. |
|
|
Решение.
Построим графики функций = и = 1.
Ограниченная данными линиями фигура при вращении вокруг оси образует тело, площадь поверхности которого можно найти по формуле:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
|
∙ 1+( ′) |
|
|
|
|
|
|
|
|
|||||
При этом пределы интегрирования: |
( |
′) |
|
|
|
|
|
|
|||||||||||
Так как |
= |
, |
тогда |
= 3 |
, |
|
|
1+ |
= |
√1+9 |
|
||||||||
|
|
|
|
|
|
|
|
= 0, |
= 1. . |
||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
= |
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= 2 |
|
∙ 1+( ′) |
= |
|
|
|
|
|
|
|||||||||
|
|
|
= 3 |
= |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
= 2 |
|
∙ |
1+9 |
|
|
= 2 |
|
|
∙ |
1+9 |
|
= |
|||||||
|
|
|
|
4 |
|
||||||||||||||
Практикум № 4 «Приложения определенного интеграла»
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
15 |
|||||
|
|
|
|
|
(1+9 ) |
|
|
(1+9 ) = |
|
|
∙ (1+9 |
) |
|
|
|
||||||||||||
= |
2∙9 |
|
|
2∙9 |
∙ |
3 |
|
|
| = |
||||||||||||||||||
= |
|
|
|
∙ |
|
|
|
1+9∙ |
(1 |
) |
−кв. |
√1+0 |
|
= |
|
|
10∙ |
√10 |
−1 . |
||||||||
27 |
27 |
||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
10∙√10 |
−1 |
ед. |
|
|
|
|
|
|
|
|||||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
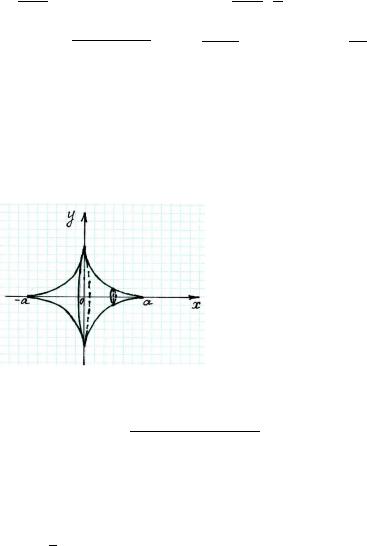
Пример 9. Вычислить площадь поверхности, |
|
|
|
|
|
||||||||||||||||||||||
образованной вращением астроиды: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
|
, = |
|
|
|
|
|
вокруг оси . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение.
Астроида симметрична относительно оси , поверхность тела вращения состоит из двух одинаковых частей, поэтому площадь можно найти по формуле:
= 2∙2 ∫ |
( ) |
, |
( ) |
|
+ |
( ) |
∙ , |
|
Так как |
= |
|
= |
) |
( |
= −3 |
||
|
∙ |
( |
|
, тогда) |
|
|||
′ = 3 |
|
|
|
|
|
|
|
|
Следовательно, учитывая, что четвертая часть астроиды, расположенная в первом квадранте получается при изменении от 0 до ,
Практикум № 4 «Приложения определенного интеграла»

= 2∙2 |
|
|
|
(−3 |
|
)2 + (3 |
|
)2 |
16 |
|||||||||||||
|
|
3 |
2 |
2 |
= |
|||||||||||||||||
|
|
|||||||||||||||||||||
= 4 |
|
2 |
|
|
|
|
∙ |
9 |
|
∙ |
|
+9 |
|
|
|
∙ |
|
|
|
= |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= 4 |
|
|
|
|
|
∙ |
9 |
|
∙ |
|
|
∙( |
+ |
|
) |
= |
|
|||||
= 4 |
|
|
|
2 |
|
∙ |
∙ |
|
= 12 |
|
|
2 |
|
∙ |
= |
|||||||
∙3 |
|
|
|
|
|
|
||||||||||||||||
= 12 |
|
|
2 |
|
|
|
( |
) = |
125 |
∙ |
| |
2 |
= |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
= |
5 |
|
|
|
|
|
2 |
− |
0 = |
5 |
. |
|
|
|
|
|
|
|
|
|
||
Ответ: |
|
|
кв.ед. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Вычисление длины дуги плоской кривой.
Пример 10. Найти периметр фигуры, ограниченной
|
|
|
Решение. |
= и = √2 − |
|
кривыми |
|
|
Найдем точки пересечения кривых: = √2− , = ; = 2 − , = 2 − , + −2 = 0,
Практикум № 4 «Приложения определенного интеграла»

17
|
|
|
−1+ |
−1 = 0, |
||
|
( −1)( + +1) +( − 1)( +1) = 0 |
|||||
|
( |
− 1)( |
+ |
+1+ +1) = 0, |
||
|
|
( − 1)( |
|
+2 |
+2) = 0, |
|
|
( −1) = 0,( |
+2 +2) = 0, |
||||
Точки |
|
= 1, |
|
= 1, |
= −1, = 1. |
|
проходящие через них(1;1) |
и |
(−1;1) |
||||
|
пересечения |
|
|
. Построив эти точки и |
||
данные кривые, получим фигуру, симметричную относительно оси .
Периметр этой фигуры |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||
Пользуясь формулой |
длины дуги |
+ |
|
) |
|
|
|
|
|
|
|
||||||||||||
|
= 2( |
|
|
|
|
|
|
|
|
|
|
||||||||||||
= ∫ |
1+( ′) |
|
|
= ∫ |
|
|
1+( ′) |
|
|
, найдем: |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
= |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
= |
|
1+( ′) = |
|
′ |
|
3 |
|
1 |
= 1+ |
2 |
|
= |
|||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
9 |
|
|
|
4 |
2 |
|
9 |
|
|
|
|
9 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
1+ |
4 |
|
|
= |
9 |
|
|
|
1+ |
4 |
1+ |
4 |
|
= |
|
|||||||
Практикум № 4 «Приложения определенного интеграла»

18
|
|
|
8 |
|
9 |
|
|
|
|
|
|
8 |
|
|
|
9 |
|
|
|
|
−(1+0) |
|
|
|
||||||||||||
|
|
|
= |
27 |
|
1+ |
4 |
|
|
| |
= |
27 |
1+ |
4 |
|
∙1 |
|
|
|
|
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
8 |
13√13 |
−1 ; |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+( ′) |
|
|
|
|
|
|
= |
|
|
2− 2 |
, |
|
|
|
|
||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= ′= |
|
|
2− 2 |
= |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2− |
+ |
|
|
|
|
|
|||
|
|
|
= |
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
||||||||||
|
|
|
|
|
|
|
2− |
2 |
|
|
|
|
|
|
|
|
|
2− |
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
= √2 |
|
|
|
|
|
|
= √2 |
|
|
|
|
| |
= √2 |
|
|
|
|
−0 |
= |
|||||||||||||||||
√2− |
|
|
|
√2 |
|
|
|
√2 |
||||||||||||||||||||||||||||
√2 = 4 .
(Это восьмая часть окружности, радиус которой √2).
Следовательно, искомый периметр фигуры
|
|
|
|
|
|
|
|
|
= 2 |
13√13 − 8 |
+ |
√2 |
≈ 5,102. |
||||
Ответ: |
27 |
|
|
4 |
|
|
||
|
|
5,102 |
|
|
|
|
||
Пример 11. Вычислить длину дуги кривой:
= ∙ ,
=∙
от = 0 до = .
Решение.
Дифференцируя по параметрические уравнения кривой, получим:
Практикум № 4 «Приложения определенного интеграла»
|
|
|
|
|
|
= |
|
|
∙ |
+ |
|
∙ |
|
|
|
= |
|
( |
|
|
+ |
|
|
|
|
19 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
), |
|
|||||||||||||||||
Пользуясь |
= |
|
|
∙ |
|
− |
|
∙ |
|
|
|
= |
|
( |
|
|
− |
|
|
). |
|
||||||||||||||||
|
|
|
|
|
|
формулой для нахождения длины дуги в |
|
|
|
|
|||||||||||||||||||||||||||
параметрическом виде |
= |
∫ |
( |
|
( )) |
+ |
|
|
( ) |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
, |
|
||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
( |
( |
|
|
+ |
|
) |
) + |
( |
|
|
|
− |
) |
|
= |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
|
|
|
( |
|
|
|
|
+2 |
|
|
+ |
|
|
|
+ |
|
|
|
− 2 |
|
|
|
+ |
) |
= |
||||||||||
= |
|
|
|
2 ∙2 |
= |
|
|
|
2 |
∙ |
|
|
|
= |
2 |
∙ | |
|
= |
2 |
|
|
|
|
|
− 0 = |
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Ответ: |
√ |
2 |
|
|
−1 . |
= |
2 |
|
|
|
−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Задачи для самостоятельного решения:
Задача 1. Вычислить площадь области, ограниченную параболой = +4 и прямой − +4 = 0.
Ответ: .
Задача 2. Вычислить площадь области, ограниченную лемнискатой = 2 Ответ:
Задача 3. Вычислить объем тела, образованного
Практикум № 4 «Приложения определенного интеграла»

|
|
|
|
|
|
|
|
|
|
|
20 |
||
вращением области, ограниченной линиями: |
|
|
|
||||||||||
= 2 |
|
, = вокруг оси |
|
|
|
|
|
|
|
||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
||
Задача 4. Вычислить. |
площадь поверхности, образованной |
||||||||||||
вращением дуги кубической параболы |
= |
|
вокруг оси |
||||||||||
, заключенной между прямыми |
|
и |
|
|
|
||||||||
= − |
|
= |
|
|
|||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
Задача 5. |
Вычислить длину дуги кривой |
|
|
|
|
|
|
||||||
|
|
− 1 . |
|
|
2 |
= −2 |
|||||||
между точками пересечения с осью |
. |
||||||||||||
Ответ: √6+ln √2+√3 .
Практикум № 4 «Приложения определенного интеграла»
