
Задачи.
В задачах 1.17.-1.22. доказать справедливость следующих тождеств:
1.17. А + А = А, АА = А, А + Ø = А, АØ = Ø , АΩ = А, А + Ω = Ω.
1.18.
![]()
![]() =Ø,
┐Ø
= Ω,
=Ø,
┐Ø
= Ω,![]() Ø.
Ø.
1.19.
а)
![]() (правила
де Моргана), б) Обобщить правила де
Моргана на произвольное число п
событий.
(правила
де Моргана), б) Обобщить правила де
Моргана на произвольное число п
событий.
1.20**. АВ + С = (А + С)(В + С) (дистрибутивность сложения относительно умножения).
1.21.
![]() .
.
1.22*.
(А
+ В) - В = А - АВ =
![]() =
А
- В.
=
А
- В.
Замечание. Этот пример показывает, что «приведение подобных членов» в алгебре событий недопустимо.
1.23. Пусть А, В и С—события, наблюдаемые в эксперименте причем А и В несовместны. Показать, что события АС и ВС также несовместны.
1.24. Показать, что:
а) если
А
![]() В,то
выполняются соотношения АВ
= А, А + В = В; (**)
В,то
выполняются соотношения АВ
= А, А + В = В; (**)
б) из
справедливости любого из соотношений
(**) следует А
![]() В.
В.
1.25. Пусть А и В — наблюдаемые события в эксперименте. Показать, что событие А + В можно разложить на сумму несовместных событий следующими способами:
а)
А + В = А+(В
- АВ);б)
![]() ;в)
;в)
![]() .
.
1.26*.
Показать,
что если
![]() ,
то
,
то![]() .
.
1.27.
Показать,
что если![]() ,
то
(А
- В)
+
В
= А.
,
то
(А
- В)
+
В
= А.
Доказать тождества:
1.28.
![]() .
.
1.29.
![]() .
.
1.30.
![]() .
.
1.31*. АС-В = АС- ВС.
1.32*. (А - В) + (А - С) = А - ВС.
Симметрическая разность двух событий А∆В определяется следующим образом:
А∆В=(А - В) + (В - А).
Доказать следующие тождества:
1.33. А∆В = (А + B) - АВ.
1.34.![]() .
.
1.35.
![]() .
.
1.36. Пусть С = А∆В. Доказать, что А∆С = В.
1.37.
Найти случайное событие X
из
равенства
![]()
1.38**.
Доказать,
что А
—
В
= Ø
тогда и только тогда, когда А
![]() В.
В.
1.39*.
Очередной
посетитель входит в зал музея, где уже
собралось 2n
человек, и начинает отыскивать знакомых
среди собравшихся. Интересующие нас
события: А
=
{среди собравшихся найдется п
человек,
знакомых посетителю}, В
=
{среди собравшихся найдется п
человек,
не знакомых посетителю}. Доказать,
что события А
+ В и
![]() достоверные.
достоверные.
Пусть А, В, С — три события, наблюдаемые в данном эксперименте. В задачах 1.40.-1.42. выразить указанные события в алгебре событий.
1.40. Е1 = {из трех событий А, В, С произойдет ровно одно}, F1 = {из трех событий А, В, С произойдет ровно два}.
1.41. Е2 = {из трех событий А, В, С произойдет хотя бы одно}, F2 = {из трех событий А, В, С произойдет не меньше двух}.
1.42. Е3 = {из трех событий А, В, С не произойдет ни одного}, F3 = {из трех событий А, В, С произойдет хотя бы два}, G = {из трех событий А, В, С не произойдет хотя бы одно}.
1.43. Поражение боевого самолета может наступить или в результате поражения обоих двигателей (события D1 и D2), или в результате попадания в кабину пилота (событие К). Производится длительный обстрел самолета из зенитного орудия. Любое попадание в соответствующий агрегат приводит к его поражению. Пусть событие А = {поражение самолета}.
а) Описать множество элементарных исходов.
б) Записать А в алгебре событий как непосредственно с помощью событий D1, D2 и К, так и через элементарные исходы.
в)** Получить из второй записи первую путем допустимых алгебраических преобразований.
1.43. Электрическая цепь составлена по схеме, приведенной на рис. 1.10 Событие Ak = {элемент с номером k вышел из строя}, k = 1, 2, 3, 4. Событие В = {разрыв цепи}. Выразить событие В в алгебре событий А1, А2, А3, А4.

рис. 1.10
1.44. Электрическая цепь составлена по схеме, приведенной на рис. 1.11 Событие Ak = {элемент с номером k вышел из строя}, k = 1, 2, 3, 4, 5. Событие В = {разрыв цепи}. Выразить событие В в алгебре событий А1, А2, А3, А4, А5.
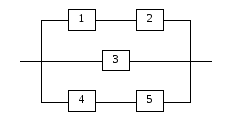
рис. 1.11
1.45. На отрезке [а, b] наудачу ставятся две точки. Пусть х и y - координаты этих точек. Изобразить на плоскости Оху области, соответствующие событиям Ω, А, В, АВ, А- В, А + В, где А = {вторая точка ближе к левому концу отрезка, чем первая точка к правому концу}, В = {расстояние между точками меньше половины длины отрезка}.
1.46. Произведено
три выстрела из орудия по цели. Событие
Ak![]() =
{попадание при k-м
выстреле}
(k
= 1, 2, 3).
=
{попадание при k-м
выстреле}
(k
= 1, 2, 3).
а)
Выяснить состав множества Ω,
выразив
каждый элементарный исход
![]() через
событияAk.
через
событияAk.
б) Записать в алгебре событий следующие события:
А = {ровно одно попадание}, В = {хотя бы одно попадание}, С = {хотя бы один промах}, D = {не меньше двух попаданий}, Е = {попадание не раньше, чем при третьем выстреле}.
1.47. Из
ящика, содержащего 10 деталей, из которых
3 бракованных, наудачу последовательно
и без возвращения извлекается
по одной
детали до появления бракованной, после
чего опыт пре
кращается. Обозначим
исход i-го
испытания
![]() = {бракованная
деталь
появится при i-м
испытании}. Рассмотрим событие А
=
=
{придется производить третье по счету
извлечение детали}.
= {бракованная
деталь
появится при i-м
испытании}. Рассмотрим событие А
=
=
{придется производить третье по счету
извлечение детали}.
а) Сконструировать
элементарные исходы данного опыта с
помощью алгебраических операций над
исходами![]() ,i
=
1, 2, ...
,i
=
1, 2, ...
б) Записать событие А через элементарные исходы и упростить запись путем алгебраических преобразований.
1.48. Два баскетболиста по очереди бросают мяч в корзину до первого попадания. Выигрывает тот, кто первый забросит мяч. События: Аk = {первый баскетболист попадает при своем k-м броске}, Bk = {второй баскетболист попадает при своем k-м броске}; A = {выигрывает первый баскетболист}, В = {выигрывает второй}. Первый баскетболист бросает первым. Определить состав множества элементарных исходов и записать события А и В в алгебре событий.
1.49. Показать, что совокупность элементарных исходов любого эксперимента с конечным множеством Ω образует разбиение множества Ω.
1.50. Эксперимент состоит в раскладывании наудачу трех занумерованных шаров по трем ящикам. В каждый ящик может поместиться любое число шаров. Наблюдаемый результат – тройка чисел (i, j, k), где i, j, k – номера ящиков, в которые попали соответственно первый, второй и третий шары. События А={первый ящик пустой}, В={в каждый ящик попало по одному шару}, С={все шары попали в один ящик}.Образуют ли события А, В и С полную группу событий?
1.51.
Показать,
что система событий
![]() ,
где
D1,
D2
и
К
—
наблюдаемые события в эксперименте,
описанном в задаче 1.43.,
образует разбиение множества Ω,
для
данного эксперимента.
,
где
D1,
D2
и
К
—
наблюдаемые события в эксперименте,
описанном в задаче 1.43.,
образует разбиение множества Ω,
для
данного эксперимента.
1.52. Множество элементарных исходов некоторого эксперимента состоит из четырех исходов. Сколько различных разбиений можно составить для данного множества?
Пусть
А
—
произвольное наблюдаемое в некотором
эксперименте событие такое, что А
![]() Ωи
А
Ωи
А
![]() Ø.
Показать, что система множеств
Ø.
Показать, что система множеств
![]() образует разбиение множества Ω.
образует разбиение множества Ω.
Пусть Ω = {1, 2, 3, ... } — множество натуральных чисел. Показать, что система {S1, S2, S3}, где S1 = {х | х = 3п; п = 1, 2, 3, ...}, S2 = {x | x =3п - 1; n = 1, 2, 3, .,.}, S3 = { х | х = 3п - 2; п = 1, 2, 3, ... }, образует разбиение множества Ω.
1.53. Для некоторого эксперимента множество Ω содержит ровно п элементарных исходов. Показать, что число всех наблюдаемых событий, содержащихся в поле событий для данного эксперимента, равно 2п.
1.54. Случайным образом выбирают одну из 28 костей домино. Опишите пространство элементарных исходов Ω.
Перечислите все элементарные исходы, из которых состоят следующие события:
а) А – на выбранной кости очки совпадают;
б) В – сумма очков на выбранной кости равна шести;
в) С – произведение очков на кости нечетно;
г) B/A;
д) АВ;
е) АС;
ж) АВ/С;
з) (А
![]() В)
С.
В)
С.
1.55.
По мишени производят три выстрела. Пусть
событие Ai
i
= 1, 2, 3, - попадание при i-м
выстреле. Представьте в виде объединения
и пересечения событий
![]() и
и![]() следующие
события:
следующие
события:
а) А – три попадания в мишень;
б) В – три промаха;
в) С – хотя бы одно попадание;
г) D – хотя бы один промах;
д) E – не менее двух попаданий;
е) F – не больше одного попадания;
ж) G – попадание в мишень не раньше, чем при третьем выстреле.
1.56. Пусть А, В, С – случайные события. Выясните смысл равенств:
а) АВС
= А;
б) А
![]() В
В
![]() С
= А.
С
= А.
1.57.
Пусть А
![]() В. Упростите
выражения:
В. Упростите
выражения:
а) АВ;
б) А
![]() В
= B;
в) АВС;
г) А
В
= B;
в) АВС;
г) А
![]() В
В
![]() С.
С.
1.58. Используя свойства операций над событиями, докажите следующие равенства:
а)
![]() ;
б)
;
б)![]() .
.
1.59. Два игрока играют в шахматы. Событие А – выиграл первый игрок; событие В – выиграл второй игрок. что означают события:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
1.60.
Схема электрической цепи приведена на
рис. 1.12 через участок схемы, вышедши из
строя, ток не проходит. Пусть событие
Ai
– выход из строя элемента i,
i
=
![]() .
Выразите события
.
Выразите события
![]() и
и![]() через события
через события![]() ,
еслиА
– выход из строя всей схемы.
,
еслиА
– выход из строя всей схемы.

рис. 1.12
1.61.
На рис. 1.13 представлена структурная
схема надежности некоторой системы.
Пусть события А
и Аi
означают отказ системы и i
– го элемента соответственно, i
=
![]() .
Выразите события
.
Выразите события
![]() и
и![]() через событияАi
и
через событияАi
и
![]() ,i
=
,i
=
![]() .
.

рис. 1.13
