Решение типовых задач

Задача 1. Бросают две игральные кости. Пусть А – событие, состоящее в том, что сумма очков нечетная; В – событие, заключающееся в том, что хотя бы на одной из костей выпала двойка. Описать события А+В и АВ.

Решение. Сумма А+В представляет собой событие, состоящее в наступлении хотя бы одного из событий А и В. Поэтому А+В означает, что либо сумма выпавших очков будет нечетна, либо на одной из костей выпадет двойка, а на другой – четное число. Произведение АВ представляет собой событие, состоящего в наступлении и события А и события В вместе. Поэтому АВ – событие, состоящее в том, что на одной из костей выпала двойка (событие В), а на второй – нечетное число очков, тога сумма очков – нечетная (событие А).

Задача 2. Доказать, что

(А+В)(А+С)=А+ВС.

Доказательство. Событие (А+В)(А+С) состоит из элементарных событий, которые принадлежат и событию А+В и событию А+С, т.е. это множество элементарных событий, принадлежащих либо событию А, либо событию ВС. Тогда по определению суммы событий имеем

(А+В)(А+С)=А+ВС.

Геометрически событие (А+В)(А+С) представляет собой общую часть областей А+В и А+С (рис. 1.7), а событие А+ВС – объединение областей А и ВС (рис. 1.8), т.е. ту же самую область (А+В)(А+С).

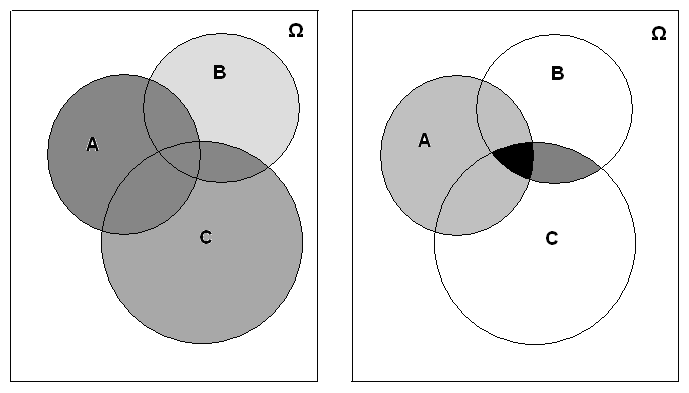
Рис. 1.7 Рис. 1.8

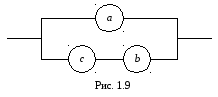
Задача 3. Электрическая цепь, составленная по схеме, приведенной на рис. 1.9. Выход из строя элемента a – событие А, элемента b – событие В, элемента с – событие С.Записать выражение событий и, еслиозначает разрыв цепи.

Решение. Разрыв цепи произойдет в том случае, если выйдет из строя элемент а и хотя бы один из элементов b, c . Эти события соответственно равны А и B+C. Поэтому,

.

Цепь будет замкнута в том случае, если не выйдет из строя элемент а и не выйдут из строя элементы b и c вместе. Эти события соответственно равны и. Следовательно,

Вопросы.

1. Что означают события А+А и АА?

2. Событие А – хотя бы одно из трех изделий бракованное; В – все три изделия доброкачественные. Что означает событие а) А+В; б) АВ?

3. Бросают две игральные кости. Пусть А – событие, состоящее в том, что сумма очков нечетная; В – событие, заключающееся в том, что хотя бы на одной из костей выпала единица. Описать событие .

4. Равносильны ли события А и В, если: 1) А=В; б) А+С=В+С?

5. Пусть А, В, С – три произвольных события. Найти выражения для событий, состоящих в том, что а) произошли все три события; б) произошло хотя бы одно из событий; в) произошли хотя бы два события; г) произошли два и только два события; д) произошло одно событие; е) ни одно событие не произошло; ж)произошло не более двух событий.

6. Из таблицы случайных чисел наудачу взято одно число. Событие А – выбранное число оканчивается нулем, событие В – данное число делится на пять. Что означают события В – А и АВ?

7. Доказать, что для любых событий А, В, С: (А + В) С = АС + ВС.

8. Пусть А, В и С – случайные события. Выяснить смысл равенств: а) АВС = В; б) А + В + С = В.

9. Доказать, что для любых событий А и В имеют место следующие равенства: а) ; б).

10. Когда возможны равенства: а) А + В = А; б) ; в)А +В = АВ; г) АВ = А; д) ?

11. Рабочий обслуживает три автоматических станка. События А – первый станок потребует внимания рабочего в течение часа; В – второй станок потребует внимания рабочего в течение часа; С – третий станок потребует внимания рабочего в течение часа. Что означают события: а) АВС; б) А + В + С; в) ; г); д); е)А + В + С – АВС?

12. Пусть А, В – случайные события. Упростить следующие выражения для событий: а) ; б).

13. Пусть А, В – случайные события, U – достоверное событие. Доказать, что образуют полную группу событий.

14. Пусть А и В – произвольные события. Доказать следующие равенства а) ; б).

15. Для любого числа событий доказать следующие равенства а); б).

16. Доказать, что события: а) и б)достоверны.

17. Доказать, что событие невозможно.

18. Каково условие совместности событий ?

19. Найти случайное событие Х из равенства

.

20. Прибор состоит из трех блоков первого типа и четырех блоков второго типа. Событие А_i (i = 1, 2, 3) – исправен i-й блок первого типа; В_j (j = 1, 2, 3, 4) – исправен j-й блок второго типа. Прибор работает, если исправен хотя бы один блок первого типа и не менее трех блоков второго типа. Найти выражение для события С, которое соответствует работе прибора.