Вариант 19

Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы

Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений

Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов .

1. Доказать, что она является базисом в пространстве , написать матрицу перехода от стандартного базисапространства к базису .

2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора в базисе .

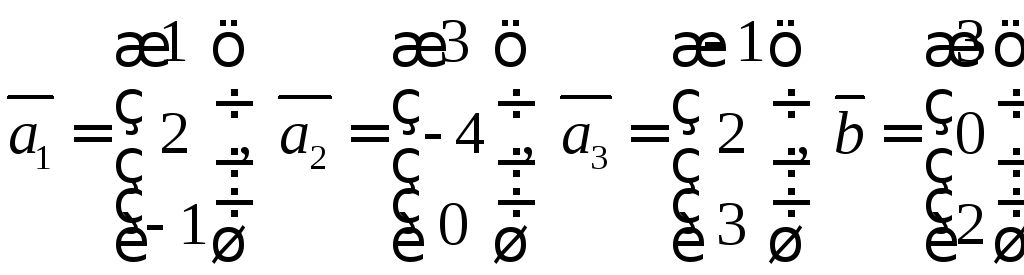
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве вектор-столбцов задан базис. Требуется провести процесс ортогонализации Грама-Шмидта системы векторов базиса, если вскалярное произведение задано в стандартном виде

Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов ,пространстваи дополнить эти векторы до ортогонального базиса

Вариант 20

Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы

Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений

Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов .

1. Доказать, что она является базисом в пространстве , написать матрицу перехода от стандартного базисапространства к базису .

2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора в базисе .

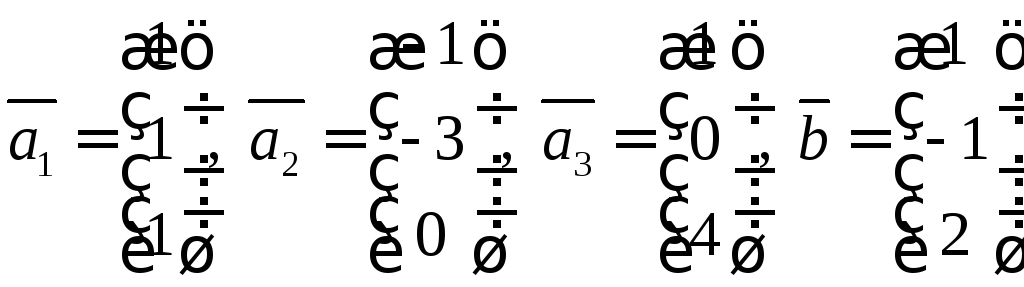
Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве вектор-столбцов задан базис. Требуется провести процесс ортогонализации Грама-Шмидта системы векторов базиса, если вскалярное произведение задано в стандартном виде

Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов ,пространстваи дополнить эти векторы до ортогонального базиса

Вариант 21

Задание 1 (линейная зависимость систем векторов). Исследовать на линейную зависимость систему векторов. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы

Задание 2 (базис и размерность линейного пространства решений ОСЛАУ). Найти базис и размерность линейного пространства решений однородной системы линейных алгебраических уравнений

Задание 3 (формулы преобразования координат при переходе от базиса к базису). Дана система векторов .

1. Доказать, что она является базисом в пространстве , написать матрицу перехода от стандартного базисапространства к базису .

2. Написать формулы преобразования координат при преобразовании базиса. Пользуясь полученными формулами, найти координаты вектора в базисе .

,

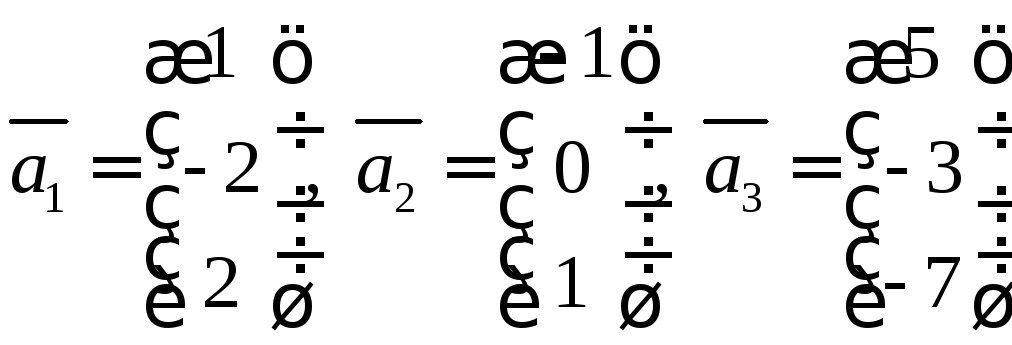Задание 4 (процесс ортогонализации Грама-Шмидта системы векторов). В пространстве вектор-столбцов задан базис. Требуется провести процесс ортогонализации Грама-Шмидта системы векторов базиса, если вскалярное произведение задано в стандартном виде

Задание 5 (дополнение системы векторов до ортогонального базиса). Проверить ортогональность векторов ,пространстваи дополнить эти векторы до ортогонального базиса